ГЛАВА ЧЕТВЕРТАЯ

В свое время почти каждый из нас грезил пиратами и фрегатами. В пылких мечтах мы переживали бои и погони, тайны острова сокровищ и подвиги благородства. Мы видели почти наяву, как по голубому морю, слегка накренившись, фрегаты бесшумно уходят за горизонт, оставляя за кормою пенный след. Иногда, чтобы увеличить скорость парусника, пираты шли на отчаянный шаг: они выбрасывали за борт балласт и лишь благодаря этому благополучно уходили от погони. Зачастую это им сходило с рук, но время от времени они бывали жестоко наказаны: фрегат, лишенный балласта, становился неустойчивым, как яичная скорлупа под парусами, и первый же шквал опрокидывал его вверх дном.

Глава четвертая

Эта глава, пожалуй, самая трудная в книге. На первый взгляд она может показаться настолько сухой и неоправданно сложной, что некоторые читатели сочтут ее ненужным балластом. Но это тот самый балласт, который кладут на дно фрегата, балласт, без которого все паруса нашей фантазии не только бесполезны, но и опасны. Слишком часто в погоне за быстротой и легкостью

Ученье-свет

мы пренебрегаем устойчивостью и глубиной. Однако такая беспечность не остается безнаказанной: в какой-то момент переполненная чаша знаний, лишенная опоры точных фактов, опрокидывается, и все приходится начинать сызнова.

В этой главе нет ничего такого, чего бы не смог понять вдумчивый и неторопливый читатель. Однако она требует некоторых навыков последовательного логического мышления. Как правило, эти минимальные усилия вознаграждаются впоследствии большей полнотой и «объемностью» приобретаемых познаний. Вполне вероятно, что при первом чтении глава вызовет больше вопросов, чем разрешит. Это не беда. Зато она хоть немного позволит заглянуть внутрь «физической кухни», которая обычно скрыта за парадными обедами и здравицами в честь квантовой механики. А главное — лишь после таких экскурсов в глубь новых знаний возникает психологическое ощущение их стройности и устойчивости.

ДО БОРА

К тому времени, когда Нильс Бор появился в лаборатории Резерфорда в Манчестере, об атоме знали уже довольно много. Настолько много, что порой это мешало выделить из груды фактов главные.

На схеме (стр. 78—79) представлены только те из явлений, которые впоследствии оказались действительно основными для понимания структуры атома.

На основании этих фактов (которые наблюдать довольно легко) надо было угадать внутреннее устройство атома — объекта, который никто никогда не видел и не увидит. А у задач подобного типа есть общее название: проблема «черного ящика». Мы знаем характер воздействия на «черный ящик» — атом и результат этого воздействия, то есть знаем, что происходит и отчего. Но мы хотим знать больше: как все происходит, то есть механизм явлений, протекающих в черном ящике. Достигнуть этого значительно труднее, чем восстановить действие в зрительном зале по обрывкам музыки и речи.

Внутренне устройство атома

Даже если мы знаем все внешние проявления внутренних свойств атома, необходимо еще их обобщение, синтез, необходима интуиция, которая через провалы в логических построениях безошибочно приводит к единственно верной картине явлений.

Из нашей далеко не полной схемы видна сложность задачи: необходимо с единой точки зрения (и непротиворечиво) объяснить все эти — очень разные — опыты. Нильс Бор нашел такое объяснение, причем оно оказалось удивительно простым и совершенным по форме.

Это случилось тогда, когда Бору вдруг стало ясно, что три физические идеи: атомы, лучи, электроны — связаны между собой понятием кванта. До сих пор эти идеи развивались независимо. Химия и кинетическая теория материи доказали существование атомов. Электромагнитная теория света Максвелла изучала свойства лучей. Электродинамика Максвелла — Лоренца пыталась осмыслить понятие «электрон».

Атом

Квант действия h, даже после работ Эйнштейна и Милликена, в Европе никто не принимал всерьез, хотя отдельные попытки использовать его были: в 1910 году Артур де Гааз попытался применить соотношение Планка E = hν для определения границ и периодов движения электронов в атоме Томсона; Джон Никльсон в 1912 году пытался использовать идею квантов для анализа спектров Солнца и туманностей, а Вальтер Нернст выдвинул гипотезу о квантовании вращений.

Скептическое отношение к идее квантов лучше всего выразил сам Планк в книге, которую он написал в 1912 году. «Когда подумаешь о полном экспериментальном подтверждении, которое получила электродинамика Максвелла в самых тонких явлениях интерференции, когда подумаешь о невероятных трудностях, которые повлек бы за собой отказ от нее для всей теории электрических и магнитных явлений, то испытываешь какое-то отвращение, когда сразу же разрушаешь эти основы. По этой причине во всем дальнейшем изложении мы оставим в стороне гипотезу квантов света, тем более что ее развитие находится еще в зачаточном состоянии».

АТОМ БОРА

В 1912 году Нильс Бор уже работал в Манчестере у Резерфорда. Манчестер отделен от Европы Ла-Маншем, и, вероятно, поэтому в лаборатории Резерфорда к гипотезе квантов относились хотя и осторожно, но без континентального недоверия. Быть может, поэтому, когда Планк писал свою книгу, Нильс Бор уже был твердо убежден в том, что «...электронное строение атома Резерфорда управляется с помощью кванта действия». Но прошел еще год упорных размышлений, прежде чем он сформулировал свои знаменитые «постулаты Бора».

Как он должен был при этом рассуждать?

Когда Александр Македонский увидел перед собой узел Гордия, то просто разрубил его мечом — он был полководец и победитель. Бору пришлось труднее, но поступил он аналогично. Рассуждал он примерно так: по законам механики, чтобы электрон в планетарном атоме Резерфорда не упал на ядро, он должен вокруг него вращаться. Но по законам электродинамики он обязан при этом излучать энергию и в конце концов все равно упасть на ядро. Нужно запретить ему падать на ядро.

— Позвольте, — возражали ему, — как это — запретить? Между электроном и ядром действуют электрические силы?

— Да, — отвечал Бор.

— Они описываются уравнениями Максвелла?

- Да.

— И даже масса m и заряд е электрона определены из электрических измерений?.

- Да.

— Значит, движение электрона в атоме также должно подчиняться электродинамике Максвелла?

— Нет!

Согласитесь, что такой способ ведения спора может рассердить даже очень спокойного человека. «Но ведь атом все-таки устойчив! — без конца повторял Бор в ответ на все возражения. — И мы не знаем более простой причины этой устойчивости, кроме той, что она есть».

В поисках разумного основания для этого несомненного факта Бор наткнулся на книгу Иоганна Штарка «Принципы атомной динамики» и там впервые увидел формулы Бальмера и Ридберга.

«Мне сразу все стало ясно, — вспоминает Бор. — И после многочисленных попыток использовать квантовые идеи в более строгой форме ранней весной 1913 года мне пришло в голову, что ключом к решению проблемы атомной устойчивости являются изумительно простые законы, определяющие оптический спектр элементов».

Теперь он мог сформулировать свои знаменитые постулаты:

1-й постулат — о стационарных состояниях. В атоме существуют орбиты, вращаясь по которым электрон не излучает.

2-й постулат — о квантовых скачках. Излучение происходит только при перескоке электрона с одной стационарной орбиты на другую. При этом частота излучения ν определяется гипотезой Эйнштейна о квантах света ΔЕ — hν, где ΔЕ — разность энергий уровней, между которыми происходит переход.

Чтобы понять эти постулаты несколько глубже, обратимся к очевидной аналогии между предполагаемым вращением электрона вокруг ядра и вращением спутника вокруг Земли. В свое время Ньютон открыл закон всемирного тяготения, размышляя над вопросом: «Почему Луна не падает на Землю?» Сейчас этот вопрос задают только в старых анекдотах, ибо все знают ответ: «Потому что она движется, причем со строго определенной скоростью, которая зависит от расстояния ее до Земли». Таким образом, чтобы спутник не упал на Землю и в то же время не улетел в космос, между радиусом его орбиты r и скоростью движения по ней v должна существовать определенная связь.

Почему Луна не падает на Землю

В атоме водорода при движении электрона с массой m и зарядом е вокруг ядра атома между скоростью электрона v на орбите и радиусом орбиты r существует аналогичная связь, которую можно записать в виде уравнения: (m v²/2) = (e²/r²).

Это уравнение верно всегда — независимо от того, излучает электрон или не излучает. Оно просто отражает известное равенство центростремительной и притягивающей сил.

Если электрон теряет энергию на излучение (по законам электродинамики), то он упадет на ядро, как спутник при торможении в атмосфере. Но если существуют особые — стационарные — орбиты, на которых он не подчиняется законам электродинамики и потому не излучает, то должны существовать также дополнительные условия, которые выделяют эти орбиты из набора всех возможных.

Как появляются эти условия, легче всего показать, продолжив нашу аналогию со спутником.

У кругового движения, кроме радиуса орбиты r и скорости v движения по ней, есть еще одна характеристика — момент количества движения l, или, коротко, орбитальный момент l. Он равен произведению массы m на скорость v и на радиус орбиты r, то есть l = m v r, и для спутника может принимать произвольные значения в зависимости от величины r и v.

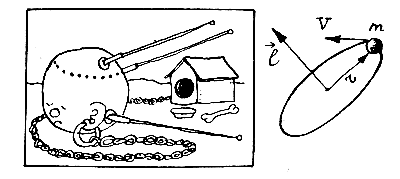
Условие стационарных орбит

Бор утверждал: электрон в атоме отличается от спутника тем, что его орбитальный момент l не может быть произвольным. — он равен целому кратному от величины ħ = h/2π (это обозначение предложил один из создателей квантовой механики, Поль Дирак)

mvr = n ħ.

Это и есть то дополнительное условие Бора, которое выделяет стационарные орбиты (единственно допустимые в атоме) из бесконечного числа мыслимых. А поскольку при таком выделении основную роль играет квант действия h, то и весь процесс назвали квантованием.

Из предыдущих двух условий Бор легко получил значения энергии Е_n радиусов r_n стационарных орбит:

r_n = (ħ²)/(m e²) • n²; Е_n = [-(m e⁴)/(2 ħ²)] • (1/n²).

Стационарные орбиты (а следовательно, и уровни энергии) нумеруются целыми числами n или k, которые пробегают бесконечный ряд значений: 1, 2, 3... При переходе с уровня n на уровень k электрон излучает энергию ΔЕ = Е_k — Е_n, а частота излучения, которое при этом возникает, определяется по формуле Эйнштейна;

ν = ΔЕ/h = (Е_k - Е_n)/(2πħ )

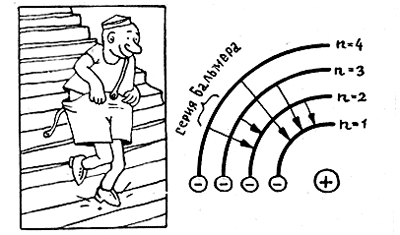
Если мы наблюдаем излучение, которое возникает при переходах электрона со всевозможных уровней k на какой-то определенный уровень п, то мы увидим не просто набор спектральных линий, а серию. Например, если n = 2, а k = 3, 4, 5, 6... то мы увидим серию Бальмера. Отсюда сразу же следует знаменитая формула Бора для частоты излучения атома водорода:

ν = [(me⁴)/(4πħ³)] • (1/n²-1/k²).

Что из нее следует?

Прежде всего она очень напоминает формулу Ридберга для атома водорода, которую тот нашел эмпирически задолго до Бора и о которой мы подробно рассказали в предыдущей главе. Если формула Бора верна, то из нее можно вычислить постоянную Ридберга R.

R = (me⁴)/(4 πcħ³).

Вычислили. И действительно, ее значение совпало с тем, которое давно было известно из спектроскопических измерений.

Это был первый успех теории Бора, и он произвел впечатление чуда.

Но это еще не все. Из теории Бора следовало, что радиус атома водорода в основном (невозбужденном) состоянии (n=1) равен

r₁ = ħ²/me² = 0,53 • 10^-8см = 0,53 Ǻ

Это означает, что размеры атомов (≈ 10^-8см), вычисленные по его формуле, совпадали с предсказаниями кинетической теории материи.

И наконец, теория Бора объяснила: как свойства линейчатого спектра связаны с внутренним строением атома. Интуитивно эту связь чувствовали всегда. Но только Бору впервые удалось выразить ее математически. Оказалось, что искомую связь осуществляет постоянная Планка h.

Это было неожиданно. Действительно, квант действия h возник в теории теплового излучения и никаким очевидным образом не был связан ни с атомами, ни с лучами, которые эти атомы испускают. И тем не менее именно он позволил вычислить абсолютные размеры атома и предсказать частоту света, излучаемого им. Угадать эту связь Бору, как и многим до него, помогла глубокая вера в единство природы.

Постулаты Бора (как и всякие постулаты) нельзя обосновывать логически или вывести из более простых. Они остаются произвольными творениями человеческого разума до тех пор, пока опыт не подтвердит следствий, которые из них вытекают. Тогда на их основе развиваются теории, а наиболее удачные из теорий называют законами природы.

Мы ограничимся только этими тремя следствиями теории Бора — на самом деле их значительно больше, и все они демонстрируют непонятную силу непонятных постулатов.

Раздумья Бора

Конечно, Бор пришел к ним несколько другим путем, чем мы с вами сейчас: когда человек впервые поднимается на незнакомую вершину, трудно ожидать, что он идет самым коротким путем. Только взойдя на пик, он видит, как можно было покорить его проще.

ПОСЛЕ БОРА

Несмотря на необычность постулатов Бора, его теория нашла довольно быстрое признание и достаточно много талантливых и сильных последователей. Если бы потребовалось определить отношение к ней физиков в те годы, то, пожалуй, пришлось бы назвать чувство облегчения, чувство освобождения от того постоянного напряжения, в котором все они до сих пор находились, пытаясь удержать в памяти разрозненные факты и хоть как-то связать концы с концами. Теперь все атомные явления, естественно, группировались вокруг непонятной, но простой модели; часть из них блестяще ею объяснялась, а другая требовала дальнейшего развития модели.

В частности, теперь очень просто можно было объяснить опыт Кирхгофа и Бунзена с парами натрия.

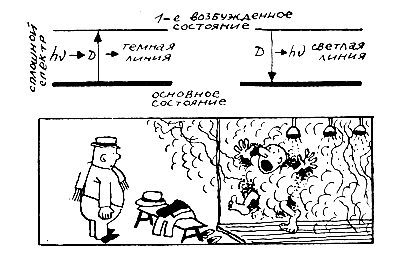
Действительно, пока луч от раскаленного тела не прошел через пары натрия, атомы которого находятся в основном состоянии, он содержит все длины волн. Проходя через пары, луч переводит атом натрия из основного состояния в первое возбуждение. На это затрачивается энергия кванта E = hν, частота которого ν как раз и совпадает с частотой линии D натрия. Поэтому прошедший свет уже не содержит лучей с этой частотой, и на шкале спектрографа мы видим сплошной спектр, перерезанный в желтой части темной линией D.

В обратном процессе, когда атомы натрия переходят из возбужденного состояния в основное, они излучают свет с той же частотой ν, которую прежде поглотили, то есть ту же линию D, но теперь уже ярко-желтую.

Несмотря на все успехи теории Бора, физики вначале принимали ее скорее как удобную модель, но не очень верили в реальность такой энергетической лестницы в атоме. Это сомнение разрешили Джеймс Франк (1882—1964) и Густав Герц (род. 1887) (племянник знаменитого Генриха Герца) в том же 1913 году. Как и всякая ясная идея, теория Бора не только объясняла старые факты, но также подсказывала пути для своей проверки.

Арнольд фон Зоммерфельд (1868—1951) — замечательный физик и блестящий педагог — был одним из первых в Европе, кто сразу же не только поверил в постулаты Бора, но и развил их дальше, «...следуя, как когда-то Кеплер при изучении планетной системы, внутреннему чувству гармонии». Он рассуждал так: если атом подобен солнечной системе, то электрон в такой системе может вращаться не только по окружности, как в модели Бора, но и по эллипсам, причем ядро должно находиться в одном из фокусов этих эллипсов.

Зоммерфельд

Эллипсы с одинаковой большой полуосью принадлежат одному и тому же значению главного квантового числа n, так как энергии электрона на таких орбитах равны между собой (Зоммерфельд знал доказательство, а нам придется поверить в это). Однако эллипсы различаются по степени сплющенности, которая зависит от орбитального момента. Вполне в духе идей Бора Зоммерфельд предположил, что при заданном n эллипсы могут быть сплющены не произвольным образом, а только так, чтобы орбитальное квантовое число l (которое их различает) принимало целые значения l = 0,1,2,... n - 1, то есть число допустимых эллипсов не превышает числа n — номер стационарного состояния.

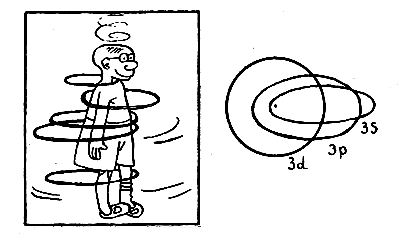
Орбитали

Бор и Зоммерфельд показали даже нечто большее: если учесть теорию относительности Эйнштейна, то окажется, что энергия электрона различна на всех эллипсах, а потому уровни энергии в атоме необходимо нумеровать двумя квантовыми числами: n и l. По той же причине спектральные линии, возникающие при переходах электрона между уровнями, с разными n, должны иметь тонкую структуру, то есть расщепляться на несколько компонент. По просьбе Зоммерфельда Фридрих Пашен проверил и подтвердил это следствие теории на примере линии гелия λ = 4686 Ǻ, которая соответствует переходу с уровня n = 4 на уровень n = 3 (с четвертого уровня на третий). Внимательно рассмотрев фотографию спектра гелия, он обнаружил, что линия в действительности состоит из тринадцати тесно расположенных линий.

Гелий

Это было удивительное совпадение, и в то время (1916 году) его сравнивали с вычислениями Леверье и Адамса, которые предсказали планету Нептун.

Но даже два квантовых числа — n и l не объяснили всех особенностей спектров. Например, если поместить излучающий атом в магнитное поле, то спектральные линии расщепляются совсем по-другому.

Расщепление спектральных линий в магнитном поле пытался обнаружить Фарадей еще в 1862 году в своей последней (уже неопубликованной) работе. Однако магнит, который он для этой цели использовал, был слишком слаб, и лишь в 1896 году Питер Зееман наблюдал явление, которое в свое время тщетно искал Фарадей.

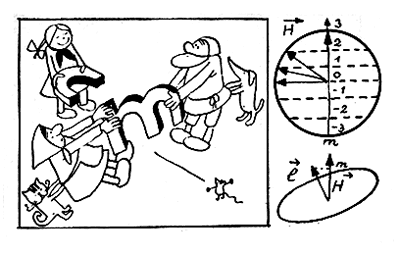
После работ Бора и Зоммерфельда явление расщепления спектральных линий в магнитном поле стали толковать следующим образом. Представьте, что перед вами электромотор. Даже не вникая в технические детали его устройства, вы со школьных лет знаете, что его ротор начнет вращаться, если через его обмотку пропустить электрический ток. Электрон, движущийся в атоме по замкнутой орбите, подобен витку тока в обмотке электромотора. И точно так же, как этот виток, орбита электрона в магнитном поле начнет поворачиваться. Однако в отличие от витка она не может занимать в атоме произвольные положения, поскольку этому препятствуют квантовые законы. Суть этих квантовых законов проще всего понять, взглянув на прилагаемый рисунок. На рисунке магнитное поле направлено снизу вверх, а орбита электрона изображена «с ребра», причем радиус орбиты численно равен значению орбитального момента l (на рисунке l = 3). Оказывается, законы квантования допускают только такие положения плоскости орбиты относительно магнитного поля Я, при которых проекция диаметра орбиты на направление поля H равна целому числу. Это третье магнитное квантовое число m, как легко видеть, принимает значения m = l, l — 1,..., 1, 0, — 1,..., — (l—1), — l, то есть всего (2l+ 1) значений.

Таким образом, в магнитном поле каждый уровень E_nl с заданными значениями квантовых чисел n и l расщепится еще на (2l+ 1) подуровня, E_nlm, каждый из которых однозначно определяется заданием трех целых квантовых чисел: n, l, m. А это, мы знаем, приводит к дополнительному расщеплению спектральных линий.

Усложняясь, теория Бора постепенно теряла свое первоначальное изящество и наглядность. На ее место пришла формальная модель атома, от которой требовалось лишь одно: дать правильную систематику термов. Термин «квантование» постепенно потерял свой прежний смысл: им обозначали теперь формальный процесс сопоставления целых (квантовых) чисел n, l и m каждому уровню энергии в атоме, а точнее, тому типу движения, в котором находится электрон. Квантовые числа n, l и m определяют стационарные орбиты в изолированном атоме. Внешние поля (электрическое и магнитное) влияют на движение электрона в атоме (расщепление уровней энергии), а это сразу же сказывается на структуре светового сигнала, который испускает атом (расщепление спектральных линий).

ФОРМАЛЬНАЯ МОДЕЛЬ АТОМА

Популяризация (как и всякая наука) имеет свои границы. Как правило, они определяются тем, что с некоторого момента становится невозможным использовать понятия и образы повседневной жизни. Для того чтобы эту границу преодолеть, нужно перейти на язык формальных понятий науки (для начала хотя бы примитивный). При всех попытках уйти от этого шага неизбежно возникает неосознанное глухое недовольство, а самая суть науки остается скрытой. Наоборот, преодолев минимальные затруднения, вы можете почувствовать силу логических построений науки и оценить красоту их следствий. Как правило, возникающие технические затруднения ничуть не больше тех, с которыми сталкивается любой школьник при изучении химии: довольно быстро он убеждается, что проще (а главное — понятнее) написать формулу Н₂О, чем каждый раз говорить: «Молекула, которая состоит из двух атомов водорода и одного атома кислорода».

Молекулы

Нечто похожее на химические формулы принято и в теории спектров, где главное квантовое число п обозначают цифрами: 1, 2, 3,... а орбитальный момент l — буквами, причем ряду чисел О, 1, 2, 3,... соответствует ряд букв s, р, d, f, ... Поэтому символ 3s, например, соответствует уровню энергии с квантовыми числами n = 3, l = 0, а символ Зр — уровню с n = 3, l = 1.

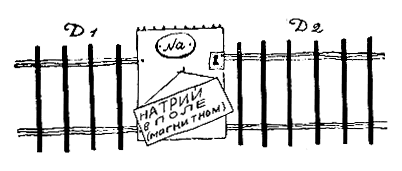
Натрий

В невозбужденном атоме натрия излучающий электрон находится в состоянии 3s. А темная линия D возникает в том случае, если при возбуждении атома электрон переходит в состояние Зр. При обратном переходе Зр -> 3s он излучает энергию и возникает ярко-желтая линия D.

А что произойдет, если излучающий натрий поместить в магнитное поле? Вначале, следуя Зоммерфельду, предполагали, что при этом верхний уровень Зр должен расщепиться на 3 компоненты 2l + 1 = 2•1 + 1 = 3, а нижний останется без изменения. В итоге каждая из линий D₁ и D₂ должна расщепиться на 3 компоненты.

Опыт противоречит такому заключению. Из рисунка видно, что линия D₁ расщепляется на 4 компоненты, а линия D₂ — на 6. Это явление — частный случай так называемого аномального эффекта Зеемана. Чтобы понять его причину, необходимо немного возвратиться назад и уяснить себе вопрос, которого мы раньше сознательно избегали: почему даже в отсутствие магнитного поля D-линия натрия состоит из двух тесно расположенных компонент D₁ и D₂?

Мучительно размышляя над этим вопросом, ученик Зоммерфельда Вольфганг Паули (1900—1958) пришел в 1924 году к открытию спина электрона (от английского слова spin — веретено). Он рассуждал примерно так: обе линии D₁ и D₂ соответствуют одному и тому же переходу с уровня n = 3, l = 1 на уровень n = 3, l = 0. Но их все-таки две! Значит, существует не один, а два верхних уровня Зр и еще какое-то дополнительное квантовое число, которое их различает: Свойство, которому соответствует это четвертое квантовое число S, он назвал «неклассической двузначностью электрона» и предположил, что оно может принимать только два значения: +¹/₂ и —¹/₂. Паули считал, что наглядное представление этого свойства невозможно.

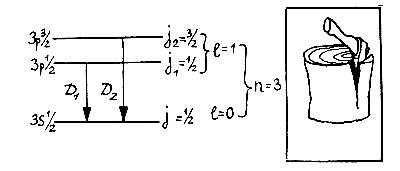
Открытие спина

Но уже в следующем году Джордж Уленбек (род. 1900) и Сэмюэл Гаудсмит (род. 1902) нашли наглядную модель для объяснения этого свойства электрона, допустив, что он вращается вокруг своей оси. Такая модель прямо следовала из аналогии между атомом и солнечной системой: ведь Земля вращается не только по эллипсу вокруг Солнца, но еще и вокруг своей оси (эту аналогию отмечал и Комптон в 1921, а Крониг — в 1923 году, но Паули резко против нее восстал).

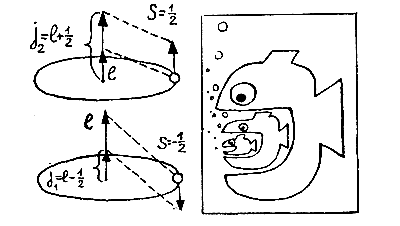
Свойство электрона

Уленбек и Гаудсмит предположили, что, кроме орбитального момента l, значения которого — целые числа и который возникает при движении по эллипсу, электрону присущ внутренний момент вращения, или спин S, равный по величине S = ¹/₂. Складываясь с орбитальным моментом l, этот внутренний момент S может его увеличить или уменьшить. В результате возникает полный момент j, равный либо j₁ = l — ¹/₂, либо j₂ = l + ¹/₂, в зависимости от взаимной ориентации векторов l и S. Если же l = 0, то полный момент и спин совпадают (j = S = ¹/₂).

Теперь все встало на свои места: уровень 3s в атоме натрия останется без изменения, так как соответствует моменту l = 0, но уровень Зр расщепится на два: 3 р _¹/2 и 3 p_³/2 энергии которых немного различны.

В магнитном поле каждый из уровней с полным моментом j (как и в случае момента l) расщепляется еще на (2j + 1) компонент, которые различаются значением магнитного квантового числа m. Таким образом, каждый из уровней 3s_1/2 и 3p_1/2 расщепится еще на два подуровня, а уровень Зр_3/2 — на четыре. В результате возникает та схема уровней и переходов между ними, которая изображена на рисунке (стр. 94) и которая полностью объясняет структуру линий.

Из рисунка видно, как усложнялась первоначальная модель Бора, в которой существовал только один уровень с n = 3. Когда приняли во внимание теорию относительности, он расщепился на два —Зр (n = 3, l=1) и 3s (n = 3, l = 0). С учетом спина электрона уровень Зр расщепляется еще на два подуровня — Зр_1/2(n = 3, l = 1, j = 1/2) и 3p _3/2(n = 3, l = 1, j = 3/2). И наконец, в магнитном поле мы получим систему уровней, изображенную на нашем рисунке, которая приводит к картине спектральных линий, наблюдаемых на опыте.

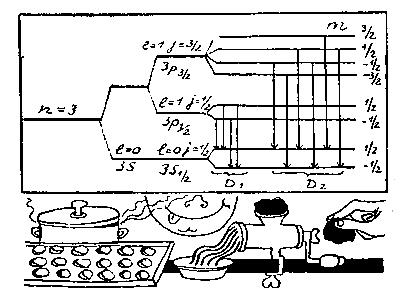
Модель Бора

Гипотеза о спине электрона — одна из самых глубоких в физике. Вполне осмыслить ее значение, не удалось до сих пор. И Паули был, конечно, прав, предостерегая от прямолинейных попыток представлять электрон как вращающийся волчок.

Влияние спина на физические процессы в атоме и на его строение проявляется иногда самым неожиданным образом. Одна из таких особенностей спина составляет содержание знаменитого принципа запрета Паули: в атоме не может быть двух электронов, квантовые числа которых n, I, m, S одинаковы. В дальнейшем мы видим, что только этот принцип позволил найти рациональное объяснение периодической системы элементов Дмитрия Ивановича Менделеева.

Даже по стилю изложения вы, наверное, сейчас заметили, насколько формальная модель атома беднее образами по сравнению с моделью Бора, насколько труднее рассказать о ней привычными словами и представить наглядно. И тем не менее вы, вероятно, ощутили ее силу: на ее основе можно объяснить и предсказать самые тонкие особенности спектров. Устрашающее количество спектральных линий удалось привести в порядок. Теперь, чтобы однозначно определить любую линию в спектре атома, достаточно было задать восемь квантовых чисел: четыре для исходного уровня излучающего электрона (n_i, l_i, m_i, S_i) и четыре для конечного (n_k, l_k, m_k, S_k).

К 1925 году эта героическая работа была закончена. Иероглифы были расшифрованы, что позволило нарисовать первую и пока грубую картину внутреннего строения атома.

Конечно, расшифровать спектр какого-либо элемента — задача даже сегодня не особенно легкая, и вполне квалифицированно сделать это могут только специалисты. В конце концов научиться читать даже расшифрованные иероглифы не так уж просто, и к тому же не обязательно уметь это делать всем. Но поскольку ключ к шифру известен, то научиться с ним работать может любой.

И теперь уж никого не угнетают длинные таблицы спектральных линий, как не пугают зоологов миллионы видов растений и животных: после трудов Линнея, Ламарка и Дарвина все они подчинены строгой систематике.

Со спектральными линиями произошло то же самое, что и с настоящими египетскими иероглифами: пока их не прочли, они были интересны только египтологам, остальные интересовались ими лишь абстрактно. Но когда иероглифы и спектры расшифровали, одним удалось прочесть историю целого народа, другим — узнать устройство атома. А это уже интересно всем.

Несмотря на успехи формальной модели атома, она уже не удовлетворяла тому критерию логической простоты, которая производит впечатление очевидности (и которая так выгодно отличала модель Бора). Постепенно она стала настолько сложной, что вызвала недоверие к себе и некоторое чувство усталости, очень похожее на то, какое владело физиками до схемы Бора. К тому же все попытки распространить модель Бора на более сложные атомы кончались неудачей. В состоянии некой растерянности физики стали подвергать сомнению все: справедливость закона Кулона, применимость электродинамики и механики в атомных системах и даже закон сохранения энергии. Все примерно понимали, что кризис этот возник от столкновения эмпирических данных, принципов теории квантов и остатков классических представлений, отказаться от которых пока было нельзя, поскольку взамен их не было предложено ничего определенного.

При изучении квантовых явлений исследователи пользовались по-прежнему классическими понятиями. Но у атомных объектов не было свойств, которые бы этим понятиям соответствовали, и потому природе задавали, в сущности, незаконные вопросы. Или, точнее, вопросы на языке, которого она не понимала. Тогда начались поиски общего принципа, из которого бы логически следовали и формальная модель атома, и другие особенности атомных объектов. «Пусть вначале этот единый принцип будет непонятным, но пусть он будет один» — таково было общее желание.

В ответ на это стремление в том же 1925 году возникла квантовая механика — наука о движении электронов в атоме. Ее создало новое поколение физиков. По игре случая все они родились почти одновременно: Вернер Гейзенберг — в 1901, Поль Адриен Морис Дирак — в 1902, Вольфганг Паули — в 1900 году. Лишь немного старше их были Луи де Бройль и Эрвин Шредингер. Им выпало счастье записать образы и понятия атомной механики на языке формул. Как им это удалось — мы узнаем немного позже.

НИЛЬС ХЕНРИК ДЭВИД БОР (1885—1962)

По рисункам можно проследить эволюцию понятия «атом» от Демокрита до Бора. Эго очень поучительная история, которая всегда вызывает не только чувство уважения к известным и безвестным ученым, но главным образом — чувство удивления, что такое познание вообще оказалось возможным, причем в такой совершенной и гармоничной форме.

Как и всякое истинно великое открытие, открытие Бора трудно сделать, но легко понять. Сила идей Бора в их недоказуемой простоте и доступности. В главной своей сути они понятны любому грамотному человеку. Бор дал образ, который позволял ориентироваться среди необычных понятий квантовой механики, образ, который стал символом нашего века. Если учесть к тому же, что при всей своей простоте образ этот верно отражает основные свойства атомов, то сразу станет ясна его исключительность.

Идеи Бора

Из ста физиков, взятых наугад, сегодня, пожалуй, только один или два читали знаменитые статьи Бора, напечатанные в 1913 году. Однако любой из них подробно объяснит идеи, которые в них изложены. А это означает, что сейчас идеи Бора уже не предмет науки, а необходимый элемент культуры — самое высшее, чего может достичь любая теория.

На склоне лет Нильс Бор приехал в нашу страну и посетил Грузию. В один из дней в долине Алазани он отдыхал с группой грузинских физиков. Неподалеку от них расположились крестьяне и по старинному обычаю во главе с тамадой пели песни и пили вино. Нильс Бор — человек не только великий, но и любознательный подошел к ним и был принят с традиционным радушием. «Это знаменитый ученый Нильс Бор...» — начали объяснять физики. Но тамада жестом остановил их и, обращаясь к сотрапезникам, произнес тост: «Друзья! К нам в гости приехал самый большой ученый мира профессор Нильс Бор. Он создал современную атомную физику. Его труды изучают школьники всех стран. Он приехал к нам из Дании, пожелаем же ему и его спутникам долгих лет жизни, счастья, крепкого здоровья. Пожелаем его стране мира и благополучия». Речь тамады тихо переводили Бору, и когда он кончил говорить, с земли поднялся старик, взял обеими руками руку Бора и бережно ее поцеловал. Следом за ним поднялся другой горец, наполнил рог вином и, поклонившись Бору, осушил рог.

Нильс Бор всю жизнь провел среди парадоксов квантовой механики, но даже его поразила реальность происходящего: он заплакал от удивления и благодарности.

ВОКРУГ КВАНТА

ОПЫТНОЕ ДОКАЗАТЕЛЬСТВО ПОСТУЛАТОВ БОРА

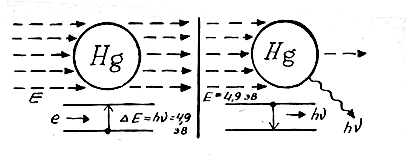
Опыт Франка и Герца, по существу, очень похож на опыт Кирхгофа и Бунзена, только атомы натрия в нем они заменили атомами ртути, а вместо луча направили на них пучок электронов, энергию которых они могли менять. При этом Франк и Герц наблюдали интересное явление: пока энергия электронов была произвольной — число электронов, прошедших через атомы ртути, было равно числу электронов исходного пучка. Когда же энергия их достигала определенной величины (в опытах она равнялась 4,9 электрон-вольта, или 7,84 • 10^-12 эрг), число электронов, прошедших ртуть, резко падало — они поглощались атомами ртути. Одновременно с этим в спектре паров ртути вспыхивала яркая фиолетовая линия с длиной волны λ = 2536Ǻ, то есть с частотой ν = 1,18 • 10¹⁵ сек^-1. Энергию кванта с такой частотой легко вычислить — она равна E = hν = 6,62 • 10^-27 • 1,2 • 10¹⁵ = 7,82 • 10^-12 эрг, то есть почти точно равна затраченной энергии электрона. Очевидно, это излучение возникает при обратном переходе атома ртути из возбужденного состояния в основное.

Легко видеть, что наблюдаемая картина — прямое опытное доказательство обоих постулатов Бора: в атоме реально существуют стационарные состояния, и поэтому он не способен поглощать произвольные порции энергии. Переходы электрона между уровнями в атоме возможны только скачками, а частота излучаемых квантов определяется разностью энергии уровней и вычисляется по формуле Эйнштейна ΔЕ = hν. Конечно, «легко видеть» это только сейчас, а в 1913 году даже сами Франк и Герц объяснили свой опыт совсем по-другому.

Ртуть

«КВАНТОВАНИЕ» СОЛНЕЧНОЙ СИСТЕМЫ

Мы много раз сравнивали атом с солнечной системой, хотя и не придавали глубокого смысла этой аналогии. Тем более неожиданно, что солнечная система, как и атом, тоже подчиняется некоему «правилу квантования». Это правило не имеет ничего общего с квантовой механикой, но тем не менее любопытно, что расстояния планет от Солнца (как и радиусы орбит в атоме) меняются не беспорядочно, а подчиняются довольно строгому закону.

Факт этот был известен Иоганну Кеплеру, и еще в молодости, много размышляя о «гармонии сфер», он пришел к выводу, что в промежутках между сферами, построенными на орбитах планет, можно вписать пять правильных многогранников.

Профессор Даниэль Тициус в 1772 году выпустил в Бонне книгу «Созерцание природы», в которой привел табличку расстояний от Солнца до планет в условных единицах (расстояние до ближайшей к Солнцу планеты Меркурий принято за 4).

Меркурий ... 4 = 4;

Венера...... 7 = 4 + 1 • 3;

Земля....... 10 = 4 + 2 • 3;

Марс........ 16 = 4 + 4 • 3;

Юпитер...... 52 = 4 + 16 • 3;

Сатурн...... 100 = 4 + 32 • 3.

Позднее прибавился

Уран....... 196 = 4 + 64-3.

Впоследствии Боде уточнил закон Тициуса, приняв расстояние до Меркурия за 8 условных единиц и записав общую формулу для планетных расстояний в виде: R = 8 + 3 • 2ⁿ,

где п = 0, 1, 2, 3, 4, 6, 7, 8.

Замечательно, что в приведенной схеме нет планеты с номером n = 5, которая должна была бы помещаться между Марсом и Юпитером. Но как раз в этом месте расположен пояс астероидов — малых планет. По мнению астрономов, это осколки некогда существовавшей большой планеты Фаэтон.

Закон Тициуса и Боде еще до конца не понят, хотя существует несколько его доказательств (одно из них принадлежит советскому ученому Отто Юльевичу Шмидту). По-видимому, полное объяснение закону будет найдено вместе с разгадкой происхождения нашей солнечной системы.