Земля и яблоко

Классической механике подвластны разнообразнейшие силы. Тянут железо магниты, отталкиваются от дороги колеса автомобиля, ударяются, расходясь в стороны, бильярдные шары - все это неукоснительно подчиняется законам Ньютона.

Но раз уж мы в этой книжке размышляем о падающих телах, побеседуем поподробнее об одной только силе тяготения.

Я уже много говорил о ней, вездесущей и таинственной, вместе с вами доискался ее главной особенности - неизменной пропорциональности тяжелой масса тела, недоумевал по поводу ее странного "действия без прикосновения". Эта поразительная ее особенность остается для нас загадкой, которую на этих страницах еще рано пытаться разгадывать. Но хоть мы не в состоянии объяснить, почему сила тяжести проникает через пустоту, нам пора задуматься над тем, как это происходит.

Сегодня всем известно: вдали от Земли тяжести нет. Это ясно каждому шестикласснику, это вошло в сознание из бесчисленных книжек, газетных статей, радиопередач. Во времена же Ньютона мир выглядел иным. О том, что сила тяжести не везде одинакова, лучшие умы могли только догадываться. Никаких опытов, свидетельствующих о ее уменьшении с высотой, не было. Наоборот, на башне и в подвале тяжелое ядро представлялось одинаково тяжелым.

И все-таки Ньютон, приглядевшись к перемещениям небесных тел, уверенно заявил: с увеличением расстояния от Земли тяготение убывает.

А как убывает? Быть может, на высоте облаков уже нет тяготения? Если верить упорной легенде, Ньютон ответил на это "как", созерцая в своем саду падающее яблоко. На самом деле, если и существовало это историческое яблоко, то, разумеется, не оно одно навело великого физика на его открытие. Были и другие, куда более существенные подсказки: замечательные идеи и вычисления Галилея, прозорливые слова Кеплера и математические закономерности, подмеченные им в движении планет, нескончаемые размышления самого Ньютона об инерции, массе, падении тел.

Земля и яблоко

Догадка эта даже сегодня не может представиться легкой и естественной. Если она и проста, то наверняка гениальна. Сила тяготения F пропорциональна массам притягивающихся тел m₁ и m₂, но она убывает тем сильнее, чем больше становится квадрат расстояния между центрами притягивающихся масс r². Именно квадрат! Не просто расстояние, не куб его, а квадрат. И именно между центрами масс. Дело происходит так, как если бы вся масса каждого тела было сосредоточена в бесконечно малом объеме - в точке, совпадающей с центром тяжести. Понять и обосновать это Ньютону стоило больших трудов.

Такова сущность замечательного ньютоновского открытия, которое вскоре стало знаменитым и получило название закона всемирного тяготения. Вот формула:

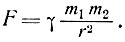
Символ γ означает "постоянную тяготения" - множитель пропорциональности, Уравновешивающий обе части равенства. Физический его смысл прост - это сила притяжения двух тел массой по грамму, находящихся в сантиметре друг от друга. γ можно узнать из эксперимента: измерить эту силу, заставив притягиваться два шарика с массой по грамму, подвешенных рядом на тонких нитях в сантиметре друг от друга. В таком грубом опыте, правда, никакого измерения не получится - граммовые шарики притягиваются ничтожно слабо. Успех здесь принесен другим, более тонким опытом, выполненным английским физиком Кавендишем.

Закон всемирного тяготения