Упражнения на эскалаторе

На Земле Клио был водворен в камеру и наказан за побег принудительным уроком физики. Тема урока - релятивистские законы сложения скоростей.

И вот учебный каземат. Властным взглядом майор Прошкин усадил заключенного Клио за парту. Написал на доске:

"Задача. Эскалатор в метро ползет вниз со скоростью три километра в час. Пассажиру некогда, и он сбегает по эскалатору со скоростью три километра в час относительно ступенек. Какова скорость пассажира относительно стен шахты?"

- Прошу решить, - сухо приказал майор.

Клио вспомнил, как давно-давно, еще маленьким шалопаем, школяром-третьеклассником, он получил похожую задачу. Тогда он написал 3 + 3 = 6 и заработал пять с плюсом. И сейчас взрослый Клио решил задачу так. Робко написал на доске результат сложения скоростей пассажира и эскалатора: 6 километров в час.

Майор сказал, что ответ правильный, но строго добавил:

- Однако, когда вы, задумав убежать в прошлое, захотели так же просто сложить скорости, близкие к световой, задача не решилась.

- Почему же? - спросил недоумевающий Клио.

- Потому, что при малых относительных скоростях ничтожны поправки, вносимые теорией Эйнштейна. А при скоростях, близких к световой, они огромны. Их необходимо учитывать, чего вы не сделали.

Клио сокрушенно молчал.

- Скажите, что такое скорость? - терпеливо спросил майор.

- Путь, пройденный за какое-то время, - с готовностью ответил Клио.

Прошкин согласился:

- Да. Но вот что надо помнить. Когда вы беззаботно складывали скорости по правилам школьной арифметики, то молчаливо допускали, что масштабы пути и времени для шахты, для пассажира и для эскалатора одинаковы. Может это быть, если скорость эскалатора и пассажира близки к скорости света? Может?

Я вас спрашиваю!..

- Наверное, нет, - неуверенно промямлил заключенный.

- Не "наверное", а наверняка нет! - воскликнул Прошкин. - Как только эскалатор помчался относительно шахты почти со скоростью света и пассажир побежал с подобной скоростью относительно эскалатора (допустим такое ради сохранения прежнего примера), у каждого участника этого сложного движения появляются релятивистские оценки событий в других системах отсчета. Для шахты метры эскалатора будут укоротившимися, секунды - удлинившимися, для эскалатора I метры пассажира сократятся и секунды пассажира станут дольше. Поэтому для шахты скорость пассажира будет хоть и больше скорости эскалатора, но меньше световой. Так что и этим воровским способом обогнать свет и, значит, удрать во вчерашний день не удастся. Вот она, ваша ошибка, гражданин Клио! Поражаюсь вашему невежеству!

Клио опустил голову. Он был посрамлен. Ему было мучительно стыдно. А майор продолжал:

- Далее допустите совсем уж невероятное происшествие - в метро погас свет. Бегущий пассажир вынимает из кармана фонарик и освещает себе дорогу. Свет из фонарика мчится со скоростью света. Это - относительно фонарика. А относительно шахты?

- Э... Вдвое больше, гражданин майор...

- Неверно! Ничего вы не поняли! Относительно шахты скорость света - та же. Она не увеличивается ни на йоту! Ведь мы с вами вернулись в своих рассуждениях туда, откуда отправлялись, - ко второму постулату Эйнштейна: скорость света не зависит от движения источника. Под конец урока майор подошел к доске.

- Если бы вы, гражданин Клио, проштудировали

графики Минковского (в этой книжке - "необязательные" главы двенадцатая и тринадцатая), то вряд ли затеяли бы эту свою нелепую попытку убежать в прошлое. Мировая линия вашей пиратской "Медузы" ни при каких условиях не может пересечь световую линию.

В той мировой точке, где "Медуза", сорвавшись с крыши мчащегося звездолета, полетела вперед, ее мировая линия лишь чуточку круче наклонилась к световой линии, попав в область скоростей, где для Земли еще дольше секунды и короче километры. Вот график (калибровочных линий времени и расстояний я не рисую):

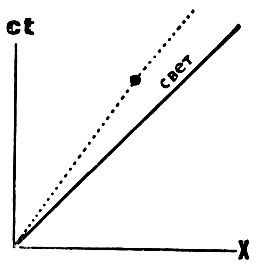
Мировая линия "Медузы" лишь чуть нагнулась, и скорости сложились совсем не арифметически. Вот формула: суммарная скорость

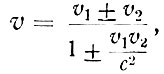
где v₁ - скорость первой движущейся системы отсчета, в которой движется со скоростью v₂ вторая система отсчета; знак плюс - для совпадающих по направлению движений, минус - для противоположных. Когда скорости v₁ и v₂ малы по сравнению со световой, выходит обычное классическое v = v₁ ± v₂. Ясно?

- Ясно, - не очень уверенно сказал Клио.

Ну, а читателям, я надеюсь, вполне ясно.