"Размышления о движущей силе огня..."

Роль Клапейрона в создании термодинамики в большинстве работ по истории естествознания представляется скромной. Общепринятым считается мнение, что в области термодинамики им только установлен вид уравнения состояния идеального газа и получено уравнение фазового перехода, обобщенное впоследствии Клаузиусом. Обычно его имя упоминается в связи с исследованиями Карно, причем единодушно утверждается, что в своей работе Клапейрон лишь пересказал идеи Карно, графически проиллюстрировав их. Однако такое отношение к научному творчеству французского ученого не соответствует действительности. Результаты, полученные Клапейроном в области термодинамики, далеко не ординарны. Его вклад в эту область знаний весьма существен. Установленное им уравнение играет очень важную роль в различных термодинамических расчетах. Эти уравнения можно поставить в один ряд с законами Кеплера в небесной механике или с законом Ома в электричестве.

Широко распространенное мнение о второстепенной роли Клапейрона в развитии термодинамики сложилось под влиянием ряда случайных факторов. Прежде всего следует отметить, что еще в начале "Размышлений..." сам Клапейрон предупреждает читателей, что цель данной работы - развитие идей Карно. Неоднократно ссылаясь в своих рассуждениях на работу Карно, он не проводит четкой границы между собственными результатами и результатами, к которым пришел его предшественник. Более того, название работы Клапейрона почти совпало с названием работы Карно. С учетом этого понятно, почему европейские физики, которые знакомились с идеями Карно не по публикациям автора, а по работе Клапейрона, имели некоторые основания утверждать, что "Размышления..." Клапейрона всего лишь добросовестное переложение идей своего соотечественника. К этому иногда снисходительно добавляют, что Клапейрон пересказал идеи Карно, математически и графически обработав их. В последующем изложении попытаемся непредвзято подойти к оценке научного творчества Клапейрона в области термодинамики и четко выделить все то новое, оригинальное, что содержится в его работе, посвященной исследованию тепловых процессов.

Как уже отмечалось, Клапейрон много лет с увлечением занимался подготовкой лекционного курса "Паровые машины". При очередной переработке этого курса он обратился к источникам соответствующей тематики, изданным в годы его работы в России. Вполне естественно, что в число этих источников попала и работа Карно¹. Детально ознакомившись с ее содержанием, Клапейрон сумел понять главную мысль автора. Идеи, высказанные Карно, увлекли его. Для того чтобы наглядно представить ход рассуждений автора, Клапейрон разработал графический метод изображения термодинамических процессов.

¹ (Имеется предположение, что Клапейрон был лично знаком с Карно)

Графический метод изображения процессов, осуществляющихся в газах, не только позволял наглядно представить характер изменения параметров, описывающих состояние исследуемого газа, но и давал возможность применить математические приемы для расчета эффективности того или иного процесса или цикла. Последний фактор особенно важен потому, что Клапейрон был великолепным математиком, свободно владеющим аппаратом дифференциального и интегрального исчислений.

Объем работы Клапейрона небольшой: в немецком издании В. Оствальда, в серии "Классики точного знания", она представлена на 38 страницах и состоит из восьми глав, каждая из которых может рассматриваться как вполне самостоятельное исследование.

В первой главе содержится материал, который вводит читателя в курс дела. Здесь же сформулирована проблема, которую собирается решить автор. Основное внимание Клапейрон обращает на значимость фактов, вытекающих из экспериментальных исследований свойств газов. Хотя для газов, пишет он, найдены законы Бойля-Мариотта и Гей-Люссака, связывающие его параметры в различных состояниях, и точность этих законов не вызывает сомнений у ученых, однако, продолжает автор, до сих пор ничего неизвестно о том количестве теплоты, которым обладает газ, находящийся в определенном состоянии, и которое освобождается из него при различных процессах. Кроме того, из этих законов невозможно получить количественное отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме.

Вполне понятно, что в первую очередь Клапейрона интересовали экспериментальные факты, посвященные исследованию тепловых свойств газа, так как именно знание этих свойств способствовало бы отысканию путей повышения эффективности действия паровых машин. Поиск этих путей и составлял главную цель инженеров и ученых того времени.

Прежде всего Клапейрон отмечает уязвимость исследований П. Лапласа и С. Пуассона по тепловым свойствам воздуха, так как в их рассуждениях совершенно бездоказательно принимается за основу положение, согласно которому при данной температуре отношение изобарной теплоемкости к изохорной одинаково для всех газов и значение этого отношения есть неизвестная функция температуры, вид которой и требуется установить.

Клапейрон правильно понял основную мысль рассуждений Карно. Из всего содержащегося в работе Карно он выделил, по его мнению, наиболее важное:

1. если газ при некотором значении давления и объема перейдет без изменения температуры в состояние с новыми значениями объема и давления, то полученное или отданное при этом количество теплоты не зависит от природы исследуемого газа;
2. различие между удельной теплоемкостью при постоянном давлении и удельной теплоемкостью при постоянном объеме одинаково для всех газов;
3. при изменении объема газа без изменения температуры количество теплоты, отданное или полученное этим газом, составит арифметическую прогрессию, если объем газа будет изменяться в геометрической прогрессии.

Клапейрон отмечает, что существует возможность математически подтвердить справедливость вышесказанного. "Этот новый аргументированный метод, - пишет он по этому поводу, - по моему мнению, заслуживает внимания математиков. Я полностью подтверждаю его безупречность и считаю, что, пользуясь этим методом, можно получить важные результаты". Далее Клапейрон продолжает обсуждение основных положений, содержащихся в работе Карно, отмечая при этом, что именно они будут исходными в его последующих рассуждениях.

Прежде чем излагать рассуждения Клапейрона, заметим, что он безоговорочно принял представления Карно о вещественной природе теплоты: как и Карно, Клапейрон в своей работе оперирует теплородом, считая, что при различных процессах в газах количество теплорода остается постоянным.

Как и у Карно, движущая сила, по Клапейрону, развивается в том случае, если теплород переходит от одного горячего тела к другому, холодному, количественно при этом не изменяясь. Правда, он, как и Карно, понимает слабое место в своих рассуждениях: вещественная теория теплоты не всегда соответствует теоретическим представлениям, развиваемым им. Термин "движущая сила" у Клапейрона, как и у Карно, соответствует механической энергии, или произведенной работе.

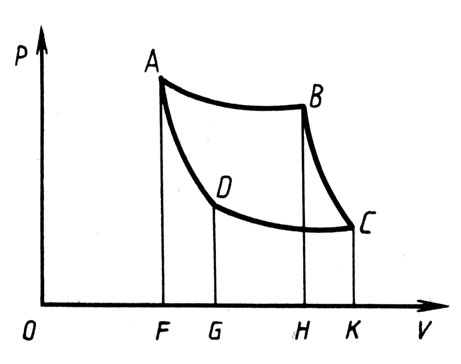
Рис. 6. В осях р-V изображается цикл, предложенный Карно

В самом начале второй главы Клапейрон излагает мнение Карно о том, что в паровой машине возможен не только прямой процесс - получение движущей силы за счет перехода теплорода от горячего тела к холодному, но и обратный - перенос теплоты от холодного тела к горячему за счет работы, произведенной внешними силами. Далее он выделяет наиболее существенный момент рассуждений Карно: максимальная работа совершается в том случае, когда передача теплоты от одного тела к другому совершается при одинаковой температуре этих тел. В этой же главе Клапейрон предлагает способ графического представления тепловых процессов, осуществляющихся в газах, и в осях р-V изображает цикл, предложенный Карно (рис. 6). Представим себе одно тело, температура которого Т поддерживается постоянной, пишет Клапейрон, и другое тело, температура которого t ниже, чем Т. Например, первое тело - стенки котла, который получает теплоту за счет сгорания топлива, расходуемую на образование пара, и второе - представляющее собой конденсатор обычной паровой машины, где поток холодной воды отбирает теплоту, которой обладает полученный при данной температуре пар. Чтобы упростить дальнейшие рассуждения, обозначим первое тело А, второе - В.

Возьмем какой-либо газ, температура которого Т, и приведем его в соприкосновение с телом А, имеющим ту же температуру. Состояние этого газа изобразим точкой, абсцисса которой OF соответствует объему исследуемого газа, а ордината - давлению. Если газ заключить в сосуд, объем которого может изменяться, и дать ему возможность расширяться в этом сосуде так, чтобы за счет излучения или теплопередачи теплота не расходовалась, то убыль теплорода при этом будет пополняться за счет тела А. Температуpa газа при расширении будет оставаться постоянной и равной Т. Давление газа в этом случае будет изменяться в соответствии с законом Бойля-Мариотта. Графически этот процесс может быть представлен в виде кривой АВ.

Предположим, что расширение газа будет продолжаться до тех пор, пока объем газа не станет равным ОН. Новому значению объема будет соответствовать давление ВН. В процессе расширения газ совершит работу, которая может быть вычислена как интеграл от произведения давления на изменение объема. Графически эта работа может быть представлена площадью фигуры, образованной осью абсцисс, ординатами OF и ВН и отрезком гиперболы АВ.

Удалим теперь тело А и, заключив газ в теплонепроницаемую оболочку, дадим ему возможность расширяться. Тогда часть теплорода перейдет в "скрытое" состояние, температура газа понизится и давление будет падать намного быстрее по неизвестному, как сообщает Клапейрон, закону, представленному графически линией ВС. (Интересно то, что уравнение, описывающее адиабатный процесс, было выведено французским физиком Пуассоном еще до того, как была издана работа Карно.)

Продолжим расширение газа до тех пор, пока за счет перехода теплорода в скрытое состояние температура газа не изменится от Т, соответствующей температуре тела А, до температуры t, равной температуре тела В. При этом объем газа станет равным ОК и соответствующее ему давление СK.

Из рисунка видно, что в течение второго этапа своего расширения газ совершает определенную работу, которая графически может быть представлена площадью неправильного четырехугольника ВСKН.

Теперь, когда газ достиг температуры t, равной температуре тела В, приведем его в контакт с этим телом. Исключая теплопроводность и излучение в окружающее пространство, будем сжимать исследуемый газ. Вследствие сжатия температура газа начнет повышаться, станет заметнее стремление теплорода перейти к телу В в таком количестве, чтобы температура газа продолжала оставаться равной t. В соответствии с законом Бойля-Мариотта давление газа будет возрастать. Графически это будет соответствовать ординатам гиперболы CD; абсцисса при этом будет обозначать объем газа.

Продолжим сжатие до тех пор, пока не добьемся того, что телу В будет передана теплота, в точности равная той, которая была сообщена газу телом А во время контакта с ним в первой фазе процесса расширения. Объем газа при этом станет равным OG и соответствующее ему давление GD. В этом состоянии газ обладает точно таким же количеством теплорода, как и в начале процесса, когда его объем был равен OF и давление AF, Если теперь тело В отнять и удалить, а сжимаемый газ заключить в теплонепроницаемую оболочку, то благодаря увеличению давления объем газа уменьшится от OG до OF, скрытый теплород при этом освобождается и температура газа будет постепенно повышаться. Давление в этом случае увеличивается и достигает значения, соответствующего ординате AF, если объем газа уменьшится до OF. Температура газа при этом достигнет начального значения, равного Т.

Далее Клапейрон ставит задачу вычисления работы, совершаемой газом в этом цикле. Ход его рассуждений предельно прост. Уменьшение объема от ОК до OF требует совершения внешними силами работы, значение которой может быть представлено неправильными четырехугольниками DC KG и ADGF. Вычитая площади фигур ABCKFA и ADCКFА, которые представляют числовые значения работы расширения и сжатия, найдем их разность, равную площади, ограниченной фигурой ABCD. Числовое значение площади этой фигуры в осях р-V равно работе, совершаемой газом за описанный цикл. При расчетах подразумевается, замечает Клапейрон, что конечное состояние в точности совпадает с начальным. Расход теплорода при этом отсутствует: та теплота, которую газ отбирает от тела А при расширении, передается телу В при сжатии во время контакта этих тел с рабочим телом. Клапейрон приходит к выводу, что "механическая энергия развивается благодаря переходу теплорода от теплого тела к холодному; этот переход совершается без того, чтобы где-нибудь имелся контакт между телами, имеющими разные температуры".

Заканчивая описание прямого цикла, Клапейрон рассматривает обратный, в результате которого развивается теплота за счет работы внешних сил. Здесь он отмечает, что если внешними силами произвести работу над газом, равную совершенной им в прямом процессе, то при этом произойдет перенос теплоты от тела В к телу А в таком же количестве, как перенесено в прямом процессе от тела А к телу В.

Продолжая изложение, Клапейрон распространяет свои выводы на двухфазную систему - жидкость и ее пар. Для этого случая цикл также может быть представлен графически (рис. 7). Участок с постоянным давлением соответствует фазовому переходу пар - жидкость при постоянной температуре. Указывая на возможность обратного цикла для двухфазной системы, Клапейрон приходит к выводу: "Количество работы, совершаемое газом, и количество теплоты, перешедшее от теплого тела к холодному, - величины одинакового типа, которые могут переходить друг в друга, взаимопревращаться. Здесь дело обстоит так же, как и в механике, где тело, которое может падать с определенной высоты, и тело, обладающее определенной скоростью, характеризуются величинами одного вида, которые могут благодаря определенным устройствам превращаться друг в друга".

Этот вывод он повторил вслед за Карно, дневниковые записи которого оставались еще неизвестными. Из приведенного отрывка ясно, что Клапейрон, вплотную подойдя к закону сохранения и превращения энергии, не сумел далее развить свои рассуждения, не смог обобщить их и сформулировать этот важнейший закон естествознания. Пройдет еще около 10 лет, прежде чем этот закон будет окончательно установлен и утвержден в физике Р. Майером, Дж. Джоулем, Г. Гельмгольцем и другими исследователями.

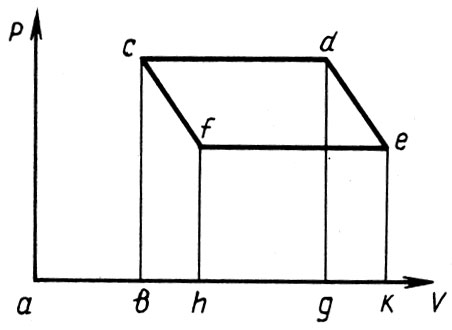
Рис. 7. Клапейрон распространяет свои выводы на двухфазную систему - жидкость и ее пар

В третьей главе Клапейрон приступает к математическим расчетам. В первую очередь он дает запись объединенного газового закона, который называет "уравнением состояния Гей-Люссака-Мариотта". В записи Клапейрона этот закон имеет вид:

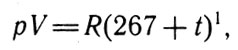
Объединенный газовый закон (1)

где

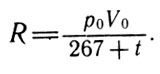
Расчёт R

Несмотря на то что уравнение (1) встречается и в работе Карно, оно справедливо названо уравнением Клапейрона. Именно Клапейрон при расчете различных процессов, осуществляющихся в газах, первым использовал его для тепловых расчетов, четко определив область его применения.

(В настоящее время более точные измерения дают для коэффициента объемного расширения газов не ¹/₂₆₇, а ¹/₂₇₃)

В дальнейшем для удобства математических расчетов Клапейрон принимает температуру горячего тела равной t; температура холодного тела при этом отличается на бесконечно малую величину At и равна t-Дt и предполагает бесконечно малые изменения параметров газа при совершении им элементарного цикла, составленного из двух изотермических и двух адиабатных процессов. В этом случае с достаточной точностью отрезки изотерм можно считать отрезками прямых; аналогично можно рассматривать и отрезки адиабат, замыкающих изотермы для температур t и t-At. Работа, совершаемая газом в течение цикла, графически представленная в осях "давление - объем", численно равна площади фигуры ABCD, которая представляет собой параллелограмм. Следовательно, работа, выполненная за описываемый цикл, может быть вычислена как произведение приращения давления (Ар) на приращение объема. Производя эти расчеты, Клапейрон получает выражение для работы, совершаемой газом при нагревании его на AΔt:

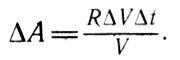
Выражение для работы

Теплота, переданная при этом газу, является функцией температуры, которая в свою очередь, как это следует из уравнения состояния, сама есть функция объема и давления. Путем математических операций Клапейрону удалось найти также выражение для теплоты (ΔQ) и записать выражение интересующего его отношения ^ΔA/_ΔQ.

Данное выражение, пишет Клапейрон, представляет собой наибольшее значение работы, которая может быть совершена газом при переходе единицы теплоты от тела с температурой t к телу с температурой t-Δt. Эта работа не зависит от рода вещества, которое используется при переносе теплоты, одинакова для всех газов и не зависит от количества вещества, участвующего в этом цикле. Однако ничего нельзя сказать, что это отношение не зависит от температуры. Вполне вероятно предположить, что отношение ^ΔA/_ΔQ представляет собой неизвестную функцию температуры (С=f(t)), одинаковую для всех газов и имеющую важное значение в теории тепловых машин.

Дальнейшие математические расчеты, выполненные Клапейроном, приводят к выражению

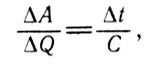
Функция Карно (2)

в котором встречается эта функция, названная позднее функцией Карно (С). Клапейрон справедливо утверждает, что функция Карно имеет большое значение в теории газов, и в последующих главах предпринимает многократные попытки рассчитать ее в широком диапазоне температур. Однако полученные результаты не удовлетворяли его. В этой же главе ученый приводит полученную им формулу

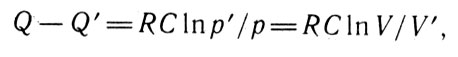
Изменение объема газа (3)

из которой следует, что при изменении объема гaза или его давления при постоянной температуре в одинаковое число раз газ отдает или принимает одно и то же количество теплоты, что совпадает с результатом, установленным Дюлонгом экспериментально.

Далее, используя эту формулу, Клапейрон математически поясняет, почему газ, расширяясь в пустоту, не нагревается и не охлаждается. По Клапейрону, понижение давления от р' до р или увеличение объема от V до V при постоянной температуре вызовет изменение количества теплоты, содержащееся в рабочем теле:

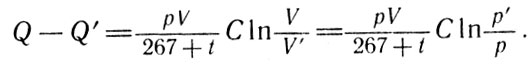
Количество температуры (4)

Числовое значение ^lnр'/_р очень большое, но произведение ^рlnр'/_р будет очень малым, если газ расширяется в разреженное пространство, так как р→0. Для этого случая Клапейрон находит выражение

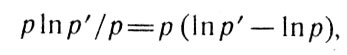
Теплота

т. е. теплота, развиваемая газом при его расширении в некоторый сосуд, будет тем меньше, чем ниже давление в этом сосуде, и она равна нулю, если расширение происходит в вакуум.

Все установленное Клапейроном справедливо только для идеальных газов. В действительности реальные газы, расширяясь в пустоту, нагреваются или охлаждаются. Это явление, известное как эффект Джоуля - Томсона, можно математически рассчитать, если уравнение Клапейрона, справедливое для идеальных газов, заменить уравнением состояния для реальных газов.

Возвращаясь к математическим расчетам отношения работы к теплоте, стоит обратить внимание на то, что это отношение по своей физической сути есть не что иное, как выражение для коэффициента полезного действия тепловой машины. Если разность температур нагревателя и холодильника записать в виде

то, сравнивая его с современным выражением

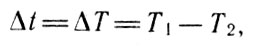
Температура

нетрудно заметить, что функция С представляет собой абсолютную температуру нагревателя.

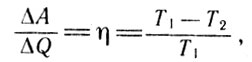
КПД (5)

В третьей главе Клапейрон теоретически доказывает, что разность между теплоемкостью при постоянном давлении и теплоемкостью при постоянном объеме одинакова для всех газов. Следует заметить, что все эти рассуждения автора проведены с использованием гипотезы теплорода.

Наиболее оригинальны рассуждения Клапейрона, проведенные им в четвертой главе. Здесь автор переносит способ расчета газов на пар, точнее, на систему "жидкость - пар" и находит вид уравнения фазового перехода.

Рассмотрим двухфазную систему "жидкость - пар" при температуре t. Начальное давление в сосуде равно bc (см. рис. 7). Приведем эту систему в контакт с телом А, температура которого также равна t. Вследствие перехода теплоты от тела к системе произойдет увеличение объема последней. Это увеличение объема cd, сопровождающееся парообразованием, будет происходить при постоянном давлении и температуре. Затем уберем тело А и, заключив систему в теплонепроницаемую оболочку, предоставим ей возможность адиабатно расширяться до объема ak. Температура при этом снизится на бесконечно малую величину Gt и примет значение t-Δt, равное температуре тела В. После этого сосуд, содержащий жидкость и ее пар, приведем в контакт с телом В и будем уменьшать объем от ak до ah. Развиваемая при этом теплота будет переходить от системы к телу В. Температура и давление в этом процессе будут сохранять неизменными свои значения.

После того как объем системы уменьшится до ah, уберем тело В, снова заключим систему в теплонепроницаемую оболочку и далее будем адиабатно уменьшать объем до значения аb. Температура газа при этом повысится на Δt и станет равной t, что соответствует ее первоначальному значению. При этом объем, занимаемый системой, примет то же значение, что и в начале цикла. Давление достигнет первоначального значения, равного bc. На этом и заканчивается полный цикл, совершаемый двухфазной системой.

Известно, что работа, развиваемая рабочим телом при переносе им теплоты от нагревателя к холодильнику, численно равна площади четырехугольника, образованного процессами, графически изображенными в осях "объем - давление". Пренебрегая бесконечно малыми второго порядка, найдем эту площадь как произведение объема cd на изменение давления dg-ek. Так как давление есть функция температуры, можем записать, используя правила дифференциального исчисления:

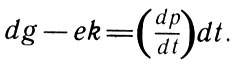
Используя правила дифференциального исчисления (6)

Отрезок cd представляет собой увеличение объема вследствие перехода жидкости в пар под давлением р при неизменной температуре.

Если обозначить Q - плотность жидкости, а б - плотность пара этой жидкости и V - объем образовавшегося пара, то произведение δV представляет собой массу образовавшегося пара, a δV /ç - объем испарившейся жидкости.

Изменение объема системы, вызванное испарением жидкости, может быть представлено выражением

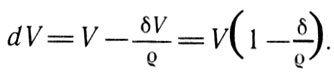
Изменение объема системы, вызванное испарением жидкости (7)

Тогда совершаемая при этом работа может быть определена как произведение

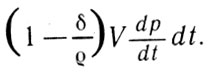
Работа (8)

Теплота, за счет перехода которой совершается работа, есть не что иное, как скрытый теплород единицы объема образовавшегося пара, или, по современной терминологии, удельная теплота испарения. Количество скрытого теплорода в единице объема этого пара (удельную теплоту испарения) обозначим k. Тогда удельную теплоту испарения пара, объем которого V, можно определить как произведение k V. Отношение совершенной работы к используемому для этого количеству теплоты может быть представлено выражением

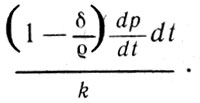
Отношение совершенной работы (9)

Эта работа, как ранее показал Клапейрон, является наибольшей, которая может быть получена с использованием единицы теплоты, и не зависит от природы рабочего тела, одинакова для газов и паров. Это же выражение с учетом (2) может быть переписано в виде

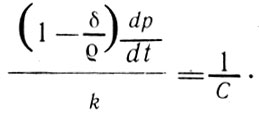
Отношение совершенной работы с учетом (2)(10)

Отсюда следует, что удельная теплота испарения данного газа может быть определена по формуле

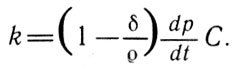
Удельная теплота (11)

Для большинства паров отношение б/о очень близко к нулю в области температур, далеких от кипения. Поэтому с большой точностью для этого случая выражение (11) можно переписать в виде

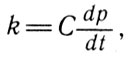
(11) с большей точностью (12)

из которого следует, что удельная теплота испарения одинаковых объемов паров некоторых жидкостей при одинаковой температуре и соответствующем давлении пропорциональна производной от давления по температуре.

Уравнение Клапейрона, обобщенное впоследствии Клаузиусом, представляет собой термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация и др.). В современной записи уравнение Клапейрона-Клаузиуса имеет вид:

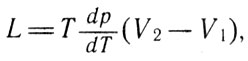
Уравнение Клапейрона-Клаузиуса (13)

где L - теплота фазового перехода; Т - температура фазового перехода (процесс фазового перехода изотермический); V₂-V₁ - изменение объема вещества при переходе его из первой фазы во вторую.

Уравнение, полученное Клапейроном, устанавливает связь между изменением давления и изменением температуры по кривой фазового перехода первого рода для чистого вещества. Важность полученного уравнения заключается в том, что, используя его, можно рассчитать наиболее трудно определяемые опытным путем величины, характеризующие состояние вещества при фазовом переходе.

Получив уравнение фазового перехода, Клапейрон рассматривает результаты, вытекающие из него, для некоторых частных случаев. Так, он пишет, что если С и ^dp/_dt имеет конечные значения, то при Q=b, k стремится к нулю, т.е. если давление велико и температура достаточно высокая, то плотность пара может быть равна плотности жидкости и, как это следует из последней формулы, удельная теплота испарения в этом случае должна быть равна нулю. Далее, удельная теплота испарения жидкости, имеющей высокую температуру кипения, например ртути, должна быть очень малой, так как для паров ртути ^dp/_dt очень мало. Эти выводы Клапейрона, как показали последующие эксперименты, вполне соответствуют действительности.

Развивая далее свои исследования, в пятой главе ученый утверждает, что вся информация, полученная им для газов и паров, справедлива и для жидкостей. Для жидкостей давление, температура, объем и количество теплорода, содержащегося в них, связаны так же, как и у газов. Математические преобразования, выполненные им, настолько громоздки и сложны, что автор, чувствуя это, вынес их в "Дополнения", помещенные в конце работы.

Одним из результатов, полученных Клапейроном, является формула для нахождения количества теплоты, развиваемой газом при изменении его состояния:

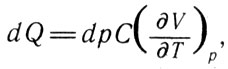
Количества теплоты (14)

где dp - изменение давления; С имеет одинаковое значение как для газов, так и для жидких и твердых тел.

Из полученной формулы следует, что для тела в любом агрегатном состоянии увеличение давления при постоянной температуре приводит к возникновению теплоты, значение

которой пропорционально изменению объема этого тела. "Это утверждение, - пишет Клапейрон, - есть общий вывод, который можно получить из основного принципа: совершенно бессмысленно полагать, что движущая сила или теплота может быть получена из ничего и безвозмездно".

В шестой главе Клапейрон вновь и вновь излагает способы, позволяющие определить вид функции С. Прямые способы решения этой задачи, к сожалению, пишет ученый, отсутствуют. Однако, имея экспериментальные данные и предлагаемый им математический аппарат, можно хотя бы приближенно найти ее значение для некоторых температур и попытаться определить характер ее изменения с температурой.

Ссылаясь на работы Дюлонга, Клапейрон утверждает, что при сжатии воздуха или другого газа, взятого при температуре t=0°С и при нормальном атмосферном давлении на ¹/₂₆₇ часть его объема, образуется теплота, которой достаточно, чтобы нагреть этот воздух на 0,421 °С. Если взять воздух массой 1 кг при нормальном давлении, объем которого равен 0,770 м³, то, используя ранее полученные уравнения, можно вычислить значение этой функции. Далее Клапейрон ставит задачу выяснить, как изменяется значение этой функции с температурой. Эти вычисления он проводит с использованием экспериментальных данных Лароша и Берара. Из их опытов следует, что в диапазоне 96,90 - 22,83°С функция С хотя и медленно, но все-таки растет.

Применяя полученное им ранее уравнение фазового перехода, он предпринимает попытку найти значение С для других температур, в частности лежащих вблизи точки кипения той или иной жидкости. Пренебрегая плотностью пара в сравнении с плотностью жидкости в полученном ранее уравнении и считая значение ^dp/_dt вблизи точки кипения примерно одинаковым для всех веществ, он находит:

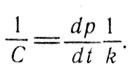
С для других температур (15)

Учитывая вышесказанное, можно предположить, что функция С тоже примерно одинакова для всех веществ, так как значение k (количество теплорода, содержащееся в равных объемах газа) - величина постоянная. Кроме того, Клапейрон использует данные экспериментов Араго и Дюлонга, поставленных для исследования скорости звука в различных газах в температурном диапазоне 100 - 224°С для установления вида и числового значения этой же функции.

Сравнивая данные, полученные различными способами, можно заключить, что ученый нашел правильный способ вычисления этого значения, но дальше на этом пути продвинуться ему не удалось. Выяснить вид функции, которая входила в выражение для коэффициента полезного действия тепловой машины, удалось позже другим ученым.

В седьмой главе Клапейрон вновь обращает внимание читателей на значение этой загадочной функции. "Эта функция, - пишет он, - может быть использована для расчета многих тепловых явлений, как тех, которые хотя и недостаточно, но все-таки исследованы, так и тех, которые пока еще не известны".

В последней, восьмой главе Клапейрон высказывает ряд соображений, касающихся непосредственно паровых машин. Здесь же он высказывает предположение, что у машин, холодильник которых находится при температуре 100°С, теплород используется не полностью, а только часть его при переходе от температуры котла к температуре 100°С; переход от 100°С до температуры окружающей среды означает потерю энергии. Наиболее выгодны те машины, утверждает он, у которых температура отработанного пара ближе к температуре окружающей среды, в которую выбрасывается пар. Для этого необходимо так проводить расширение, чтобы температура пара была равна температуре конденсатора. Все практические попытки повышения движущей силы за счет теплоты, продолжает Клапейрон, должны предусматривать именно это. Главное, отмечает ученый, не температура, а разность температур между нагревателем и холодильником. Такие же факторы, как природа рабочего тела, его агрегатное состояние, не оказывают никакого влияния на эффективность работы тепловых машин.