Энтропия и вероятность состояния

Известно, что любая система без воздействия на нее извне стремится прийти в состояние, характеризуемое минимумом ее потенциальной энергии. Эта информация позволяет в некоторой мере предсказывать направление протекания того или иного процесса в естественных условиях "без воздействия на тело или систему извне. Кроме того, как показал Клаузиус, реальные процессы всегда развиваются таким образом, что одна из важнейших характеристик состояния системы - энтропия - возрастает. Следовательно, любая термодинамическая система будет развиваться в направлении минимума потенциальной энергии и максимума энтропии. Но не только потенциальная энергия и энтропия могут помочь в определении направления протекания реальных процессов. Существует еще один, статистический, закон природы, в котором утверждается, что наиболее вероятным является состояние с максимальным беспорядком.

Рассмотрим сосуд, состоящий из нескольких соединенных между собой ячеек. Поместим в этот сосуд n молекул, которые могут свободно перемещаться по сосуду из ячейки в ячейку, распределяясь каким угодно образом. Характер этого распределения может быть самым разнообразным. В качестве примера рассмотрим распределение шести молекул в сосуде из трех ячеек. Несложные рассуждения убедят нас в том, что возможны различные способы распределения молекул по ячейкам, часть которых показана на рисунке 9. В качестве примера рассмотрим такую ситуацию. Ящик разделен перегородками на три отсека. Пусть в одном из них находятся молекулы; два других - пустые. Такую систему частиц можно считать упорядоченной. Убрав перегородки между отсеками, мы заметим, что молекулы, участвуя в хаотическом тепловом движении, через некоторое время займут весь предоставленный им объем. Наблюдая далее, мы увидим, что молекулы перераспределились так, что в каждом из отсеков содержится примерно одинаковое число молекул, хотя неизбежны и некоторые отклонения - флуктуации, которые будут тем меньше, чем больше исходное число молекул в ящике. Таким образом, система, предоставленная самой себе, приходит в наиболее вероятное состояние: одинаковое число молекул в каждом отсеке. Этот процесс перераспределения развивается в таком направлении, следуя которому энтропия возрастает; при этом система приходит к наиболее вероятному состоянию. Иначе, возрастание энтропии связано с увеличением вероятности состояния. Количественной характеристикой вероятности того или иного состояния является термодинамическая вероятность, которая представляет собой не что иное, как число способов, которыми может быть реализовано состояние данной физической системы. Распределение, соответствующее рисунку 9, является наиболее вероятным.

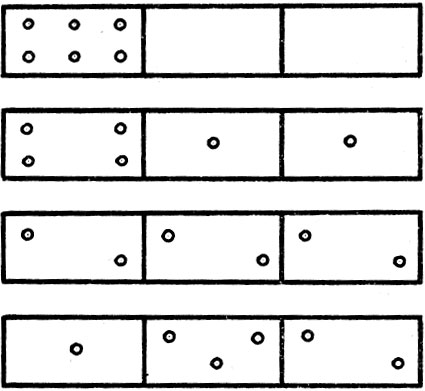
Рис. 9. Способы распределения молекул по ячейкам

Изучая термодинамические процессы, Больцман заметил общность в направлении изменения энтропии некоторой системы и в значении термодинамической вероятности состояния. Он установил, что энтропия некоторой термодинамической системы пропорциональна логарифму вероятности ее состояния. Повышение энтропии означает нарушение упорядочения, стремление системы к хаотическому движению частиц, ее образующих. Согласно теоретическим исследованиям Больцмана

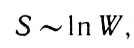
Согласно теоретическим исследованиям Больцмана (34)

где S - энтропия системы; W - термодинамическая вероятность ее состояния.

Развивая далее представления Больцмана о связи энтропии и вероятности состояния, немецкий физик М. Планк нашел коэффициент пропорциональности в соотношении (34) и получил равенство

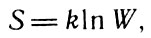
Коэффициент пропорциональности (35)

где k - константа, получившая впоследствии название постоянной Больцмана.

Из работ Больцмана и Планка следует, что второе начало термодинамики, так же как и первое, является статистическим законом. Второе начало термодинамики справедливо только для большого числа молекул, к которому можно применить статистические методы. Установленный Клаузиусом закон возрастания энтропии следует понимать как среднестатистический вывод. В отдельных частях системы могут протекать процессы, развивающиеся так, что энтропия этой части системы может убывать, хотя в целом макросистема характеризуется ростом энтропии. Эти флуктуации энергии, плотности, температуры непрерывно возникают и исчезают через сравнительно малые промежутки времени. Наиболее вероятное состояние означает то, что система находится в состоянии термодинамического равновесия. Соотношение между энтропией и термодинамической вероятностью позволяет утверждать, что энтропия представляет собой меру близости изолированной системы к состоянию термодинамического равновесия.