
§ 2. Теория предсказывает нестационарность Вселенной
Посмотрим, к каким выводам ведет факт однородного распределения вещества во Вселенной.
Важнейшей силой, действующей в мире небесных тел, является сила всемирного тяготения.
Закон, управляющий этой силой, был установлен И. Ньютоном в XVII веке.
Теория тяготения Ньютона и ньютоновская механика явились величайшим достижением естествознания. Они позволяют описать с большой точностью обширный круг явлений, в том числе движение естественных и искусственных тел в Солнечной системе, движения в других системах небесных тел: в двойных звездах, в звездных скоплениях, в галактиках.
На основе теории тяготения Ньютона были сделаны предсказания существования неизвестной ранее планеты Нептун, предсказание существования спутника Сириуса и многие другие предсказания, впоследствии блестяще подтвердившиеся. В настоящее время закон Ньютона является фундаментом, на основании которого в астрономии вычисляются движения и строение небесных тел, их эволюция, определяются массы небесных тел. Однако в некоторых случаях, когда поля тяготения становятся достаточно сильными, а скорости движения в них приближаются к скорости света, тяготение уже не может быть описано законом Ньютона. В этом случае надо пользоваться релятивистской теорией тяготения, созданной А. Эйнштейном в 1916 г.
Необходимость выхода за рамки ньютоновской теории тяготения в космологической проблеме была осознана давно, задолго до создания Эйнштейном новой теории. В последующих параграфах мы остановимся на этом подробнее, однако интуитивно и так ясно, что для вычисления поля тяготения от бесконечных масс Вселенной теории Ньютона может оказаться недостаточно.
Но оказывается, что и теория тяготения Эйнштейна, и теория тяготения Ньютона обладают одной важной особенностью, которая позволяет выяснить важнейшее свойство модели Вселенной, не прибегая к сложной теории Эйнштейна, а пользуясь исключительно теорией Ньютона. Мы потом обратимся к теории Эйнштейна и познакомимся с некоторыми ее выводами, необходимыми для полного построения космологических моделей и анализа процессов в ходе эволюции Вселенной. Такое обращение, как уже подчеркивалось, совершенно необходимо, и будет в дальнейшем обосновано. Однако если основное свойство Вселенной - ее нестационарность, - может быть понято и описано в рамках теории Ньютона, то обращение к Эйнштейну было бы просто запутыванием вопроса.
Итак, вернемся к общему важному свойству теорий Эйнштейна и Ньютона. Дело в том, что сферически-симметричная материальная оболочка не создает никакого гравитационного поля во внутренней полости. Мы здесь покажем это в случае теории Ньютона.
Рассмотрим материальную сферу (рис. 1).
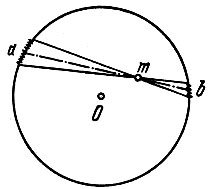
Рис. 1. Силы тяготения, с которыми площадки a и b притягивают тело m, равны по величине и противоположны по направлению
Сравним силы тяготения, которые тянут тело массы т (находящееся в произвольной точке внутри сферы) в противоположные стороны а и b. Направление линии ab, проходящей через m, произвольно. Эти силы создаются веществом, расположенным на участках сферы, вырезанных узкими конусами с одинаковыми углами при вершине. Площади площадочек, вырезаемых этими узкими конусами, пропорциональны квадратам высот этих конусов. Значит, площадь Sa площадочки а относится к площади Sb площадочки b как квадраты расстояний rа и rb от m до поверхности:
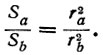
(1)
Но так как масса считается равномерно распределенной по поверхности сферы, то для масс площадочек получаем то же отношение
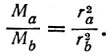
(2)
Теперь можно вычислить отношение сил, с которыми площадочки притягивают тело. Сами силы записываются согласно закону Ньютона следующим образом:
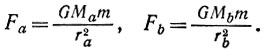
(3)
Их отношение есть
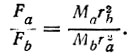
(4)
Подставляя в (4) вместо 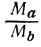 его значение из (2), находим
его значение из (2), находим
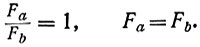
(5)
Следовательно, силы равны по абсолютной величине, направлены в противоположные стороны и уравновешивают друг друга. То же можно повторить и для любых других направлений. Значит, все противоположно направленные силы уравновешены и результирующая сила, действующая на m, равна нулю. Точка, в которой расположено тело m, произвольна. Следовательно, внутри сферы действительно нет сил тяготения.
Теперь обратимся к рассмотрению сил тяготения во Вселенной. В предыдущем параграфе было выяснено, что в больших масштабах распределение вещества во Вселенной можно считать однородным. Мы везде в этой главе будем рассматривать только большие масштабы и поэтому будем считать вещество однородным.
Выделим мысленно в этом веществе шар произвольного радиуса с центром в произвольной точке (рис. 2). Рассмотрим сначала силы тяготения, создаваемые на поверхности этого шара только веществом самого шара, и не будем пока рассматривать все остальное вещество Вселенной. Пусть радиус шара выбран не слишком большим, так что поле тяготения, создаваемое веществом шара, относительно слабо и применима теория Ньютона для вычисления силы тяготения. Тогда галактики, находящиеся на граничной сфере, будут притягиваться к центру шара с силой, пропорциональной массе шара М и обратно пропорциональной квадрату его радиуса R.
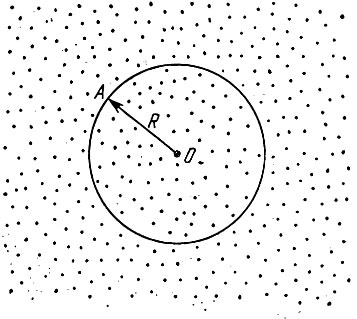
Рис. 2. Сила тяготения, с которой галактика A, расположенная на поверхности шара произвольного радиуса R, притягивается к центру шара О, определяется только суммарной массой вещества шара и не зависит от вещества, находящегося вне шара
Теперь вспомним о всем остальном веществе Вселенной вне шара, и попытаемся учесть силы тяготения, им создаваемые. Для этого будем рассматривать последовательно сферические оболочки все большего и большего радиуса, охватывающие шар. Но выше мы показали, что сферически-симметричные слои вещества никаких гравитационных сил внутри полости не создают. Cледовательно, все эти сферически-симметричные оболочки (т. е. все остальное вещество Вселенной) ничего не добавят к силе притяжения, которое испытывает галактика A на поверхности шара к его центру О.
Итак, можно вычислить ускорение одной галактики A по отношению к другой галактике О. Мы приняли О за центр шара, а галактика A находится на расстоянии R от О. Это ускорение обусловлено тяготением только вещества шара радиусом R. Согласно закону Ньютона оно есть
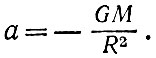
(6)
Знак минус означает, что ускорение соответствует притяжению, а не отталкиванию.
Итак, любые две галактики, находящиеся в однородной Вселенной на расстоянии R, испытывают относительное ускорение (отрицательное) а, даваемое формулой (6). Это и означает, что Вселенная должна быть нестационарной. Действительно, если бы мы представили, что в некоторый момент времени галактики покоятся, не движутся и плотность вещества во Вселенной не меняется, то в следующий момент галактики получили бы скорости под действием взаимного тяготения всего вещества, так как имеется ускорение тяготения, даваемое формулой (6). Итак, покой галактик друг относительно друга возможен лишь на мгновение. В общем же случае галактики должны двигаться - они должны удаляться или сближаться, радиус шара R (см. рис. 2) должен меняться со временем, плотность вещества должна также изменяться со временем.
Вселенная должна быть нестационарной, ибо в ней действует тяготение - таков основной вывод теории. Этот вывод, как уже говорилось во введении, был получен А. А. Фридманом на основе релятивистской теории тяготения в 1922-1924 гг. Значительно позже, в середине тридцатых годов, Э. Милн и В. Мак-Кри обратили внимание на то, что вывод о нестационарности однородной Вселенной может быть получен из ньютоновской теории по схеме, приведенной здесь.
Как конкретно должны двигаться галактики, как должна меняться плотность?
Это зависит не только от сил тяготения, управляющих движением. Эти силы дают ускорение, а точнее, торможение (знак минус в формуле (6)!), т. е. показывают, как будет меняться скорость со временем. Очевидно, надо знать, какова скорость в некоторый момент, после чего, зная ускорение, можно рассчитать, как скорость будет меняться с течением времени. Если задать в некоторый момент покой галактик, то в последующие моменты галактики начнут сближаться, Вселенная будет сжиматься. Если задать в начальный момент скорости галактик так, чтобы они удалялись друг от друга, то мы получим расширяющуюся модель Вселенной, расширение которой тормозится тяготением.
Величину скорости в некоторый момент теория тяготения сама дать не может, ее можно получить из наблюдений.
|
ПОИСК:
|