§ 2. За десять миллиардов лет до нашей эры

Как уже отмечалось в предыдущем параграфе, в этой главе мы будем заниматься процессами, происходившими в самом начале расширения Вселенной, т. е. тем, что было десять-двадцать миллиардов лет назад. Реконструкция истории Вселенной - задача, конечно, не менее трудная, чем стоящая перед археологами и историками проблема воссоздания истории древнего исчезнувшего народа по немногим ископаемым остаткам, хотя задача космологии решается другими методами. В соответствии с намеченным в конце предыдущего параграфа планом, нам предстоит перебрать разные варианты возможного характера расширения Вселенной вблизи сингулярности, с одной стороны, и различные условия в веществе в ту эпоху,- с другой, и посмотреть, к каким следствиям это ведет. Ясно, что каждый раз в нашем анализе надо менять один какой-либо параметр, чтобы быть уверенным, что изменения следствий связаны с изменением именно этого параметра.

Мы начнем с того, что будем рассматривать разные физические условия в веществе в начале расширения, а сам характер расширения (т. е. "механику" вещества) считаем пока во всех вариантах одинаковым. Будем предполагать, что и сегодня, когда мы рассматриваем достаточно большие объемы пространства, и в далеком прошлом, расширение Вселенной в точности соответствует расширению по фридмановской теории. Другие возможные варианты начала расширения мы рассмотрим в § 7 гл. 3. Решение Фридмана, продолженное в прошлое, формально дает состояние бесконечной плотности. Если в действительности в прошлом плотность вещества с большой точностью была однородной и, кроме того, движение было изотропно, то решение Фридмана применимо в прошлом вплоть до состояний огромных плотностей, пока мы наконец вблизи сингулярности не столкнемся с ситуацией, заведомо не описываемой общей теорией относительности, и требующей для своего описания другой, более общей теории.

Почему возникает необходимость такой теории? Дело в том, что современная квантовая теория предсказывает возникновение квантовых эффектов тяготения вблизи сингулярности. Теория тяготения Эйнштейна - неквантовая теория, поэтому она не может описывать эффекты, связанные с квантованием в масштабах всей Вселенной. Как можно установить условия, где необходимо учитывать квантовые эффекты тяготения? Здесь может помочь теория размерностей. Эта теория позволяет приближенно оценить параметры, где существен тот или иной процесс даже тогда, когда неизвестна детальная теория процесса, а известны только самые общие его черты, например, от каких общих явлений зависит данный процесс. Посмотрим, как работает теория размерностей в нашем случае.

Нам нужно установить радиус кривизны пространства-времени, при котором существенны следующие явления: тяготение, кванты, релятивизм (большие скорости). Роль тяготения описывается гравитационной постоянной G, роль квантов - постоянной Планка h, роль релятивизма - скоростью света с. Нас интересует радиус кривизны, т. е. величина, имеющая размерность длины, при которой существенны все три рода явлений. Теория размерности утверждает, что для этого надо составить произведение из всех трех констант, возведенных в такие степени, чтобы произведение имело размерность длины. В итоге получаем

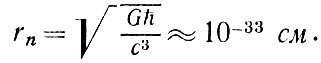
(1)

Расстояние r_n называют планковской длиной; оно ничтожно мало: r_n ≈ 10^-33 см.

Итак, квантовые эффекты в гравитации становятся определяющими, если радиус кривизны пространства - времени становится равным величине r_n. В таких условиях теория тяготения Эйнштейна уже не применима. Можно теперь вычислить, в какой момент времени после начала расширения Вселенной радиус кривизны был равен r_n и какая при этом была плотность физической материи. Первая величина получается делением r_n на скорость света с и равна t_n ≈ 10^-43 сек, а вторая оказывается равной совершенно чудовищной величине:

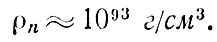
(2)

Эта плотность более чем на сто двадцать порядков больше сегодняшней средней плотности во Вселенной и почти на восемьдесят порядков больше плотности атомного ядра!

Итак, для описания процессов при t <10^-43 сек (время здесь и в дальнейшем отсчитываем от сингулярного состояния) заведомо надо строить новую теорию. К этому мы еще вернемся в гл. 4. Но применимо ли решение Фридмана при более скромных плотностях?

Во всяком случае можно быть уверенным, что общие законы физики надежно проверены при плотностях, не превышающих ядерной, ρ_яд ≈ 10^14г/_см³.

Будем считать, что решение Фридмана можно продолжить в прошлое по крайней мере до плотностей порядка ρ_яд ≈ 10^14г/_см³. Посмотрим, какие следствия вытекают из такого предположения, и сравним их с наблюдательными данными. Ясно, что в ту эпоху при столь больших плотностях не было звезд и других небесных тел. Об образовании отдельных небесных тел см. следующую главу^*. Расширяющееся вещество было, по-видимому, почти однородным. Какие процессы в нем протекали при плотности, скажем, порядка ρ_яд? На первый взгляд кажется, что процессы зависят от условий, которые были еще раньше и которых мы не знаем и поэтому . ничего не можем сказать об этих процессах. К счастью, это не так. Дело в том, что при сверхвысокой плотности все процессы превращения частиц идут весьма быстро, гораздо быстрее, чем меняется плотность вещества в ходе расширения, т. е. чем меняются условия, при которых протекают реакции. Таким образом, все реакции, какие могут протекать, успеют протечь, пока условия существенно не изменились, и вещество будет находиться в состоянии термодинамического равновесия. Это означает, что состав вещества определяется в каждый момент только условиями в этот момент, такими величинами, как плотность, температура и т. д. и, что особенно важно, никак не зависит от предшествующей истории. Это понятно, ведь все реакции идут быстро и успевают привести состав вещества в соответствие с условиями в этот момент, независимо от того, что было до этого. Расчеты показывают, что для модели Фридмана это предположение верно.

^* (O так называемых первичных черных дырах сказано в последней главе книги.)

Состояние равновесия при плотности 1014г/см3 может быть вычислено по современной теории. Наше полное незнание свойств вещества при плотности, например, 1030г/см3 (где могут играть роль и неизвестные нам частицы и проявляться неизвестные нам законы), не мешает расчету равновесия при 1014г/см3*. Конечно, для того чтобы рассчитать, что происходит в этом веществе, из чего оно будет состоять в результате быстро протекающих ядерных реакций, знания одной плотности материи недостаточно, надо знать, например, температуру и другие параметры. В общем случае таких параметров - чисел несколько. Физика утверждает, что помимо плотности вещества надо задать по крайней мере еще два параметра- числа**. Первое число характеризует, грубо говоря, степень нагретости вещества. Это знаменитая энтропия, которую так любят физики. В нашем случае энтропия вещества имеет весьма наглядный смысл. Чем больше нагрето вещество, тем больше в нем световых квантов-фотонов (и больше энергия каждого кванта). Число квантов, приходящееся на одну тяжелую частицу-барион, и характеризует степень нагретости - энтропию. Второе число - это так называемый лептонный заряд. Для нашей задачи достаточно сказать, что во Вселенной лептонный заряд характеризуется разностью числа нейтрино и антинейтрино во Вселенной, приходящихся на один барион, плюс разность числа электронов и позитронов, приходящихся на один барион***.

^* (В последние годы развитие теории элементарных частиц привело к заключению, что в самом начале расширения Вселенной, вероятно, существенны были так называемые фазовые переходы, и предыстория расширения важна. Здесь, однако, мы не имеем возможности останавливаться на этих важных уточнениях, тем более, что законченной теории пока нет. См. об этом Д. А. Киржниц. - УФН, 1978, т. 125, 169.)

^** (Говоря более строго, надо задать не два, а несколько чисел,-но нас будут здесь интересовать только два важнейших из них.)

^*** (Строго говоря, существуют два лептонных заряда - это электронный и мюонный и соответственно электронные и мюонные нейтрино. Нас сейчас интересует электронный лептонный заряд и электронные нейтрино.)

Оба числа во Вселенной, будучи заданными в один момент, остаются почти постоянными, не меняются с расширением. В этом их преимущество перед другими числами (например, температурой), которые также могли бы характеризовать состояние вещества, но меняются с расширением.

Значит, чтобы рассчитать процессы (ядерные реакции) в начале расширения, для модели Фридмана надо задать два числа: энтропию S и лептонный заряд L. Расчет ядерных реакций позволяет предсказать химический состав вещества, из которого формируются галактики, звезды, межзвездный газ. Сравнение предсказания с наблюдениями выявит истинные условия в прошлом.