
§ 3. Эволюция малых возмущений в горячей Вселенной
Начнем с рассмотрения эволюции малых возмущений в виде сгустков материи, т. е. адиабатических возмущений.
Интуитивно кажется наиболее естественным считать их ответственными за происхождение галактик. Во всяком случае исторически, как мы видели, эта идея восходит еще к Ньютону.
Мы должны применить идею гравитационной неустойчивости к расширяющейся горячей Вселенной. Теория гравитационной неустойчивости Джинса была развита применительно к расширяющейся Вселенной Фридмана Е. М. Лифшицем в СССР в сороковых годах. Эта работа явилась основополагающей для всех дальнейших исследований по происхождению структуры Вселенной.
Теория происхождения галактик в результате адиабатических возмущений в горячей Вселенной была особенно подробно развита в СССР школой академика Я. Б. Зельдовича. Посмотрим, как горячая однородная расширяющаяся среда может распасться на части. Критическая длина Джинса зависит от плотности среды и скорости звука в ней (см. формулу (7)). Поэтому можно вычислить ее для каждого момента времени в расширяющейся Вселенной. Мы уже видели выше, что на ранних стадиях расширения главную долю массы расширяющейся среды составляет свет. Давление среды также определяется давлением света. Световые частички - кванты - движутся с предельными возможными в природе скоростями. Поэтому давление среды, определяемое этими скоростями, очень велико. Велика и скорость звука, которая составляет около половины скорости света. А значит, велика и критическая длина Джинса, которой мы сейчас интересуемся. Она оказывается примерно равной горизонту видимости (см. § 5 гл. 2), т. е. расстоянию, которое свет проходит за все время с начала расширения Вселенной до рассматриваемого момента времени.
Этот вывод легко получить, заметив, что в формуле (7) скорость звука на ранних этапах расширения мира примерно равна скорости света vзв ≈ с, а величина √(1/8/3πGρ) примерно соответствует, согласно теории Фридмана, времени расширения Вселенной от сингулярного состояния до состояния, когда плотность вещества равна ρ (см. формулы (8) и (9).в § 5 гл. 3). В результате получаем
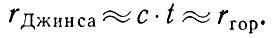
(8)
Полученный вывод чрезвычайно важен. Как мы сейчас увидим, он означает, что в этих условиях рост первоначально малых возмущений не приводит к распаду среды на отдельные тела. Нам придется рассматривать области размером больше критического (см. § 12 гл. 1), когда нужно учитывать релятивистские эффекты. По необходимости мы будем в нашем разъяснении пользоваться приближенными понятиями и аналогиями, так как не можем использовать здесь в кратком описании сложный аппарат релятивистской теории.
Пусть в однородной расширяющейся среде Вселенной были небольшие случайные уплотнения. Расти могут только уплотнения, имеющие размер больше джинсовской длины, т. е. в нашем случае больше горизонта видимости. Под действием тяготения эти уплотнения увеличиваются. Рассмотрим одно из таких уплотнений. Его край* под действием тяготения, связанного с уплотнением, движется относительно невозмущенной системы отсчета к центру уплотнения. Конечно, край не может двигаться со скоростью, большей скорости света, а в действительности движется (по отношению к невозмущенной системе отсчета) со скоростью много меньшей световой. Это значит, что за время, протекшее с начала расширения, край уплотнения продвинется лишь на небольшую долю размера уплотнения. Ведь размер уплотнения больше горизонта видимости, а только свет за время расширения успевает пройти такое расстояние. Раз край уплотнения сдвинется за все время расширения Вселенной на небольшую величину, значит, плотность в уплотнении возрастет незначительно, и уж, конечно, сгущение не успевает вырасти настолько, чтобы превратиться в изолированное тело**.
* (Мы для простоты говорим кратко "край уплотнения". На самом деле резкого края у возмущения, вообще говоря, нет, оно плавно спадает и переходит в окружную среду. Понятие "край" приближенное. Но мы предупреждаем читателя, что разъясним главное свойство процесса, оставляя в стороне многие детали.)
** (В самом предельном случае, когда гравитационное поле возмущения очень велико (точнее, на языке релятивистской теории, когда искривление пространства в масштабе уплотнения велико), возмущение успевает как раз к моменту, когда его размер порядка горизонта (но не раньше этого момента!), вырасти настолько, что становится большим (т.е. плотность среды в нем заметно больше средней плотности окружающей среды) и начинает сжиматься. Но тогда размер неоднородности порядка ее гравитационного радиуса (см. § 1 гл. 2) и происходит образование так называемой первичной черной дыры. Об этом мы еще будем говорить в §7 гл. 5.
Сейчас еще раз подчеркнем, что это возможно, если искривление пространства (т. е. поле тяготения) было с самого начала в области возмущения намного больше, чем в окружающей среде.
Если же возмущение по всем параметрам - по избытку плотности, по скоростям движения среды относительно невозмущенной системы отсчета и по кривизне пространства - было малым, то оно не успевает стать большим к моменту, когда размер его стал порядка горизонта.)
Таким образом, на ранних этапах расширения, когда давление определяется давлением света, сгущения, имеющие размер больше горизонта видимости, хотя и растут, но растут медленно и не успевают выделиться в отдельные тела. Что же произойдет с возмущением после этого момента? Для этого обратимся к рис. 29. Здесь по горизонтальной оси отложено время, по вертикальной оси масса возмущенной области. При этом мы учитываем только массу обычного вещества и не учитываем массу света, ибо галактики образуются из обычного вещества. На рисунке нанесена линия Мджинса, показывающая, какую массу вещества охватывает в каждый момент времени сфера радиуса rджинса. Возмущения, имеющие в данный момент массу больше, чем масса Mджинса (т. е. на рисунке выше линии Мджинса), растут, меньше Мджинса (ниже линии Мджинса) - не растут. Об остальных линиях на рисунке сказано чуть позже. Теперь мы можем проследить за судьбой любого возмущения определенной массы. Проведем горизонтальную линию С, соответствующую этой массе. Как видно из рисунка, в ранний период это возмущение растет до момента t1 пересечения горизонтали С с линией Мджинса. Мы уже знаем, что хотя возмущение росло, но к этому моменту оно еще мало. После t1 масса возмущения меньше массы Мджинса и роста возмущения не происходит. Оно превращается в акустические колебания. Можно показать, что при этом амплитуда акустических колебаний остается постоянной - не нарастает и не уменьшается, если не учитывать затухание из-за вязкости. Вязкость обусловлена тем, что вещество хотя и непрозрачно для света, но постепенно фотоны все же сквозь него "продираются". Вязкость по-разному сказывается на крупномасштабных и мелкомасштабных возмущениях. Все мелкомасштабные возмущения затухают. Крупномасштабные остаются. К количественной характеристике мы вернемся позже.
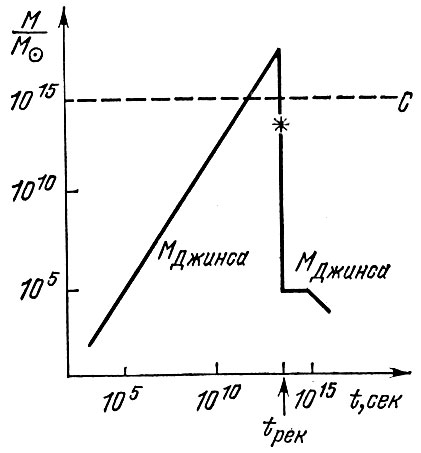
Важные изменения наступают, когда температура в расширяющейся Вселенной упадет до 4 тысяч градусов. При этой температуре происходит, как описано в § 9 гл. 3, превращение ионизованной плазмы, которой было вещество Вселенной при более высокой температуре, в нейтральную среду. Больше нет плазмы - есть нейтральное вещество. Это кардинальным образом меняет ситуацию с возможностью роста сгущений. Дело в том, что когда вещество стало нейтральным, оно стало прозрачным для света. Раньше именно давление света обеспечивало упругость среды, делая критическую длину Джинса очень большой. Теперь свет не играет роли в упругости вещества: при росте сгущений он свободно выходит из них. Только обычное газовое давление теперь противостоит силе тяготения. Но это давление оказывается много меньше светового, скорость звука в нейтральном веществе много меньше световой и длина волны Джинса резко уменьшается. Это показано на рисунке 3. Давление вещества меньше, чем давление излучения в тот же момент во столько раз, во сколько число частиц обычного вещества меньше числа фотонов, т. е. в nγ/nr ≈ 109 раз; скорость звука в √(109) раз меньше, во столько же раз меньше джинсовская длина волны, а Мджинса уменьшается в (109)3/2 раз. Сразу после рекомбинации Мджинса ≈ 105 М .
.
Теперь все неоднородности с массой больше Мджинса ≈ 105 M могут расти из-за гравитационной неустойчивости. Длина волны Джинса теперь много меньше rгор, поэтому теперь возмущения могут, вырастая, стать большими и превратиться в обособленные тела.
могут расти из-за гравитационной неустойчивости. Длина волны Джинса теперь много меньше rгор, поэтому теперь возмущения могут, вырастая, стать большими и превратиться в обособленные тела.
Как идет процесс дальше, мы разберем в следующем параграфе. Здесь же напомним, что к моменту рекомбинации сохранились не все возмущения. Мелкомасштабные возмущения затухли из-за вязкости, когда перед рекомбинацией они были акустическими колебаниями. Расчет показывает, что к моменту конца рекомбинации затухнут все возмущения с массой меньше, чем 1013 M или 1014 M
или 1014 M . Она отмечена на рис. 29 звездочкой.
. Она отмечена на рис. 29 звездочкой.
Обратимся теперь к другим типам возмущений.
Особенно просто рассмотреть поведение энтропийных возмущений. Эти возмущения до рекомбинации не могут ни расти, ни затухать. Неоднородности вещества "вкраплены" в однородный фотонный газ, в реликтовое излучение, и расширяются вместе с ним. После рекомбинации вещество освобождается от излучения и неоднородности могут расти под действием гравитационной неустойчивости, разумеется, если их масса больше Мджинса ≈ 105 М .
.
Несколько сложнее обстоит дело с вихревыми возмущениями. Посмотрим прежде всего, как меняется скорость движения среды в таких возмущениях с расширением Вселенной. Во вращательном движении сохраняющейся величиной является момент импульса массы, который по порядку величины равен M*R*v, где М - масса возмущенной области, R - ее размер, v - вихревая скорость. Подставим в это выражение вместо массы М ≈ R3ρ и если теперь вспомним, что плотность р для реликтового излучения меняется как R-4 (см. § 5 гл. 3), то мы придем к заключению, что из неизменности момента импульса следует постоянство вихревой скорости v. Итак, до момента, когда плотность среды определяется светом, т. е. практически до момента tрек, вихревые скорости остаются неизменными. Для этого типа возмущений применимы те же соображения о затухании скорости из-за вязкости, что и для адиабатических возмущений. Расчет показывает, что к моменту рекомбинации затухают вихревые движения с массой в 4*1011 M и меньше.
и меньше.
До рекомбинации вихревые движения происходят без возникновения неоднородностей плотности. Сразу после рекомбинации скорость звука в среде падает, как мы видели, в √(109) раз, и вихревые скорости становятся сверхзвуковыми. Они генерируют возникновение сгустков, а сгустки будут нарастать за счет гравитационной неустойчивости, как выяснено выше.
Имеется еще одно важное свойство у вихревых возмущений. Будем следить за поведением этих возмущений в прошлом, приближаясь к сингулярности. Из рисунка 29 видно, что достаточно рано любое возмущение существенно превышает по размерам горизонт видимости. А это ведет к тому, что надо учитывать релятивистские эффекты тяготения, связанные с вращательными скоростями этой массы. Оказывается, что эти релятивистские эффекты вблизи сингулярности столь велики, что силь-лейшим образом меняют сам характер космологического расширения. Иными словами, для того чтобы на более поздних этапах были вихревые возмущения, расширение в самом начале должно проходить не по Фридману. Это сразу же делает маловероятным предположение о том, что вращательные возмущения ответственны за происхождение галактик. Правда, молодой советский астрофизик Г. В. Чибисов показал, что от этой неприятности вблизи сингулярности можно избавиться, если предположить, что в ту эпоху навстречу вихревым потокам фотонов движутся вихревые потоки гравитонов, так что суммарный вихрь равен нулю. Но такая картина не представляется естественной, хотя она и возможна в принципе.
|
ПОИСК:
|