§ 6. Возможность сложной топологии Вселенной

В § 3 гл. 2 мы уже кратко обсуждали вопрос о том, что топологические свойства Вселенной могут быть сложными.

Вопрос о структуре мира как целого является одной из важнейших проблем, лежащих на грани между естественными науками и философией. Этот вопрос получил новый смысл, новое содержание в начале века в связи с созданием теории относительности.

До этого считалось самоочевидным, что пространство является евклидовым трехмерным, а время течет везде одинаково. Специальная теория относительности изменила это наивное (с сегодняшней точки зрения) убеждение, - пространство и время оказались объединенными в единое четырехмерное многообразие. Конкретным выражением этого объединения явилось установление закона преобразования координат и времени при переходе к движущейся системе отсчета.

Однако в вопросе о структуре мира создание специальной теории относительности дало удивительно мало! Возникло представление о четырехмерном псевдоевклидовом многообразии (пространство Минковского), в котором можно по-разному выбирать ось времени t и соответствующее ортогональное трехмерное многообразие - "пространство". Однако в этой картине по-прежнему не возникает сомнения в том, что время и каждая из трех пространственных декартовых координат в жесткой инерциальной системе отсчета могут изменяться от -∞ до +∞. Специфические свойства пространства Минковского приводят к тому, что сохраняется понятие абсолютного прошлого и абсолютного будущего. Не возникает специально вопрос о топологии пространства - времени^*. До создания общей теории относительности проблема структуры Вселенной понималась как пространственное распределение и эволюция вещества и полей, наполняющих Вселенную. Структура самого пространства (и времени) казалась самоочевидной.

^* (Формально вопрос о топологии пространства можно поставить и в ньютоновской физике. Речь идет о специальных побудительных причинах постановки такого вопроса.)

В схематическом изложении выше в этом параграфе мы не упоминали о высказываниях Лобачевского, Больяи, Римана, о неопубликованных идеях Гаусса; глубокие идеи творцов неевклидовой геометрии, как мы уже говорили в § 1 гл. 2, предвосхищали в этом вопросе ОТО, эти идеи будут обсуждаться ниже в рамках ОТО. Итак, именно ОТО поставила вопрос о структуре самого пространства и времени.

Этот вопрос необычайно труден и для теоретического и для экспериментального исследования. Мы вынуждены ограничиться в этой книжке лишь самыми простыми замечаниями и примерами, показывающими, однако (хотя бы упрощенно), всю глубину и необычность проблемы, о которой еще недавно даже не задумывались, а многие предпочитают не думать и сегодня.

Обратимся к масштабу, в котором сейчас ведутся астрономические исследования. В этом масштабе (порядка 10²⁸ см), как мы видели в § 2 гл. 2, велико искривление пространства-времени.

Именно возможность большого искривления пространства-времени, т. е. существенного отклонения его глобальных свойств от евклидовых, естественно и неизбежно приводит к вопросу о топологии пространства-времени.

В случае однородной и изотропной модели мы уже столкнулись с этим вопросом в § 3 гл. 2 при обсуждении случая плотности больше критической, ρ > ρ_крит. В этом случае трехмерное пространство оказалось замкнутым, конечным, хотя и безграничным.

Итак, есть случай, когда топология, отличная от евклидовой, необходима. Дальше следует естественное обобщение: можно искать возможные топологические неевклидовы модели и в том случае, когда необходимыми они не являются. Простейший пример такого пространства построен на рис. 19. Мы построили там пример плоского двумерного многообразия с топологией, отличной от обычной: замкнутого в одном направлении и бесконечного в другом. Очевидно, подобный пример можно построить и с плоским трехмерным пространством. Возможны и более сложные примеры. Так, выделим в плоском трехмерном пространстве параллелепипед и отождествим ("склеим", как мы делали в § 3 гл. 2 с полоской из плоскости) его противоположные стенки. Получится замкнутое трехмерное плоское пространство. Этот случай называется "трехмерным тором".

Таким образом, можно предположить, что существует плоское замкнутое трехмерное пространство. Следует подчеркнуть, что при выполнении указанных отождествлений мы имеем дело именно с замкнутым плоским пространством, а не с периодически повторяющейся структурой в неограниченном плоском пространстве. Это значит, что в этом случае в мире существует ограниченное количество галактик, а не повторяющийся до бесконечности набор одинаковых совокупностей галактик. Такой мир не имеет границ и разрывов. В этом случае наблюдения дают много изображений, "духов", соответствующих каждому объекту данного типа, который одновременно виден с разных сторон и в разные моменты времени за счет того, что свет много раз успевает обойти такой замкнутый мир за время расширения. В принципе ситуация не отличается от предсказаний теории сферического замкнутого мира - модели Леметра с космологической постоянной (см. § 12 гл. 1). Напомним, что специальные поиски совпадающих объектов в противоположных участках неба, предпринятые в связи с этой моделью, не привели к положительному результату.

Несколько более сложным примером, чем "трехмерный тор", является так называемое эллиптическое пространство постоянной положительной кривизны. Чтобы понять, что это такое, обратимся снова к двумерной аналогии. Возьмем сферу - двумерное пространство постоянной положительной кривизны. Проведем у сферы экватор и отбросим верхнюю половину сферы. Осталась только нижняя половина сферы. Теперь отождествим ("склеим") противоположные точки экватора у оставшейся половины (рис. 33). Мы получим замкнутое "эллиптическое" двумерное пространство. Здесь наглядно его представить нам почти невозможно даже несмотря на его двумерие. Но математика утверждает, что такое многообразие возможно! Площадь "эллиптической" сферы есть ¹/₂ площади сферы. Аналогичное построение возможно и для трехмерного пространства постоянной положительной кривизны. На каждом шагу число измерений при этом увеличено на единицу. Конечно, наглядное представление теперь вовсе затруднительно. Объем эллиптического пространства составляет половину объема сферического пространства.

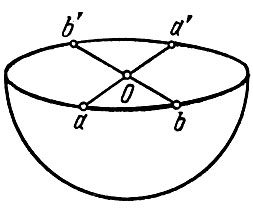
Рис. 33. Половина сферы при отождествлении диаметрально противоположных точек экватора, а с а', b с b' и т. д. превращается в эллиптическую сферу

Как мы уже неоднократно говорили раньше, при обсуждении искривленных пространств не надо представлять их реально вложенными в пространство большего числа измерений. Вне Вселенной ничего нет. Мы сейчас не говорили о четвертой координате - о времени. На самом деле все время речь должна идти не только о трехмерном пространстве, но о четырехмерном пространстве-времени и его топологии.

Все сказанное показывает необходимость специального исследования топологии пространства-времени Вселенной. Количество различных топологических вариантов четырехмерного пространства-времени необычайно велико, и на первый взгляд в космологии открывается огромное количество возможностей. Мы отсылаем за подробностями к книгам: Пенроуза "Структура пространства-времени" и Хоукинга, Эллис "Крупномасштабная структура пространства-времени". В действительности уже минимальная информация о фактических свойствах Вселенной сильно ограничивает безбрежный простор топологических структур. Но, что особенно важно, теория эволюции Вселенной оказывается почти не зависящей от топологии. Именно этим и объясняется сравнительно малое число серьезных работ по данному вопросу.

Рассмотрим теперь модель пространственно-однородного мира. Отметим прежде всего, что условие пространственной однородности выделяет в четырехмерном пространстве-времени "параллельные" трехмерные многообразия (пространства в разные моменты времени, с разной плотностью вещества в них и т. д.), на которых осуществляется однородность, и ортогональную к ним одну определенную ось времени. По оси времени "отождествления" (такие, как описаны выше для параллелепипеда в трехмерном пространстве), вероятно, запрещены законами физики и исключаются. Этот запрет обосновывают обычно принципом причинности. Действительно, пусть на оси времени t₂ > t₁ После отождествления t₂ = t₁ оказывается, что будущее и прошлое выделены только локально, а в целом, глобально, они перепутаны. Вмешательство в физические явления в момент t₂ в точке х вызывает изменения в момент t₁ в той же точке х, т. е. в прошлом.

На самом деле замкнутость линий времени может носить гораздо более "хитрый" характер, чем в рассмотренном простейшем примере. Могут, например, замыкаться не все линии времени, а только некоторые (при отсутствии однородности). Подробности см. в упомянутых выше книгах Пенроуза и Хоукинга и Эллис. Здесь же мы отметим, что соотношения между замкнутостью линий времени и принципом причинности отнюдь не столь тривиальны. По-видимому, из замкнутости линий времени вовсе не однозначно следует нарушение принципа причинности, ибо события незамкнутой линии времени уже "самосогласованы". Они все влияют друг на друга по замкнутому циклу, и в этом смысле причинная связь сохраняется.

Однако в космологии при учете однородности по пространству и необратимости эволюции можно, вероятно, запретить любое отождествление по времени. В самом деле, с течением времени монотонно растет удельная энтропия (на один барион или на единицу, сопутствующего пространства). Монотонно убывает в результате ядерных реакций доля протонов в среднем составе Вселенной. Уже по этим причинам ситуация в более поздний момент t₂ не тождественна ситуации в момент t₁

Став на эту точку зрения, мы должны заключить, что применительно к оси времени остается лишь вопрос о том, простирается ли шкала: 1) от - ∞ до + ∞, или 2) от t₁ до + ∞ , или 3) от - ∞ до t₁, или 4) от t₁ до t₂. Для однородных моделей ответ на этот вопрос получается путем интегрирования уравнений эволюции. Хотя в настоящее время наблюдательные данные и отвергают варианты 1) и 3), но не позволяют выбрать между вариантами 2) и 4). Здесь под "началом" и "концом" шкалы времени подразумеваются сингулярные состояния^*. Итак, вопрос о топологии мира сузился до топологии трехмерного пространства.

^* (Еще раз напомним: вопрос о том, что было "до" сингулярности в .начале расширения или что будет "после" сингулярности, следующей за сжатием (вариант 4), не может пока быть решен в рамках существующих физических теорий. В сингулярности возникают квантовые эффекты тяготения, вероятно, перестают быть применимыми понятия непрерывного метрического пространства - времени, возможно, лишаются смысла или изменяются понятия "до" и "после" и т. д. Исследование всего этого - дело будущего.)

При этом все еще остается значительное число разных топологических вариантов: существуют 18 топологических вариантов плоского трехмерия и бесконечное число (!) вариантов гиперболического изотропного трехмерия постоянной отрицательной кривизны.

Анизотропия мира, если такая была в начале расширения при сохранении однородности, - дополнительно ограничивает число возможных топологических вариантов. Этот вывод наглядно очевиден: при всяком отождествлении двух поверхностей или (что практически то же самое) при обходе по каждому циклу, характеризующему топологический вариант, в изотропной модели достаточно тождества "скалярных" величин, таких как плотность вещества и т. д., а это тождество обеспечивается условием однородности^*. В анизотропном мире после обхода нужно вернуться в исходную точку с теми же значениями векторных и тензорных величин, с теми же направлениями скорости вещества, главных осей деформации и главных осей тензора кривизны пространства.

^* (Как известно, законы физики не инвариантны относительно зеркального отражения трехмерного пространства. Поэтому нужно различать скаляры и псевдоскаляры. Обход по циклу не должен превращать правую систему в левую, Это условие устраняет часть топологических вариантов.)

Обратимся к задаче об эволюции. Важнейший факт заключается в том, что в однородной космологии уравнения эволюции для локальных величин не зависят от топологического варианта, температура, плотность меняются со временем по одинаковому закону для всех вариантов.

Следовательно, анализ протекания ядерных реакций и многих аналогичных процессов в однородной Вселенной - или, точнее, во всех топологических вариантах модели однородной Вселенной,- оказывается cтрого независимым от топологических свойств модели. Топология модели существенно влияет, однако, на решение более общей задачи. Так, например, топология существенно влияет на глобальное распространение сигналов. Появление "духов" - многократных изображений данного объекта в некоторых топологических вариантах при многократном обходе светом мира - это пример влияния топологии на распространение света.

По подобным наблюдательным предсказаниям можно в будущем пытаться выяснить истинную топологию Вселенной. Мы вынуждены ограничиться здесь этими краткими замечаниями о топологии Вселенной. "Привычно" все же считать, что реальная Вселенная имеет простейшую топологию. Может быть, под слово "привычно" будущие исследования подведут более надежный научный базис. Сейчас это один из "горячих" вопросов космологии.

Хотелось бы все же подчеркнуть, что указанные здесь возможности (и другие, гораздо более сложные и глубокие, которых мы не смогли коснуться) не являются просто плодом фантазии изощренного ума (или даже горячечного бреда) теоретиков. Мы знаем, что очень многие совершенно "безумные" идеи теоретиков в нашем веке оказывались самой настоящей реальностью. Но надо твердо помнить, что все "безумства" науки основаны не на пустых фантазиях (которыми, к сожалению, отличаются часто "творцы" доморощенных гипотез, не утруждающие себя серьезными знаниями и работой в науке), а на глубоких и сложных знаниях и проникновении в тайны природы.