IV. Письма и волны

48. Да будет свет!

А Наступают сумерки. Где-то в начале улицы замыкают рубильник, и все нити накальных ламп вспыхивают. Но почему они вспыхивают неодновременно? Сначала ближний фонарь, а затем следующий и т. д., причем каждый позже предыдущего, так что создается впечатление бегущей вдоль по улице волны поджига^*). Почему?

^*) (Автор признателен инженеру А. Громову за идею этой задачи и за проделанные в нашей лаборатории эксперименты.)

Б - Запаздывание из-за конечной скорости света? Но его скорость такова, что улицу длиной в 1 км он пробегает за 3,3 мкс. " А инерция зрения в 20 000 раз больше, так что заметить это невооруженным глазом невозможно.

- Но надо еще учесть и время движения волны тока по проводам. Запаздывание равно сумме запаздываний движения тока туда и света обратно.

Верно, но скорости тока и света практически равны (если не делать специальных индуктивно-емкостных замедлителей). Время запаздывания всего лишь удвоилось бы.

Кроме того, если вы посмотрите в другой конец улицы (на другой вечер, конечно), то обнаружите, что волна зажигания бежит на вас, а не от вас. А это полностью разрушает приведенное выше объяснение. Оба конца улицы одновременно вы можете увидеть, находясь в стороне от нее. Волна будет бежать со стороны рубильника. Если он слева, то волна будет бежать по фонарям вправо, сначала приближаясь к вам, а затем удаляясь.

Одна из главных причин запаздывания - инерция накальной нити лампы: пока она не разогреется - света не будет. Но почему, несмотря на однотипность всех ламп и одинаковость их инерции, загораются они не одновременно?

В На рис. 55 показана идеализированная двухпроводная линия и множество накальных ламп. Подав напряжение, мы обнаруживаем, что все лампы вспыхивают одновременно (пренебрегаем упомянутыми микросекундами).

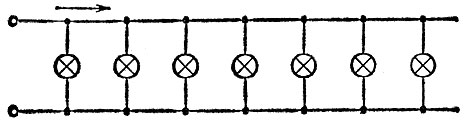
Рис. 55

Однако если перейти от идеальной линии к реальной, сразу обнаруживаются существенные различия; каждый погонный метр провода обладает сопротивлением ρ, индуктивностью L и емкостью С (емкость образуется главным образом за счет двухпроводности: два провода - это две обкладки "конденсатора"). На частоте сети (очень низкой - 50 Гц) влиянием индуктивности и емкости на выводы нашей задачи можно пренебречь. Но сопротивление проводов, которое тоже, казалось бы, пренебрежимо мало, является, ко всеобщему удивлению, решающим.

На рис. 56 показана схема, эквивалентная реальной линии с семью фонарями. Здесь R - сопротивление накальной нити лампы, г - сопротивление провода от фонаря до фонаря. Из схемы следует, что поскольку сопротивления проводов г включены последовательно с сопротивлением лампы R, то, если подать на вход напряжение Е₀ = 220 В, к лампе 6 будет приложено U₆ < E₀, так как часть напряжения упадет на обоих r. Легко убедиться, что на рис. 56 E₀ > U₆ > U₅ >...> U₀, т. е. самая далекая лампа будет и самой тусклой.

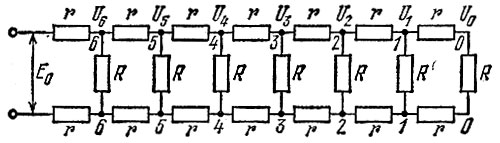
РИс. 56

Однако не думайте, что в этом все дело! Объяснением бегущей волны поджига тут еще и не пахнет!

Главная причина бегущей волны в том, что сопротивление накальной нити в холодном состоянии Rx намного меньше, чем в горячем (R_X << R_Г). В момент включения все лампы холодны. Рассмотрим одну-единственную лампу 6 (рис. 56). Напряжение E₀ прикладывается к делителю напряжения r + R^x + r, и поскольку R_x мало, то ток велик и на сопротивлениях проводов падает значительная часть напряжения. В результате на самой лампе U_6х << Е₀. Но ведь это напряжение является исходным для делителя, в состав которого входит вторая лампа 5. Эта лампа тоже холодна и ее R_x мало, а значит, U_5x << U_6x. Более того, второй делитель 6-5-5-6 шунтирует первую лампу 6, отчего сопротивление между точками 6-6 и напряжение U_6x еще меньше. И вот такое низкое напряжение U_6x прилагается к делителю 6-5-5-6, еще более низкое напряжение

U_5х - к делителю 5-4-4-5 и т. д. В результате последняя лампа O разогревается малым током I₀ от малого напряжения U₀ а первая 6 - большим током I₆ от большого напряжения U₆. Ясно, что первая от рубильника лампа разогревается быстрее. И вот тогда произойдет самое интересное. Сопротивление горячей лампы раз в десять больше сопротивления холодной. Поэтому первая лампа практически перестает шунтировать последующие: ток в ней уменьшается, уменьшится и падение напряжения на подводящих проводах, отчего возрастет падение напряжения на лампе U₆. (Ток уменьшился, а падение напряжения возросло - это не нарушение закона Ома, потому что сопротивление лампы переменно: оно возросло больше, чем напряжение на ней.)

Итак, в горячем состоянии лампы 6 напряжение U_6Г >> U_6x, а поскольку U_6Г подается на делитель 6-5-5-6, то создаются условия для разогрева лампы 5, все еще шунтирующей последующие лампы. В соответствии с этим каждая последующая лампа загорается после того, как загорелась предыдущая.

Итак, гвоздем задачи являются два неравенства:

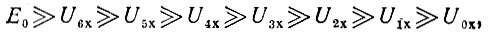
(1)

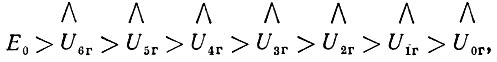
(2)

а точнее, неравенство этих неравенств (отражено несколько непривычно, с помощью знаков ∧ между членами верхнего и нижнего неравенств). Неравенство (1) для холодного состояния значительно сильнее неравенства (2), соответствующего горячему состоянию. Промежуточное состояние между этими двумя крайними особенно интересно:

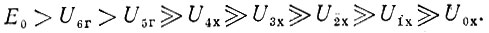
(3)

Здесь отражено состояние, когда лампы 6 и 5 уже горят, их сопротивления уже велики, и поэтому U₆ и U₅ уже незначительно отличаются от E₀ (знак >), а остальные еще не горят, их сопротивления еще малы, и поэтому U_4х, U_3х и т. д. отличаются от своих предшественников значительно (знак >>). По мере перехода из состояния (1) в состояние (2) знаки ^заменяются на знаки >, но не все одновременно, а по очереди, слева направо. Это и обеспечивает движение волны поджига по улице слева направо.

От изложенного выше чисто качественного решения задачи следует перейти к количественному, иначе среди читателей найдутся скептики, сомневающиеся в том, что сопротивление r, обычно довольно малое, может привести к заметному эффекту.

Алюминиевый провод сечением 1,5 мм² длиной 50 м имеет сопротивление r = 1 Ом. Сопротивление накальной нити лампы на 220 В и 100 Вт зависит от температуры, которая, в свою очередь, зависит от напряжения. Для установившегося режима (спустя, например, минуту после включения напряжения), т. е. после того как лампа прогрелась до максимума, соответствующего данному напряжению U, эксперимент дает цифры тока I, сопротивления R и относительной светоотдачи L, указанные в табл. 1.

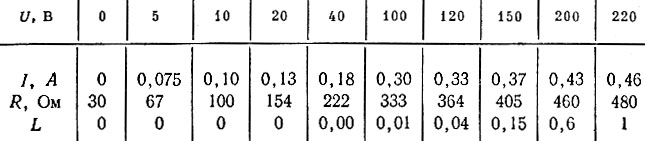
Таблица 1

Итак, R_x = 30 Ом, R_г = 480 Ом, т. е. сопротивление нити после включения под напряжение 220 В возрастает в 16 раз.

В табл. 2 показаны результаты расчета сопротивлений схемы между точками i-i и падения напряжения на них в момент включения (U_ix) и после разогрева всех ламп (U_iг). Считать R_i удобнее от конца к началу схемы, U_i - от начала к концу. Строка U_ix иллюстрирует сильное начальное неравенство напряжений на лампах (неравенство (1)), строка U_iг - слабое конечное неравенство (2).

Таблица 2

Этот расчет показывает, что в момент включения на ближайшей лампе возникает напряжение 175 В, вполне достаточное для ее разогрева до свечения (спустя время, определяемое тепловой инерцией нити), а на последней лампе в этот же момент возникает всего лишь 63 В, которые не заставят светиться лампу, рассчитанную на 220 В. Она загорится гораздо позже, когда все предыдущие лампы перестанут ее шунтировать. После этого на ней установится 197 В, что достаточно для ее свечения, правда, несколько более слабого, чем при 220 В.

Как же идет у каждой лампы переход из начального состояния в конечное? Рассчитать сам переход в рамках данной книги невозможно. Дело в том, что законы роста напряжения на каждой лампе различны, и поэтому различны законы роста температуры каждой нити и, следовательно, ее сопротивления. А каждое из этих растущих сопротивлений, в свою очередь, влияет на рост напряжения на каждой из ламп, как последующих, так и предыдущих. Кроме того, рост температуры не повторяет рост напряжения ни по форме, ни по времени из-за тепловой инерции нити. И, наконец, светоотдача нити определяется через спектральную характеристику глаза и совпадающую с нею часть спектра излучения нити, которая сростом температуры долго пренебрежимо мала (см. строку L в табл. 1), а затем начинает расти гораздо круче напряжения. Короче говоря, для строгого решения задачи о свечении каждой из семи ламп в за* висимости от времени необходимо решение системы из семи дифференциальных уравнений, которую читатель может решить на досуге, когда поступит в аспирантуру. Мы же вполне удовлетворим свое любопытство, сняв интересующие нас кривые экспериментально (рис. 57), с помощью специальной настольной модели (рис. 58), в которой вместо сопротивлений длинных проводов поставлены компактные резисторы 2r.

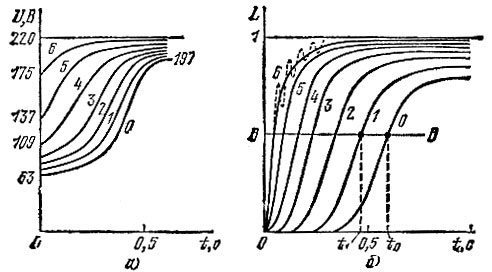
Рис. 57

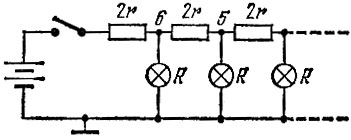
Рис. 58

Если вы вместо аккумулятора будете питать модель от сети, то все кривые станут знакопеременными, однако амплитуды этих синусоид будут меняться в соответствии с рис. 57, а. Изменится и рис. 57, б, но не столь решительно: появятся пульсации света с глубиной не более 10-15% (пунктир на кривой 6), так как тепловая инерция нити не позволяет падать яркости лампы до нуля в моменты перехода напряжения через нуль (см. следующую задачу).

Подытожим: для того чтобы увидеть бегущую по фонарям волну поджига, необходимо наличие трех условий: заметного сопротивления проводов, тепловой инерции накальных нитей ламп и зависимости сопротивления нити от ее температуры. Отсутствие любого из этих условий ведет к одновременности зажигания всех ламп. В случае накальных ламп все три условия присутствуют всегда. Правда, в разных случаях - в разной степени. В хорошо сконструированной линии сопротивление провода от фонаря до фонаря меньше 1 Ом. Например, если провод состоит из 7 алюминиевых жил, подобных рассмотренной выше, то и сопротивление уменьшится в 7 раз, волна поджига будет бежать приблизительно в 7 раз быстрее. Если лампы меньшей мощности, то их сопротивление выше и, кроме того, тепловая инерция нити меньше.

Вы ходите в кино? Тогда вы, возможно, замечали. Герой входит в темную комнату и включает ночничок. В жизни маловаттная лампочка ночничка вспыхивает практически мгновенно. В кино же освещенность комнаты от ночничка разгорается явно замедленно. Это потому, что где-то вне поля зрения в этот момент включается более инерционный "Юпитер". Его свет и должен играть роль света ночничка, такова специфика кино.

Простенькая и эффектная модель бегущей волны поджига может получиться из лампочек для карманного фонарика. Подбирая сопротивления 2r, имитирующие сопротивления проводов, можно добиться, что десятая от источника лампа будет зажигаться на 1-2 с позже первой. Можно ли пустить это в дело?

Во-первых, это любопытная елочная игрушка. Во-вторых, это реле времени. Если настроить каскад фототранзистора так, чтобы он срабатывал при уровне яркости ВВ (рис. 57, б), то к его выходу можно подключить прибор, которому нужно почему-либо срабатывать с задержкой (например, фотоаппарат при некоторых специальных съемках). Передвинув фототранзистор к лампе 0, мы получим задержку t₀ (относительно момента включения напряжения), к лампе 1 - задержку t₁ и т. д. Мы не претендуем на изобретение нового реле времени: хотя у него и есть новизна, но второй признак изобретения - полезность - здесь может быть оспорен, так как есть более простые и точные способы решения той же задачи.

Но где-то этот эффект может оказаться полезным: ничто не должно ускользать из поля зрения изобретателя.