75. Тень столба

А Столб высотой h = 5 м и толщиной b = 10 см отбрасывает на равнину длинную тень: Солнце уже клонится к закату, высота его над горизонтом всего лишь φ = 10°. Чему равна длина тени столба? Какова будет ее длина, если высоту столба увеличить вдвое?

Б Тот, кто подходит к задаче невнимательно, решает задачу в два счета: он рисует чертеж, подобный рис. 99, затем вычисляет:

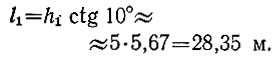
Для второго столба длина тени

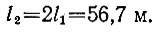
Внимательный же читатель заметит, что в таком решении никак не использована одна величина, приводимая в исходных данных, а именно толщина столба. При чем тут толщина столба? Какое отношение она имеет к длине тени? Читатель, поставивший эти вопросы, уже близок к правильному решению задачи.

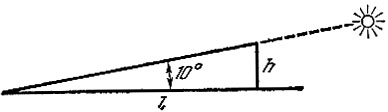
Рис. 99

Если бы тени предметов зависели не от 
величины сих последних, а имели бы свой 
произвольный рост, то, может быть, 
вскоре не осталось бы на всем земном 
шаре ни одного светлого места.

Козьма Прутков "Мысли и афоризмы", № 29.

В Приведенный выше способ вычисления длины тени верен М только в случае, когда угловые размеры источника света ничтожны малы ("точечный" источник). Солнце - далеко не точка. Его угловые размеры а равны приблизительно 0,5°. Тень в данной точке возможна только при условии, что для этой точки источник света закрыт полностью. В данном случае источник света закрывается сравнительно тонким столбом. Поэтому вполне вероятно, что в том месте, где при расчете по приведенным выше формулам должна находиться тень вершины столба, на самом деле будет всего лишь полутень, бледная, еле заметная, а то и совсем незаметная. Полная тень будет только в тех точках, для которых видимые угловые размеры толщины столба α₂ превосходят угловые размеры α Солнца С, т. е. α₂ >> а = 0,5°.

Отрезок b = 10 см виден под углом α (рис. 100) с расстояния r₁, которое можно найти из приближенной формулы

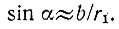
Рис. 100

Угол α₂ будет равен углу α, если

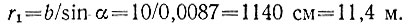
На рис. 101 показан столб ВО высотой h, его тень A₁О длиной l₁ и полутень АА₁. Длину тени, очевидно, можно найти из треугольника A₁B₁O, у которого гипотенуза равна вычисленному r₁:

Рис. 101

В вычислениях длины тени второго, более высокого столба, очевидно, нет необходимости. При данной толщине столбов длина тени не зависит от их высоты, если высота превосходит некоторую критическую, равную в нашем случае

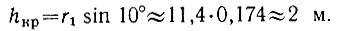
И только если h < h_кр = 2 м, то длина тени пропорциональна высоте столба.