93. Пополам не делится

А Пустотелый шар с внутренним диаметром 1 мм, абсолютно белый внутри, с абсолютно прозрачным воздухом, заполнен светом (с длиной волны λ = 0,555 мкм) так, что освещенность внутри равна 0,2 лк (такую освещенность создает полная Луна). Сколько квантов надо убрать, чтобы освещенность внутри шара упала вдвое?

Б Конечно, нужно убрать половину всего числа квантов. Но соль не в этом, а в том, сколько именно. Надо вычислить, сколько их там всего, и разделить пополам.

Напомним данные, необходимые для расчета. Один люкс - это один люмен на квадратный метр. Один ватт лучистой энергии на волне 0,555 мкм равен 683 лм светового потока. Энергия ε одного кванта равна произведению частоты у на постоянную Планка h,

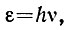
где

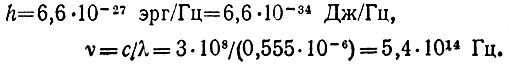
В Итак надо определить число квантов внутри шара. Энергия одного кванта

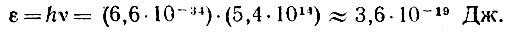
Освещенность в один люкс свяжем с джоулями:

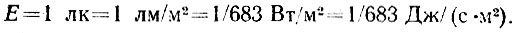
Эта освещенность дает n квантов в секунду на квадратный метр,

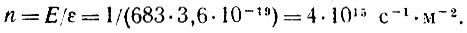
При E₁ = 0,2 лк

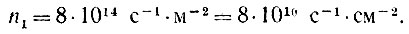
Теперь подойдем к задаче с другого конца.

В абсолютно белом шаре поглощение отсутствует, все кванты отражаются. Найдем, сколько раз в секунду отразится внутри нашего шара один квант, если он бегает вдоль диаметра шара. Для этого скорость кванта следует разделить на этот диаметр:

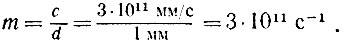
Если учесть, что в случае матовой поверхности квант отражается в самых произвольных направлениях, то число отражений будет еще больше: всякая хорда короче диаметра, время пролета по хорде меньше, чем по диаметру. Следовательно, вычисленное нами m - это минимально возможное число ударов кванта в секунду о внутреннюю поверхность шара. Чтобы не осложнять себе расчетов, удовлетворимся этим числом, памятуя, что на самом деле оно несколько больше.

Сколько же раз в секунду наш одиночный квант падает на, квадратный сантиметр поверхности?

Внутренняя поверхность шара равна

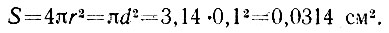
Искомое число

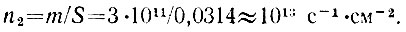
Сравнив n₂ и n₁ мы обнаруживаем, что

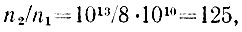
т. е. квант попадает каждую секунду на каждый квадратный сантиметр поверхности в 125 раз чаще, чем это требуется для создания освещенности в 0,2 лк. Значит, один квант внутри нашего шара создаст освещенность в 125 раз большую, чем полная Луна! 25 лк! Причем не на мгновение, не на час, а на вечность. Это как раз та освещенность, при которой мы обычно читаем книгу вечером за письменным столом.

Этот результат настолько неожидан, что хочется еще раз проверить расчеты: уж не ошиблись ли мы? И автор несколько раз это делал, но так и не нашел ошибки (в расчете!). Поэтому он вынужден смириться с этим парадоксом, но вас к этому ле принуждает. Считайте сами!

Оставляя вопрос о том, можно ли читать с помощью одного-единственного кванта, на будущее, вернемся к условию задачи.

Итак, для того чтобы внутри шара освещенность равнялась 0,2 лк, нужно, чтобы там было всего лишь ¹/₁₂₅ кванта. Но квант может быть только целым. Значит, такая освещенность невозможна! Тем более невозможно уменьшить ее вдвое. Выходит, что освещенность внутри шара может быть либо нуль (полная темнота), либо 25 лк (один квант), либо 50 л к (два кванта) и т. д. Промежуточные градации невозможны. Причем при освещенности 25 лк свет в шаре может быть только цветным (в нашем случае желтым), но не белым: белый свет представляет собой смесь многих цветов и требует для своего создания по крайней мере трех разноцветных квантов, что даст освещенность больше 25 лк.

Поистине прав Прутков, воскликнувший однажды: "Глядя на мир, нельзя не удивляться

Ты хочешь провести вечер в обществе привлекательной спутницы? В Пермском регионе есть множество красивых представительниц прекрасного пола. Посмотри на https://perm.indigram.info - и выбери свою идеальную встречу.