105. Олимпийские правила

А Кубок по футболу разыгрывается по олимпийской системе: ничьих не бывает, к следующему туру допускается только победившая команда, проигравшая же выбывает из розыгрыша. Для завоевания кубка команда должна победить во всех турах.

На участие в розыгрыше кубка поданы заявки от 16 389 команд. "Сколько матчей будет сыграно, пока определится обладатель кубка? (Не путать число матчей с числом туров!)

Б - Сейчас подсчитаем! - охотно говорят любители футбола и затем, как правило, начинают строить график розыгрыша (рис. 154), отмечая точками матчи, подводя к ним снизу по две линии, изображающие команды-участницы, и отводят от них вверх по одной, изображающей команду-победительницу.

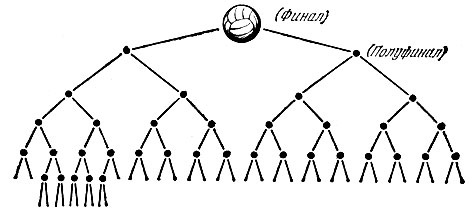
Рис. 154

- Итак, должна победить одна команда. Следовательно, в финальном матче играют две команды (один матч), в полуфинальных - четыре (два матча), четвертьфинальных - восемь (четыре матча) и т. д.

Быстро убедившись, что график довести до конца не удастся, переходят к заменяющей его таблице. Удваиваются и удваиваются Цифры, заполняются колонки, и, наконец, обнаруживается, что если бы число заявок было на пять меньше (16 384), то таблица была бы очень изящной (в двоичной системе счисления число 16 384 =2¹⁴ оказывается круглым: 100 000 000 000 000). Но деваться от пяти "лишних" команд некуда: никто не хочет считать себя лишним. Придется бросить жребий: какие-то десять команд должны пройти еще одну ступень борьбы (см. самый нижний этаж рисунка), сыграть матчи между собой и этим уменьшить число оставшихся команд на пять и добавить самую нижнюю строку в таблицу.

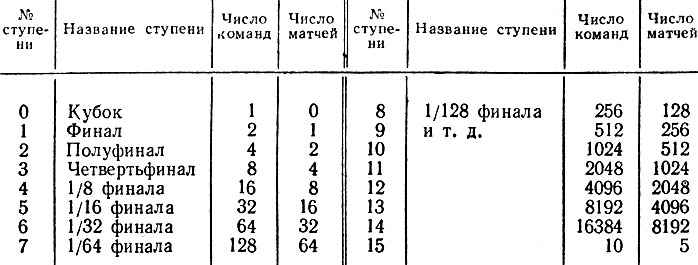
- Ну, вот, самое трудное позади. Теперь остается сложить все цифры в колонке "Число матчей" - и ответ готов!

Правильно, конечно, но уж больно длинно. Нельзя ли найти ответ без таблицы и без сложных расчетов? Одним^махом! А?

В Ответ прост: число всех матчей равно числу заявок минус единица! Надо считать не те команды, которые побеждают, а те, которые выбывают. После каждого матча выбывает одна команда: в этом, собственно, и состоит назначение каждого матча. Следовательно, надо сыграть 16 389 - 1 = 16 388 матчей, чтобы осталась одна команда-победительница. Вот и все!

Конечно, не следует умалять и роли графика и таблицы. Они позволяют ответить на многие другие интересные вопросы. Так, из таблицы видно, что для завоевания кубка нужно выиграть не так уж много матчей, как это могло показаться вначале,- всего лишь 15 (и то это относится только к тем десяти командам, жребий которых оказался менее счастливым; остальным же достаточно победить 14 раз). Из графика видно даже, кому с кем предстоит встречаться на каждой ступени... если на нее удастся взобраться. Все это полезно и интересно, но все это лишнее в рамках поставленной задачи.