Глава двенадцатая. Расширение понятия времени

"Все существенные идеи в науке 
родились в драматическом конфликте 
между реальностью и нашими попытками ее понять".

А. Эйнштейн и Л. Инфельд

Время в классической механике

Всегда ли, в любых ли условиях темп течения времени одинаков?

Если мимо вас с большой скоростью проносятся часы, то можно ли быть уверенным в том, что их показания точно соответствуют показаниям ваших часов?

Когда какое-нибудь радиоактивное вещество движется с большой скоростью относительно земной поверхности, а вы, находясь на земной поверхности, определяете скорость его распада, то можно ли поручиться за то, что результат этих измерений совпадет с данными, полученными в обычных условиях, т. е. тогда, когда точно такой же радиоактивный препарат лежит неподвижно в банке, стоящей на вашем столе?

Если пароход плывет вдоль берега со скоростью 15 км/час, а пассажир идет по его палубе от кормы к носу, т. е. в направлении его движения, со скоростью 5 км/час, то скорость его движения относительно берега равна 20 км/час. Если он идет с той же скоростью против движения парохода, то его скорость относительно берега 10 км/час. А если в аналогичном опыте все скорости увеличить в миллионы раз, то останется ли справедливым этот закон сложения скоростей?

С точки зрения "здравого смысла", основанного на обыденном житейском опыте, на все эти вопросы нужно ответить: да. То же самое нужно было бы сделать и на основе классической механики, построенной до XX века трудами Галилея, Ньютона и ряда других ученых. Более того, с точки зрения этой науки все эти вопросы странные, если не вздорные.

В своих "Математических началах натуральной философии" Ньютон писал:

"Абсолютное, истинное и математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью".

"Относительное, кажущееся или обыденное время есть или точная или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как-то: час, день, месяц, год".

"Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается везде одинаковым и неподвижным".

"Абсолютное время не может быть изменено в своем течении. Одна и та же продолжительность и одно и то же состояние соответствуют существованию всех вещей, безразлично, скоры ли движения, медленны или равны нулю".

Таким образом, по Ньютону возможно движение относительно пространства, а темп течения времени не зависит от характера и скорости движения тел. К этому остается еще добавить, что частью классической механики является закон сложения скоростей при переносном движении, предложенный Галилеем и имеющий вид: w = v₁+v₂. По этому закону результирующая скорость w равна сумме составляющих скоростей v₁ и v₂, взятых с учетом их направлений. Если обе составляющие скорости направлены в одну и ту же сторону, то результирующая равна их сумме, если в разные - разности.

В XVII-XIX веках один успех классической механики следовал за другим. На ее основе были вычислены орбиты планет. Некоторое время спустя обнаружились уклонения реальных орбит от вычисленных. Поставило ли это под сомнение формулы классической механики? Напротив. Случилось так, что указанные уклонения реальных орбит от вычисленных лишь с еще большей убедительностью продемонстрировали правильность уравнений классической механики.

Эти научные события произошли следующим образом. Исходя из предположения о том, что уклонение реальной орбиты планеты , Уран от вычисленной обязано притяжению другой, более далекой и пока еще не известной планеты нашей солнечной системы, Джон Адаме к 1845 г. вычислил орбиту новой планеты и указал ее положение на небесном своде. Теперь мы знаем, что он это сделал с погрешностью, меньшей 2°. Между тем Урбан Леверье, не зная о расчетах Адамса и совершенно независимо от него, сделал такие же расчеты и закончил их к 1846 г. Леверье послал письмо астроному Иоганну Галле с указанием места на небосводе, в котором нужно искать новую планету. По получении письма тот в тот же вечер и вблизи от указанного места обнаружил новую планету, которая получила название Нептун.

Перечисление целого ряда блестящих успехов, достигнутых на основе классической механики, можно было бы продолжить.

Между тем представления о времени и пространстве, лежащие в основе классической механики, неоднократно подвергались критике. Иные взгляды высказывались и до Ньютона, и после него. Однако до тех пор, пока классическая механика успешно решала научные задачи, твердо держались и ее основы.

Некоторые трудности классической механики

В конце XIX века ученых очень занимали вопросы о распространении света и о скорости "эфирного ветра". Напомним, что в те времена предполагалось, что электромагнитные колебания распространяются в эфире - некоей тончайшей среде, заполняющей все пространство. Полагая этот эфир неподвижным, ученые считали, что различные тела, двигаясь сквозь него, встречают эфирный ветер. Ставя задачу об определении скорости эфирного ветра, ученые хотели таким образом определить абсолютную скорость движения Земли.

Идея соответствующего эксперимента была сформулирована еще Максвеллом, который писал; "Если бы можно было измерить скорость света по времени, которое ему требуется, чтобы пройти расстояние между двумя точками на поверхности Земли, а потом полученные данные сравнить со скоростью света в обратном направлении, то мы смогли бы определить скорость движения эфира относительно этих двух точек".

Легко видеть, что идея этого опыта очень проста, почти очевидна и основана на законе сложения скоростей Галилея. В самом деле, если этот закон справедлив (а в этом в XIX веке никто не сомневался) и Земля движется относительно эфира, то такой опыт должен был позволить вполне однозначно определить скорость этого движения.

Однако в техническом отношении такой опыт совсем не прост. Скорость света в вакууме с = 300 000 км/сек, а скорость орбитального движения Земли v = 30 км/сек. Отношение этих скоростей равно ^v/_c = 10^-4, а квадрат этого отношения составляет лишь v²/c²=10^-8. Между тем ряд соображений привел ученых к тому, что для определения абсолютного движения Земли годятся лишь методы, основанные на измерении v²/c².

Довольно долгое время ученым не удавалось построить пригодные для этого приборы. Лишь в конце XIX века Альберт Майкельсон разработал и построил свой интерферометр - прибор, обладающий очень высокой чувствительностью и точностью. В этом приборе луч света от какого-либо источника с помощью полупрозрачного зеркала разделяется на два пучка. Эти пучки света некоторые отрезки пути проходят во взаимно перпендикулярных направлениях, а затем сходятся в одном и том же месте на экране прибора. При этом на экране возникает интерференционная картина. Если источник света монохроматический, то интерференционная картина представляет собой чередование светлых и темных полос. Когда длительность распространения света в одном из пучков почему-либо изменяется, то происходит сдвиг этих полос. Такой прибор позволяет обнаружить даже крайне небольшое запаздывание распространения одной из электромагнитных волн по отношению к другой. В конце XIX века этот прибор был шедевром тонкой измерительной техники.

Располагая прибор так, что один из лучей света двигался в нем по направлению движения Земли, а другой перпендикулярно к этому направлению, Майкельсон предполагал таким образом обнаружить движение Земли относительно эфира и измерить скорость этого движения. В 1881 г. Майкельсон опубликовал свои первые результаты, а в 1888 г. - результаты повторных и более точных измерений, проделанных совместно с Эдвардом Морли. Оба исследования показали, что скорость света одинакова при распространении его в любом направлении: по движению Земли, против него и перпендикулярно к нему. Таким образом, из этих опытов следовало, что скорость распространения света постоянна. Причем постоянна не для неподвижного эфира, а для движущейся Земли.

Как понять этот экспериментальный факт? Почему закон сложения скоростей классической механики; который неоднократно проверялся и до сих пор всегда оправдывался, в случае света, Земли и эфира нарушается? По этому вопросу в конце XIX и начале XX века происходили острые дискуссии.

К тому времени уже накопилось много данных, свидетельствовавших о том, что свойства эфира - странные и во многом противоречивые. В самом деле, световые волны распространяются с большой скоростью и на огромные расстояния. Между тем в любом из известных на Земле материалов Скорость распространения колебаний тем больше, а происходящие при этом потери энергии тем меньше, чем больше упругость этого материала. Таким образом, если носителем световых волн является эфир, то его упругость должна быть колоссальной. Однако космические тела движутся в этом эфире, не встречая сколько-нибудь заметного сопротивления. Следовательно, эфир должен быть абсолютно проницаемым. Не просто согласовать эти два положения, не правда ли?

Эрнст Мах предложил вообще отказаться от эфира, Оливер Лодж рекомендовал сохранить его. Джордж Фитцджеральд объяснил отрицательный (в смысле обнаружения абсолютного движения) результат опыта Майкельсона тем, что при движении тел их размеры в направлении движения уменьшаются, и как раз на столько, чтобы компенсировать изменение скорости света.

На первый взгляд предложение Фитцджеральда может показаться слишком фантастичным. Однако в самом конце XIX века Гендрик Лорентц построил теорию электрона, из которой следовало, что при движении он сжимается в направлении перемещения, и притом тем больше, чем больше его скорость. Далее он предположил, что так же ведут себя и все тела. В 1895 г. он писал: "Как ни странна на первый взгляд указанная гипотеза, нужно будет все же признать, что она вовсе не так неприемлема, если только мы допустим, что и молекулярные силы передаются через эфир, подобно тому как мы можем теперь определенно утверждать это относительно электрических и магнитных сил. Если это так, то весьма вероятно, что поступательное движение изменит взаимодействие между двумя молекулами или атомами подобным же образом, как и притяжение или отталкивание между заряженными частицами. Так как форма и размеры твердого тела в конечном итоге обусловливаются интенсивностью молекулярных взаимодействий, то в этом случае не может не произойти и изменение размеров". И далее: "Перемещение ... обусловило бы сокращение в направлении движения в отношении 1:√1-v²/c²"

Гипотеза Лорентца и следующий из нее вывод о сокращении тел в направлении их движения поворачивают всю задачу неожиданно и необычно. Получается, что хотя эффект есть, но с помощью опыта Майкельсона обнаружить его нельзя. В самом деле, ведь в приборе Майкельсона распространение света происходит между определенными точками, расстояние между которыми составляет базу прибора, Нетрудно понять, что изменение длительности распространения света от одного конца базы прибора до другого может произойти по крайней мере по двум причинам: из-за изменения скорости движения световой волны и в результате изменения длины этой базы. Так вот, по гипотезе Лорентца получается так, что при движении Земли и расположенного на ней прибора Майкельсона база этого прибора укорачивается как раз на столько, что это компенсирует изменение oскорости света.

Итак, Лорентц высказал два предложения. Первое заключается в том, что при движении тел происходит изменение их размеров, массы, а также темпа течения времени. При этом он дал группу формул (получивших название преобразований Лорентца), представляющих количественное выражение сокращения длины, увеличения массы и замедления темпа времени в зависимости от скорости движения тел.

Второе предложение Лорентца заключается в объяснении отрицательного (в смысле обнаружения абсолютного движения Земли) результата опыта Майкельсона. В этом объяснении сохранены законы классической механики и светоносный эфир, отнюдь не отрицается абсолютное движение и в то же время с необычным остроумием показано, почему в опыте Майкельсона обнаружить это абсолютное движение не удается. Однако многие ученые посчитали такое объяснение необоснованным. Как известно, время-лучший судья во многих спорах. Преобразования Лорентца вошли в основной фонд науки, гипотеза об изменении молекулярных сил при движении отпала. Однако для того, чтобы это произошло, понадобились новые факты и новые идеи.

Время в специальной теории относительности

В начале XX века трудности классической механики, связанные с отрицательным результатом опыта Майкельсона, еще не были преодолены. Между тем к ним добавились еще и другие, так как еще в нескольких опытах с телами, движущимися с очень большой скоростью, обнаружились отклонения от законов классической механики.

В 1905-1908 гг. Альберт Эйнштейн разработал и опубликовал специальную теорию относительности, в которой дал совершенно неожиданное, очень изящное и кардинальное решение всей проблемы. При этом оказалось необходимым существенно расширить существовавшие в XIX веке понятия о времени, размерах и массе тел.

Для того чтобы суть этих новых идей предстала более, наглядно, рассмотрим на ряде примеров несколько аспектов классической механики. Для начала воспользуемся примером очень простым: пусть в движущемся поезде яблоко падает с полки на пол вагона. Какой будет траектория падения яблока с точки зрения пассажира, находящегося в вагоне? Какой будет траектория падения этого же яблока с точки зренля наблюдателя, стоящего на железнодорожной платформе, мимо которой проходит поезд?

Ответ оказывается простым лишь при определенных условиях, и мы их сейчас, оговорим. Поезд может двигаться ускоренно,, замедленно, или равномерно. Он может идти по кривой и по прямой. Выберем наиболее простые условия: пусть поезд движется без каких-либо толчков, совершенно равномерно и прямолинейно. Для удобства дальнейших рассуждений введем две прямоугольные системы, координат. Одну из них назовем № 1 и мысленно свяжем ее с железнодорожной платформой. Расположим ее так, чтобы ось х лежала в горизонтальной плоскости и была ориентирована по направлению железнодорожного пути, ось у лежала в той же горизонтальной плоскости и была направлена перпендикулярно к оси х, а ось z была расположена перпендикулярно к ним обеим, т. е. вертикально. Другую систему координат назовем № 2, мысленно свяжем ее с движущимся поездом и в ней ось х совместим с осью поезда, ось у расположим в горизонтальной плоскости перпендикулярно к оси х, а ось z направим по вертикали. Это обычная процедура, которую выполняют физики, изучая какие-либо процессы.

Наблюдатель, стоящий на платформе, считает себя неподвижным. Так ли это? Ведь он перемещается вместе с Землей, а движение Земли относительно звезд непрямолинейное, неравномерное и достаточно сложное. Однако для простоты и удобства дальнейших расчетов посчитаем, что система № 1, с которой связан наблюдатель на платформе, и система № 2, с которой связан пассажир в поезде, движутся равномерно и прямолинейно, но с различной скоростью. В этом утверждении содержится определенное упрощение задачи, однако в данном случае вполне допустимое.

В общем, при решении довольно многих физических задач оказывается удобным и допустимым вводить различные упрощения. Такой метод не вызывает возражений, если только эти упрощения делаются достаточно обоснованно. Например, при расчете траектории движения Земли вокруг Солнца можно не учитывать собственные размеры Земли, так как они намного меньше расстояния между Солнцем и Землей. При изучении процессов, происходящих в движущихся системах, в ряде случаев можно считать, что эти системы движутся с постоянной, хотя и различной скоростью. Даже нашу Землю с ее неравномерным, криволинейным и сложным, движением можно посчитать системой, движущейся равномерно и прямолинейно, если только изучается процесс достаточно кратковременный и поэтому весь он разыгрывается - начинается, протекает и заканчивается - на очень небольшом отрезке траектории движения Земли.

Напомним, что для того, чтобы какое-либо тело изменило направление или скорость своего движения, нужно, чтобы на него действовала внешняя сила. Напротив, если внешние силы на тело не действуют, то оно движется равномерно и прямолинейно. Свяжем с каждым из тел систему отсчета. Можно представить себе существование целого ряда таких систем, движущихся равномерно друг относительно друга. Их принято называть инерциальными системами.

Классическая механика утверждает - и это подтверждено знаниями, добытыми в течение многовекового развития науки,- что все физические законы одинаково справедливы для любой инерциальной системы.

Теперь вернемся к нашей задаче с яблоком. Наблюдатель, находящийся в вагоне и описывающий явления с помощью системы координат № 2, связанной с поездом, отметит, что яблоко падает вертикально. Воспользовавшись часами и масштабной линейкой, он может установить также, что при падении яблоко движется ускоренно, точно следуя закону падения тел под действием силы тяжести.

Наблюдатель, находящийся на платформе, пользуясь своей системой координат №1, связанной с железнодорожными рельсами, увидит нечто другое. Если стенки движущегося мимо него вагона сделаны из прозрачной пластмассы, то, засняв киноаппаратом падение яблока, он отметит, что яблоко двигалось не вертикально, а по наклонной кривой. Для описания этого движения наблюдателю на платформе, пользующемуся своей системой координат №1, понадобятся несколько более сложные формулы, чем наблюдателю в вагоне.

Пусть, для определенности, наш наблюдатель на платформе является физиком, живущим в конце XIX века. Тогда в этой задаче для него нет ничего сложного, так как он знает уравнение движения тел при свободном падении и формулы преобразования для перехода от одной инерциальной системы к другой. Он отдает себе отчет в том, что в опыте, продолжающемся доли секунды, и Землю и поезд можно посчитать инерциальными системами, и ему хорошо известно, что для того, чтобы определить скорость движения яблока относительно его системы №1, нужно скорость движения яблока в системе № 2 сложить геометрически (т. е. с учетом направления движения) с относительной скоростью движения этих инерциальных систем друг относительно друга. При этом он твердо уверен в том, что длина масштабных линеек, масса яблока и ход часов (т. е. темп течения времени) не зависят от того, из какой системы - №1 или №2 - они определяются и какова относительная скорость движения этих систем.

Рассмотрим теперь несколько более сложный пример. От глубокой древности и в течение многих веков астрономы изучали движение планет и Солнца. При этом они определяли и вычерчивали очень сложные траектории их перемещений относительно звезд, в которых прямое движение планет время от времени перемежается остановками и сменяется возвратным движением. Так как астрономы древнего мира и средних веков считали Землю неподвижной - центром мира, то они, естественно, пользовались системой координат, связанной с Землей. Для того чтобы объяснить сложные и причудливые движения планет, Клавдием Птоломеем (II век н. э.) и другими астрономами, так же как и он решавшими эту задачу в координатной системе, связанной с Землей, была придумана система эпициклов, т. е. ряда одновременных и совместных вращательных движений планет. Эта система была очень сложной, но довольно точно описывала видимые движения планет и для того времени, конечно, была большим научным достижением. Например, объяснение траектории движения Юпитера заключалось в круговом движении этой планеты по эпициклу - окружности, центр которой в свою очередь движется по другой окружности, в центре которой находится Земля, и т. д.

Много веков спустя Николай Коперник (1473 - 1543 гг.) рассмотрел эти же движения в координатной системе, связанной с Солнцем, и они приобрели простоту и стройность. Проделав такое преобразование координат, Коперник, как известно, пошел и дальше, высказав утверждение, что все планеты, в том числе и Земля, на самом деле вращаются вокруг Солнца. Эта работа Коперника справедливо считается одним из крупнейших достижений науки.

В середине XIX века законы классической механики и очень точные астрономические наблюдения позволили глубоко изучить движения известных планет и по небольшим отклонениям реальных их движений от расчетных предсказать существование неизвестных в то время далеких планет. Тем не менее при анализе планетных движений на основе классической механики обнаружилась и некая червоточинка: в траектории движения Меркурия - планеты, наиболее близкой к Солнцу и поэтому вращающейся вокруг него быстрее всех других планет,- было замечено такое уклонение реальной траектории от расчетной, которое на основе классической механики объяснить не удалось. К этому обстоятельству мы еще вернемся.

Итак, из этих примеров можно видеть, что важной составной частью классической механики, наряду с законами природы, являются законы преобразования координат. Напомним еще раз, что в том случае, когда процессы, происходящие в одной инерциальной системе, почему-либо приходится описывать и рассчитывать с помощью системы координат, связанной с другой инерциальной системой, применяющиеся при этом законы преобразования классической механики учитывают изменение координат и скоростей, но оставляют неизменными темп течения времени, а также размеры и массу тел.

Таким образом, ситуация, с которой в начале XX века столкнулся Эйнштейн, заключалась в том, что считались твердо установленными следующие положения:

1. Законы природы одинаково справедливы для любой инерциальной системы.

2. При переходе от одной инерциальной системы к другой справедливы законы преобразования координат классической механики.

3. Скорость света в вакууме постоянна и не зависит от скорости движения источника и наблюдателя.

К этому нужно еще добавить, что физики XIX века считали, что распространение света происходит через эфир - некую тонкую среду, проникающую через все тела.

Как мы уже знаем, особенность этой ситуации заключается в том, что эти положения между собой не совместимы, а свойства эфира противоречивы. В самом деле, если законы природы одинаково справедливы для любой инерциальной системы и при этом действуют законы преобразования классической механики для перехода от одной из них к другой, то скорость света должна зависеть от направления и скорости движения системы. Между тем на самом деле она в любой системе постоянна.

Если эфир увлекается телами при их перемещении, то при движении источника света к наблюдателю или от него наблюдатель должен был бы обнаружить изменение скорости света. Если при движении тел эфир совершенно не увлекается ими, если все тела перемещаются в абсолютно неподвижном эфирном море, то наблюдатель, движущийся относительно этого эфирного моря в разных направлениях и с разной скоростью, каждый раз обнаруживал бы, что свет имеет разную скорость, и, таким образом, мог бы установить свое абсолютное движение. Как известно, скорость света постоянна в любых случаях, и поэтому гипотезу о светоносном эфире, как явно противоречивую, нужно отбросить.

Однако это еще не спасает дела. Кроме этого нужно еще отказаться по крайней мере от одного из трех указанных выше положений. Эйнштейн в качестве основания для своей специальной теории относительности выбрал первое и третье утверждения, т. е. положение о постоянстве скорости света (экспериментальный факт!) и положение об одинаковой применимости законов природы для любой инерциальной системы (универсальность законов природы!), и отказался от второго, т. е. от законов преобразования классической механики.

Разумеется, отказавшись от них, он должен был предложить другие. Это и было им сделано. Преобразования координат теории относительности основаны на новом подходе к метрике мира. В основе этого нового подхода лежит анализ реальной процедуры измерений. Проводя этот анализ, Эйнштейн показал, что состояние физического тела характеризуется четырьмя координатами: тремя пространственными и одной временной, которые, в отличие от классической механики, не обособлены друг от друга, а взаимосвязаны. С помощью ряда мысленных опытов, представляющих анализ реальной ситуации измерений, Эйнштейн установил, что, находясь в одной инерциальной системе и наблюдая события или процессы, происходящие в другой, которая движется относительно первой с постоянной скоростью, наблюдатель обнаруживает в другой системе замедление темпа течения времени, уменьшение размеров тел и увеличение их массы, причем в количественном отношении это происходит в соответствии с формулами преобразований Лорентца.

Для интервала времени соответствующая формула преобразования имеет вид

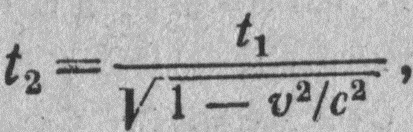
где t₁ - интервал времени между двумя какими-либо событиями, происходящими в первой инерциальной системе, измеряемый с помощью часов, находящихся в этой же первой системе, t₂ - интервал времени между теми же двумя событиями, происходящими в первой инерциальной системе, отмечаемый с помощью часов, находящихся во второй инерциальной системе, с - скорость света в вакууме, v - относительная скорость движения первой и второй инерциальных систем.

Когда скорость относительного движения инерциальных систем достаточно большая, например составляет 150000 км/сек, т. е. половину скорости света, то v²/c² = 1/4, a √l - v²/с² = 0,866. Нетрудно подсчитать, что при такой скорости движения наблюдатель, измеряющий скорость процессов, происходящих в системе № 1, из своей системы № 2, отметит, что они протекают на 17% медленнее, чем аналогичные процессы в его системе. Нетрудно увидеть также, что в том случае, когда скорость относительного движения инерциальных систем очень мала (vc), то величина отношения v²/c² близка к нулю, соответственно член √1 - v²/c² близок к единице, а вся формула преобразования приобретает вид: t₂=t₁. Между тем это выражение есть не что иное, как формула преобразования классической механики, по которой темп времени в разных инерциальных системах одинаков.

В классической механике молчаливо подразумевалась мгновенная передача сигналов с бесконечной скоростью, и поэтому можно было говорить об одновременности событий в любой точке Вселенной и для тел, движущихся с любой скоростью. В теории относительности принимается во внимание, что скорость света в вакууме является наивысшей скоростью для распространения сигналов и в этом смысле является предельной. Между тем, если сигналы распространяются с конечной скоростью, а наблюдаемые тела и наблюдатели находятся в разных местах и движутся с разной скоростью, то события, одновременные для одного наблюдателя, в общем случае уже не являются одновременными для другого.

Далее Эйнштейн показал, что в теории относительности сложение скоростей двух тел описывается уже не законом Галилея, а несколько более сложным выражением, причем так, что суммарная скорость всегда меньше арифметической суммы слагающих скоростей и никогда не может превысить предельной, т. е. скорости света в вакууме.

Существенно отметить, что в том предельном случае, когда относительная скорость движения инерциальных систем очень мала, все формулы преобразования теории относительности переходят в формулы преобразования классической механики. Таким образом, теория относительности включает в себя классическую механику как некий частный случай, имеющий место при малых скоростях движения инерциальных систем.

Резонно поставить вопрос: какую скорость в теории относительности следует считать большой и какую малой? В теории относительности большой является скорость, сравнимая по величине со скоростью света, а скорость пули или самолета оказывается малой. В самом деле, даже если скорость современного сверхзвукового реактивного самолета посчитать равной 3600 км/час или 1 км/сек, то отношение v²/с²=1,1*10^-11. При этом характерный член, входящий в формулы преобразования теории относительности, √1 - v²/c², отличается от единицы лишь на 5,5*10^-12. Поэтому с точки зрения земного наблюдателя при полете такого самолета время для пилота течет медленнее, чем для людей, находящихся на Земле, однако лишь на 5 десятимиллиардных долей процента. С точки зрения земного наблюдателя в таком же отношении изменяются размеры и массы при полете этого самолета, а также всех находящихся на нем тел. Между тем при измерении длины или массы столь малые величины пока еще лежат за пределами, доступными современной измерительной технике.

Возможны и такие вопросы: насколько реальны различия между выводами, получаемыми с помощью теории относительности и классической механики, сколь эти различия велики и имеют ли они практическое значение?

Мы уже упоминали, что астрономы обнаружили различие между реальной траекторией движения планеты Меркурий и рассчитанной на основе классической механики. Это различие было отмечено в положении оси эллипса, по которому Меркурий движется вокруг Солнца. Оказалось, что оно составляет 42 угловые секунды за 100 лет. Неправда ли, не так уже много? Но то, что это различие есть, а объяснить его не удается, подрывало

классическую механику и в XIX веке мучило многих ученых. Между тем с помощью теории относительности удалось объяснить это различие и получить расчетную траекторию Меркурия, совпадающую с реальной. Для строгости изложения отметим, что вначале, на основе специальной теории относительности, удалось объяснить лишь часть этого различия, а в дальнейшем, на основе общей теории относительности, это различие удалось объяснить полностью.

При Движениях, скорость которых близка к скорости света, теория относительности дает результаты, существенно отличающиеся от получаемых на основании классической механики. В современной ядерной технике, при изучении частиц больших энергий, при проектировании и работе различных ядерных устройств,- оказывается совершенно необходимым это учитывать. В самом деле, ведь в ряде таких устройств приходится сталкиваться с тем, что темп течения времени у частиц, движущихся в этих приборах, а также размеры и масса этих частиц изменяются на десятки и сотни процентов. Если это не принимать во внимание, то такие приборы - циклотроны, синхротроны и т. д.- попросту не будут работать.

Далее подробно рассмотрен один важный и интересный пример такого рода. Однако прежде чем перейти к его изложению, нужно сделать одно замечание, причем не столько физического, сколько исторического и психологического характера.

В основе специальной теории относительности лежит положение о постоянстве скорости распространения света, и экспериментально этот факт был обнаружен Май-кельсоном несколько раньше, чем Эйнштейн опубликовал свои первые статьи по теории относительности. Во многих книгах создание специальной теории относительности описывается так, будто именно открытие Майкельсоном постоянства скорости распространения света и привело Эйнштейна к его новым идеям. Действительно, излагать теорию относительности удобнее, если посчитать, что новый экспериментальный факт привел к новым теоретическим обобщениям. Так обычно в науке, и бывает, и поэтому это логично.

Между тем в данном случае было по-другому. Из ряда статей, высказываний и переписки того времени следует, что Эйнштейн формулировал свою специальную теорию относительности независимо от работ Майкельсона. Положение о постоянстве скорости распространения света Эйнштейн рассматривал как необходимое следствие из ряда явлений электродинамики, а опыт Майкельсона, с которым он был знаком,- лишь как подтверждение своих теоретических выводов.

Между тем в те же годы, т. е. в самом конце XIX и начале XX века, Майкельсон полученные им важные экспериментальные результаты о постоянстве скорости распространения света оценивал если не как ошибку, то во всяком случае как неудачу. Сейчас нам это может показаться странным, но в те годы Майкельсон считал, что скорость света обязательно должна быть различной в разных направлениях, а он попросту не смог этого обнаружить.

Таким образом, в том, что в вопросе о постоянстве скорости распространения света Эйнштейн больше опирался на свои теоретические построения, чем на экспериментальные результаты Майкельсона, со стороны Эйнштейна не было и тени желания умалить заслуги Майкельсона. Напротив, в ряде своих статей и речей он охотно и щедро воздавал ему должное. В этом было другое: огромная сила теоретической мысли и глубокая уверенность в правильности новых научных идей.

Какое драматическое стечение обстоятельств иногда преподносит жизнь, не правда ли?

Среднее время жизни мюона и его энергия

"Нестабильные мезоны можно рассматривать как субатомные "часы", 
движущиеся с очень большими скоростями. Поэтому измеренное среднее 
время жизни этих мезонов значительно больше среднего 
времени жизни мезонов, находящихся в покое". 

Б. Росси

Сколь велико изменение темпа времени в движущихся телах, насколько реален этот эффект и как его можно наблюдать? .Для ответа на эти вопросы было бы очень удобно иметь двое одинаковых часов, одни расположенные в нашей земной лаборатории, а другие проносящиеся мимо нас со скоростью, близкой к скорости света. Такая возможность есть, и ниже рассказано, как этот опыт был осуществлен.

В 1936-1938 гг. Андерсон и Неддермеер, а также Стрит и Стивенсон, исследуя космические лучи, обнаружили в них проникающее излучение, которое по ряду признаков отличалось от быстрых электронов и быстрых протонов. Проведенные ими исследования показали, что это излучение представляет собой поток быстрых положительно и отрицательно заряженных частиц, имеющих массу большую, чем у электронов, и меньшую, чем у протонов. Так были открыты новые частицы, которые получили название μ-мезонов или мюонов. По современным данным масса положительных и отрицательных мюонов одинакова и равняется приблизительно 207 электронным массам.

Вскоре обнаружились некоторые странности поведения этих частиц.

Заряженные частицы при прохождении через слои вещества теряют энергию на ионизацию и частично поглощаются. Обычно проникающую способность частиц оценивают по их поглощению в слое вещества данной плотности и толщины. Для того чтобы сразу учесть оба эти фактора, массу поглощающего слоя оценивают по числу граммов данного вещества на квадратный сантиметр площади. Оказалось, что мюоны сильнее поглощаются в воздухе, чем в эквивалентных по массе слоях свинца или латуни.

Такие опыты были повторены многими авторами. Ведь непонятное всегда влечет ученых. За ним скрывается иногда ошибка, чаще - новое открытие. Были проведены систематические исследования интенсивности мюонов на уровне моря и на разных высотах, при наличии и в отсутствие поглощающего слоя. Эти опыты подтвердили наличие аномального поглощения мюонов при прохождении их через толстые слои воздуха. Более того, ослабление интенсивности мюонов в воздухе при движении их под углом оказалось больше, чем при движении по вертикали, хотя при этом учитывалось увеличение массы воздуха, пересекаемого частицей.

Объяснение странности поведения мюонов было дано в 1938 г. Г. Куленкампфом, предположившим, что мюоны не стабильны и что среднее время их жизни того же порядка величины, что и длительность прохождения через слой атмосферы. В этом случае ослабление интенсивности потока мюонов при прохождении через слой атмосферы объясняется не только прямым их поглощением, но и самопроизвольным распадом. В то же время ослабление интенсивности мюонов при прохождении их через слой металла обязано лишь прямому поглощению, так как длина пути мюона в эквивалентном по массе слоях металла всего несколько сантиметров или дециметров и соответствующее время во много раз меньше среднего времени жизни мюона.

В дальнейшем многие исследователи подтвердили распад мюонов и показали, что он происходит по схеме в μ^±→e^±+v+~v, т. е. положительный мюон распадается на позитрон, нейтрино и антинейтрино, а отрицательный мюон - на электрон, нейтрино и антинейтрино.

В 1939 г. Б. Росси провел серию исследований для определения среднего времени жизни мюонов^*. Идея этих опытов очень проста и является развитием высказываний Г. Куленкампфа. Она заключается в следующем: так как мюоны радиоактивны, то при прохождении через слой вещества их число убывает не только вследствие поглощения, но и в результате распада. Следовательно, чем больше время пролета в слое вещества, тем больше мюонов успевает распасться. Если мюоны проходят через различные слои вещества, имеющие одинаковую массу, но различные толщину и плотность, то относительная убыль числа мюонов тем больше, чем толще слой и чем короче среднее время их жизни.

^* (Б. Росси, Космические лучи, Атомиздат, М., 1966.)

Таким образом, измерив уменьшение интенсивности мюонов в соответствующим образом подобранных слоях различных веществ (например: воздуха, воды, графита), можно определить среднее время жизни мюонов. Именно это и сделал Росси. Он провел измерения интенсивности мюонов в Чикаго (на высоте 180 м над уровнем моря), Денвере (1600 м над уровнем моря), Эхо Лейк (3240 м над уровнем моря) и на горе Эванс (4300 м над уровнем моря), т. е. в пунктах, куда мюоны попадали, пройдя слои воздуха разной толщины и плотности. В каждом из этих пунктов он проводил две серии измерений: без фильтра и с графитовым фильтром определенной толщины. Таким образом он получал также данные об ослаблении потока мюонов в тонком слое плотного вещества. Обработка результатов этих измерений показала, что среднее время жизни мюонов составляет несколько микросекунд.

В последующие годы, несколько усовершенствовав измерительную аппаратуру, Б. Росси и Д. Холл провели серию измерений среднего времени жизни движущихся мюонов, но уже не для суммарного их потока, а.для отдельных групп различной энергии. При этом оказалось, что у мюонов большой энергии, т. е. быстрых, среднее время жизни приблизительно в три раза больше, чем у мюонов малой энергии, т. е. более медленных. Как оценить этот результат?

Для измерения времени может быть использован любой процесс, периодически повторяющийся (например, качания маятника) или протекающий равномерно (например, высыпание песка, радиоактивный распад). Когда физики в своих лабораториях изучали скорость распада различных радиоактивных веществ, то они столкнулись с тем, что у одних изотопов период полураспада составляет миллиарды лет, а у других - лишь тысячные и миллионные доли секунды. При этом оказалось, что изменения температуры и давления в пределах, достижимых в земных лабораториях, не влияют на скорость распада. Таким образом, радиоактивные вещества могут служить для отсчета интервалов времени, т. е. работать как своеобразные часы и притом с большим постоянством.

С этой точки зрения мюоны, как и любые другие радиоактивные частицы, тоже могут рассматриваться как своеобразные часы. Почему же эти "часы" изменяют свои показания при изменении энергии и скорости движения частиц? Почему быстрые мюоны живут дольше медленных?

Росси и Холл объяснили это тем, что по теории относительности темп течения любого процесса в природе зависит от скорости движения системы, в которой этот процесс происходит, относительно другой системы, на которой расположены наблюдатель и его измерительные приборы. Поскольку мюоны относительно Земли движутся с очень большой скоростью, близкой к скорости света, то и эффект замедления времени достигает большой величины, порядка сотен процентов. Указанные авторы пошли еще дальше: располагая данными о среднем времени жизни движущихся мюонов. по Формулам теории относительности они вычислили, что среднее время жизни покоящихся мюонов должно составлять около двух микросекунд.

Ф. Разетти решил определить среднее время жизни покоящихся мюонов экспериментально. Так как мюон распадается на электрон или позитрон и нейтрино и антинейтрино (μ^±→e^±+v+~v), то для определения его среднего времени жизни нужно зафиксировать два события: остановку мюона и его распад, и измерить интервал времени между ними. Эта задача была решена с помощью остроумного по замыслу и виртуозного по технике эксперимента, осуществленного Разетти в 1941 г. с помощью схемы запаздывающих совпадений. По тому же принципу, но с несколько улучшенной методикой и большей точностью в 1942-1943 гг. среднее время жизни покоящегося мезона было определено Росси и Нерсоном.

Схема этих опытов следующая (рис. 48). На пути мезонов ставится несколько фильтров 1, 2, 3 и несколько групп счетчиков А, В, С, D, F. Все счетчики, помеченные одной и той же буквой, соединены между собой параллельно. Это означает, что они работают просто как один счетчик большой площади.

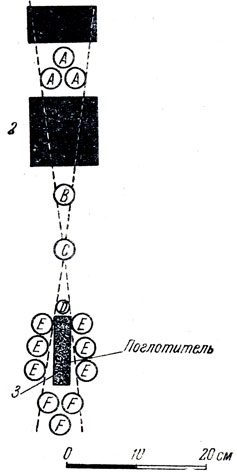
Рис. 48. Схема опыта для oпределения среднего времени жизни покоящегося мезона

Счетчики групп А, В, С, D соединены в приборе по схеме совпадений. Это означает, что прибор выдает результирующий сигнал только тогда, когда наблюдаемая частица проходит через все эти группы счетчиков. Этим самым из всего потока космических лучей вырезается узкий направленный пучок таких частиц, которые способны пройти через два толстых свинцовых фильтра 1 и 2, а это возможно лишь для частиц определенного типа и энергии. Таким образом, "ядерный телескоп" отбирает частицы нужного типа.

Третий фильтр нужен для наблюдения остановившихся мезонов. Еще одна группа счетчиков помещена за этим фильтром (группа F) и соединена в приборе со всеми остальными по схеме антисовпадений. При этом прибор выдает результирующий сигнал только тогда, когда наблюдаемая частица проходит через группы счетчиков А, В, С, D, но не проходит через группу счетчиков F. Таким образом, прибор фиксирует остановку мезона в поглотителе.

Для того чтобы отметить распад мезонов, с боков фильтра 3 помещена группа счетчиков Е, регистрирующих электроны или позитроны, появляющиеся при распаде мезонов. Эта группа счетчиков соединена в приборе со всеми остальными группами по схеме запаздывающих совпадений. При этом срабатывание всего прибора происходит только тогда, когда мезон, пройдя через первые два фильтра и застряв в третьем, спустя определенный промежуток времени испускает электрон или позитрон.

Итак, исследователь создал устройство, которое среди частиц различного типа, движущихся с огромными скоростями, отбирало лишь нужные ему μ-мезоны, а среди них - лишь те, которые застряли в фильтре 3. Теперь надлежало измерить, через сколько времени после того как μ-мезон застрял в фильтре и остановился, он распадается и испускает β-частицу.

В первых опытах такого рода при регистрации нужных событий последовательно, шаг за шагом, менялось заранее заданное запаздывание между счетчиками А, В, С, D и счетчиками Е. В последующих опытах Росси и Нерсона вместо этого применялся "электронный секундомер", который позволял измерять интервал времени между остановкой и распадом мюона для каждого отдельного акта распада.

Определенное в результате этих исследований среднее время жизни покоящегося мюона оказалось равным 2,15±0,1 мксек. Легко видеть, что этот результат находится в хорошем согласии с расчетным значением, полученным ранее Росси и Холлом на основе формул теории относительности.

Описанные опыты очень наглядно демонстрируют изменение темпа времени в движущихся телах и необходимость в расширении самого понятия времени в соответствии с теорией относительности.