
5. Распространение звуковых волн
Нас больше всего интересуют те свойства света, которые связаны с его распространением. Чтобы выяснить эти свойства, разберемся в разнице между светом и другими волновыми процессами. Из этих последних нам прежде всего знаком звук. Звук образуется областями сжатия и разрежения, которые распространяются в воздухе со скоростью около 330 м/сек, или около 1200 км/час. Высота того звука, который мы слышим, определяется его длиной волны (и тем самым его частотой). Самые низкие звуки, которые мы слышим, имеют частоту около 20 гц, т. е. их длина волны равна примерно 16 м. (Заметим, что произведение длины волны на частоту равно скорости - в данном случае скорости звука.) Подобным же образом самые высокие доступные нашему слуху звуки имеют частоту около 20 кгц, а значит, длину волны примерно 1 см (для разных людей и для одного и того же человека в разном возрасте эти цифры несколько различаются). Обычно середина диапазона частот нашего голоса приходится на частоту около 1 кгц (длина волны близка к 30 см). Скорость звука нетрудно определить с помощью многих опытов благодаря тому, что она гораздо меньше скорости света. Так, например, глядя на молотобойца, работающего достаточно далеко от нас, мы заметим разрыв между моментами прихода света и прихода звука - ведь свету нужно ничтожное время - микросекунды, чтобы пробежать это расстояние, тогда как звуковая волна должна затратить на это несколько секунд (рис. 6). Поэтому изучить законы распространения звука очень легко.
Рис. 6
Допплеровский сдвиг
Одним из самых интересных и довольно обычных эффектов распространения звука является так называемый допплеровский сдвиг. Если мимо вас по железной дороге на большой скорости мчится гудящий локомотив, то как только он поравняется с вами, звук сирены неожиданно становится более низким. Очевидно, что этот эффект вызван движением локомотива: если бы и источник звука и наблюдатель стояли на одном месте относительно воздуха, то звук, который слышит наблюдатель, имел бы в точности ту же высоту, с которой он был испущен. Причину этого эффекта нетрудно понять, но можно еще упростить задачу, если взять источник звука, движущийся очень быстро, скажем со скоростью, равной половине скорости звука.
Предположим, что скорость звука равна точно 330 м/сек (1200 км/час). Цусть к тому же источник звука движется нам навстречу, а мы, слушая этот звук, остаемся в покое по отношению к воздуху. Рассмотрим источник звука в два момента времени, разделенные интервалом 1 сек. За эту секунду он приблизится к нам на 165 м; звук, испущенный им во второй момент времени, должен пройти на 165 м меньше, чем звук, испущенный в первый момент. Чтобы покрыть эти 165 м, звуку нужно ровно полсекунды. Поэтому второй звуковой сигнал пропутешествует на полсекунды меньше, чем первый, испущенный в первый момент. А поскольку из источника они вышли с интервалом 1 сек, звук, испущенный во второй момент, придет к нам лишь на полсекунды позднее, чем звук, испущенный в первый момент. Значит, вместо того, чтобы воспринимать два звуковых сигнала с разрывом в 1 сек, мы будем воспринимать их как следующие друг за другом с гораздо меньшими интервалами.
В качестве таких сигналов мы можем взять, например, точки высокого давления звуковой волны частотой 1000 гц, которую дает наш источник. Такие вершины (гребни) в этой волне повторяются тысячу раз в секунду, а значит, отстоят друг от друга на миллисекунду. За эту миллисекунду источник пройдет 0,165 м, а звуку, испущенному еще через миллисекунду, потребуется на полмиллисекунды меньше времени, чтобы прийти к нам. Поэтому к нам эти пики давления будут приходить каждые полмиллисекунды, что соответствует частоте 2000 гц. Это значит, что высота звука, воспринятая нами, будет на целую октаву выше высоты звука, испущенного источником. Точно так же нетрудно заметить, что если источник удаляется от нас, то каждому последующему звуковому сигналу придется покрывать все большее расстояние, так что промежутки между приходами последовательных гребней волны будут больше, чем промежутки между моментами излучений этих гребней, и высота звука поэтому понизится. Так объясняется всем известный эффект сирены проносящегося мимо наблюдателя локомотива; этот эффект называют допплеровским сдвигом.
Не так общеизвестно, но важно для нашего дальнейшего изложения, что допплеровский сдвиг частоты неодинаков в случае движения источника относительно воздуха и неподвижного наблюдателя (только что рассмотренный случай) и в случае движения наблюдателя, когда воздух и источник остаются в покое. Допустим, что мы быстро едем на машине навстречу источнику звука со скоростью, равной половине скорости звука. Рассмотрим два звуковых сигнала, испущенных этим источником с промежутком в 1 сек. В какое-то время к нам придет звук, испущенный в первый момент. Посмотрим теперь, что будет через 2/3 сек. Поскольку мы двигались со скоростью, равной половине звуковой (165 м/сек), за это время мы приблизимся к источнику на 110 м. Поэтому звуку, испущенному этим источником, чтобы достичь нас, потребуется на 1/3 сек меньше времени, чем первому звуковому сигналу. Значит, в этот самый момент до нас и дойдет второй сигнал, испущенный через 1 сек после первого, - мы услышим его через 2/3 сек после того, как до нас дошел первый сигнал. Хотя он и вышел на целую секунду позже, уменьшившееся расстояние между нами и источником сократило время его путешествия ровно на 1/3 сек.
Таким образом, двигаясь навстречу источнику Звука, мы будем принимать с промежутками 2/3 сек те сигналы, которые испускались каждую секунду. Мы видим, что теперь частота звука увеличилась на 50%, а не на 100%, как это было в случае движущегося источника, и высота звука возросла не на целую октаву, а лишь на 1/5. Поэтому недостаточно учитывать только скорость движения источника относительно наблюдателя - необходимо знать и скорость источника относительно воздуха, и скорость наблюдателя относительно воздуха. При малых скоростях еще не так важно, кто именно движется, но уж если мы взяли скорость, равную половине звуковой, то это стало весьма существенно.
Звуковая ударная волна
Если описанные выше эффекты были достаточно удивительными при умеренных скоростях, то они становятся совсем необычайными, когда мы превзойдем скорость звука. С появлением сверхзвуковых самолетов это стало совсем обычным делом, и одним из наиболее известных и наиболее прискорбных эффектов сверхзвуковых полетов является ударная волна или, как часто называют это явление, - преодоление звукового барьера. Это явление очень интересно и заслуживает того, чтобы его обсудить.
Рассмотрим сначала (рис. 7) самолет, летящий на постоянной высоте 4 км со скоростью, превышающей скорость звука, например 400 м/сек; напомним, что звук распространяется со скоростью 330 м/сек. Когда самолет находится еще далеко от нас, направленная на нас составляющая его скорости превышает скорость звука. Иными словами, расстояние между нами и самолетом уменьшается быстрее, чем распространяется звуковая волна, так что звук, относящийся к более поздним моментам полета, мы услышим раньше, чем звук, возникший в предыдущие, более ранние моменты. Когда же самолет подойдет к нам ближе, то расстояние от него до нас будет уменьшаться уже далеко не так быстро. В самом деле, это расстояние станет наименьшим, когда самолет очутится точно над нами, а затем оно снова начнет увеличиваться. Поскольку в эти моменты удаление от самолета остается примерно постоянным, так как оно приблизительно равно высоте полета, то расстояние самолета до нас изменяется не так быстро, несмотря на огромную скорость самолета.
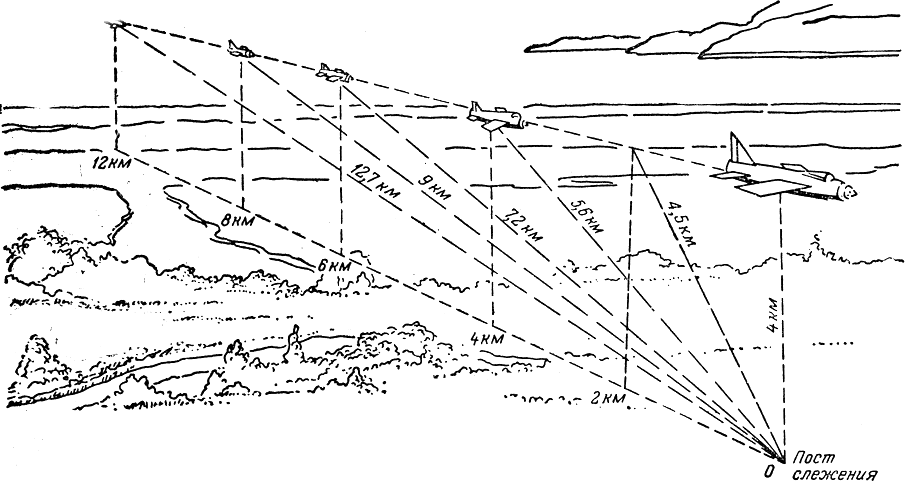
Рис. 7. К обсуждению ударной волны от сверхзвукового самолета
Итак, некоторое время самолет сохраняет примерно одно и то же расстояние от нас. А раз его расстояние до нас уменьшается медленнее, чем распространяется звук, то звук от более поздних моментов полета дойдет до нас позднее, чем от более ранних, как обычно. Значит, дальнюю часть полета самолета мы прослушиваем в обратном порядке, а более близкую (позднюю) часть полета слышим в обычной последовательности. Поэтому сначала мы вообще не слышим этого самолета, а затем до нас одновременно доходит звук сразу со значительной части его пути, потому что там расстояние от самолета до нас уменьшалось точно с такой же скоростью, с которой это расстояние про-ходил звук. Таким образом, гул от самолета за некоторый промежуток времени придет к нам в один и тот же момент. Именно это неожиданное появление звука сразу от целого отрезка пути самолета, ставшее таким оглушительным благодаря сложению всех шумов, и называется ударной волной.
Для большей определенности предположим (см. табл. 1), что, когда наш секундомер показывает 0 сек, самолет находился на таком расстоянии от нас, при котором точка на земной поверхности, находящаяся прямо под самолетом, была удалена от нас ровно на 12 км. Поскольку самолет летел на высоте 4 км, его расстояние от нас было немного больше, а именно 12,7 км; чтобы дойти до нас, звуку требовалось приблизительно 38,5 сек. За следующие 10 сек самолет пролетел около 4 км. Точка, над которой он находился, была от нас уже в 8 км, расстояние между нами и самолетом по прямой составляло около 9 км, и звуку требовалось 27,3 сек, чтобы пройти его. В этом случае звук был испущен на 10 сек позже, чем в предыдущем, так что он пришел к нам через 37,3 сек после 0 секя т. е. за 0,8 сек до того звука, который был испущен десятью секундами раньше. Еще через 5 сек точка, над которой пролетал самолет, была от нас всего в 6 км, расстояние по прямой от самолета до нас равнялось 7,2 км, и звук покрыл его за 21,8 сек, придя к нам еще на полсекунды раньше, чем звук, излученный за 5 сек до этого.
| Момент испускания звука, сек | Координата точки, над которой пролетает самолет, км | Расстояние от самолета до наблюдателя по прямой, км | Время пробега звука, сек | Момент прихода звука к наблюдателю, сек |
|---|---|---|---|---|
| 0 | 12 | 12,7 | 38,5 | 0+38,5 |
| 0+5 | 10 | 10,8 | 32,7 | 0+37,7 |
| 0+10 | 8 | 9,0 | 27,3 | 0+37,3 |
| 0+15 | 6 | 7,2 | 21,8 | 0+36,8 |
| 0+20 | 4 | 5,6 | 17,0 | 0+37,0 |
| 0+25 | 2 | 4,5 | 13,6 | 0+38,6 |
| 0+30 | 0 | 4,0 | 12,1 | 0+42,1 |
Пятью секундами позднее направление на самолет уже составляло с горизонтом 45°, так что самолет пролетал над точкой, лежащей всего в 4 км от нас, а расстояние до него по прямой составляло около 5,6 км, которые звук прошел примерно за 17 сек. Поэтому звук, испущенный тогда самолетом, пришел к нам почти одновременно с тем звуком, который испустил самолет за 5 сек до этого (точнее, он пришел на 0,2 сек позже). Таким образом, до некоторого момента (см. четвертую строку табл. 1) мы вообще не слышали подлетавшего самолета! Еще через 5 сек самолет пролетал над точкой, удаленной от нас на 2 км, по прямой до самолета было 4,5 км, звук прошел их за 13,6 сек и дошел до нас поэтому на 1,6 сек позднее, чем звук, испущенный пятью секундами раньше. Наконец, еще через 5 сек самолет будет прямо над нами, а звук придет с высоты в 4 км через 12,1 сек, т. е. на 3,5 сек позже, чем испущенный за 5 сек до этого. Итак, в течение почти 37 сек с момента начала наблюдения мы ничего не слышали. Потом внезапно, подобно удару, мы услышали звук от целого участка траектории самолета, а затем слышим одновременно два звука: звук, испущенный самолетом после этого момента, и звук, испущенный самолетом раньше, когда он был дальше от нас. Таким образом, гул от самолета, относящийся к моменту начала наблюдения (0 сек) и точке на земле в 12 км от нас, дошел до нас в то же самое время, что и звук, испущенный самолетом, когда он пролетал над точкой, удаленной от нас всего на 2 км.
Часто можно наблюдать еще одно явление. Пусть самолет летел сначала в том же направлении и на той же высоте, что и в предыдущем примере, но скорость его немного меньше скорости звука. Поэтому, хотя он и приближался к нам довольно быстро, звук, соответствующий различным моментам полета, доходил до нас в порядке следования этих моментов друг за другом. Допустим теперь, что самолет стал лететь быстрее, превышая скорость звука, и тогда началась уже рассмотренная нами картина, когда, как мы помним, гул воспринимался в обратном порядке по времени. Между периодом поступления звука в нормальном порядке (дозвуковой полет) и периодом поступления звука в обратном порядке (сверхзвуковой полет) должен быть такой момент, когда мы одновременно услышим звук, пришедший с целого участка пути самолета - новый звуковой удар. Это случится как раз в момент приближения к нам самолета со скоростью звука. Сам он в этот момент будет двигаться немного быстрее звука, так как его путь направлен не точно к нам. Значит, при таком полете будет два звуковых удара, и сначала мы услышим первый из упомянутых здесь. До этого удара мы еще ничего не слышали, а после него мы услышим сразу звук, испущенный в течение трех периодов полета: в дозвуковом полете, пока самолет еще не увеличил свою скорость, поступающий к нам в нормальном порядке; при сверхзвуковом полете на том участке, где самолет был еще далеко от нас, - в обратном порядке по времени; наконец, на последнем участке полета, начиная с того момента, когда самолет был почти прямо над нами, - вновь поступающий в нормальном порядке, но одновременно с двумя предыдущими звуками. Чуть позже мы услышим второй удар, который мы разобрали здесь только что; после него мы будем слышать лишь звук, испущенный этим самолетом, когда он был над нами или уже улетал вдаль.
Разные результаты, получаемые при движении излучателя или приемника звука, следуют из того, что ударные волны могут появиться только при движении излучателя со сверхзвуковой скоростью. Пусть на поверхности земли имеется источник звука и навстречу ему со скоростью, превышающей скорость звука, летит самолет. Его пассажиры не услышат ничего похожего на звуковой удар. Дело в том, что удар случается лишь тогда, когда звук собирается сразу от целого отрезка пути, в один и тот же момент приходя к приемнику. Если бы излучатель покоился относительно воздуха, то, чтобы дать такой эффект, звуковым волнам пришлось бы догонять друг друга, а это никак не может быть, так как скорость звука одна и та же для всех звуковых волн - и никакого удара не произойдет.
Мы хорошо знакомы еще с одним видом волн - с волнами на поверхности воды. Подобно звуковым волнам, они распространяются в среде (воде), но свойства их гораздо сложнее, потому что скорость их зависит от длины волны. Например, волны длиной 450 м (расстояние между соседними гребнями) бегут по океану со скоростью около 100 км/час, тогда как волны, расстояние между соседними гребнями которых составляет всего 30 см, движутся со скоростью только 2,4 км/час. Но несмотря на это различие, на примере таких волн можно проиллюстрировать многие свойства звуковых волн, обсуждавшиеся в этой главе.
|
ПОИСК:
|