10. Кинетическая теория газов

 ●128. Почему не двигалась тележка?

Сосуд, имеющий форму усеченного конуса, установлен на тележке (рис. 69) и заполнен газом. Так как площади АВ и CD различны, то будут различны и силы давления на них газа. Но тогда тележка должна двигаться влево. Однако этого не наблюдается. В чем ошибка рассуждений?

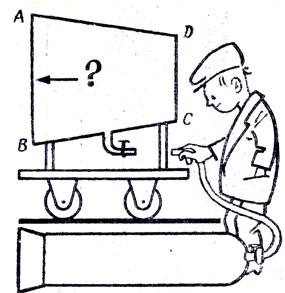
Рис. 69

 ○129. Изотермический процесс.

При изотермическом сжатии идеального газа его температура не изменяется, а следовательно, не изменяется и кинетическая энергия его молекул.

Так как между молекулами идеального газа нет сил притяжения и отталкивания, то при сжатии не изменилась и потенциальная энергия.

Но ведь сжатый газ приобретает способность совершить некоторую работу, т. е. обладает дополнительной энергией. Как разрешить это противоречие?

 ●130. Почему сохраняется температура газа?

По кинетической теории газов температура пропорциональна средней кинетической энергии движения его частиц. Молекулы газа при своем движении сталкиваются друг с другом и со стенками сосуда и в силу иеидеальной упругости теряют при ударе часть своей скорости, так что с течением времени температура газа должна уменьшаться. Сосуд же, содержащий газ, от ударов частиц должен нагреваться. Hto этого на практике не происходит. В чем ошибка рассуждений?

 ●131. Зависит ли конечное состояние газа от порядка выполнения процессов?

Пусть в цилиндре, закрытом поршнем (рис. 70), содержится газ, характеризуемый параметрами: р₀, V₀, t₀^° где t₀^° = 0^°C. Нагреем газ на t^° тогда его объем по закону Гей-Люссака будет равен V₁ = V₀(1γt^°), давление по-прежнему р₀. Создадим дополнительное давление на газ р₁ так, чтобы довести его до прежнего объема V₀. По закону Бойля - Мариотта имеем:

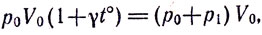
откуда

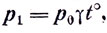
Рис. 70

Охладим теперь газ на t^°, тогда он приобретет прежнюю температуру t^°₀ = 0°C, но объем его станет V₂ = V₀(1-γt°), давление (р₀+p₁). Чтобы довеститаз до прежнего объема, придется снять с поршня некоторое давление р₂. Теперь объем газа V₀, давление (p₀+p₁-р₂), и, следовательно, по закону Бойля - Мариотта

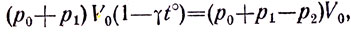
откуда

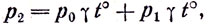
или, принимая в расчет, что 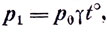получим:

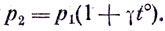
Так как t^°≠0, то р₂≠р₁.

С другой стороны, проследив те изменения, которым мы подвергали газ, убеждаемся, что его конечный объем и температура такие же, как и в начале, поэтому и его давление (p₀+p₁-p₂) должно быть равно прежнему p₀, т. е. должно быть p₀+p₁-p₂ = p₀, откуда p₂ = p₁.

Где в рассуждениях была допущена ошибка?

 ○132. Температура газа.

При резком расширении большинство газов охлаждается (этот эффект используют для сжижения газов). Пусть в сосудах A и В, соединенных краном (рис. 71), содержится идеальный газ (А) и вакуум (В). Открываем кран. Газ врывается в сосуд В и... не охлаждается. Как объяснить этот парадокс?

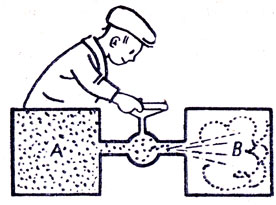
Рис. 71

 ○133. Откуда появилось добавочное давление?

Резервуар А (рис. 72) содержит воздух под давлением больше 1 ат и при температуре окружающей среды. Давление сжатого газа измеряется высотой ртутного столба в манометре. Открыв кран В, выпустили из резервуара столько газа, что ртутный столб в манометре понизился до высоты, соответствующей нормальному давлению. Спустя некоторое время было замечено, что ртуть в манометре снова несколько поднялась. Объясните парадокс.

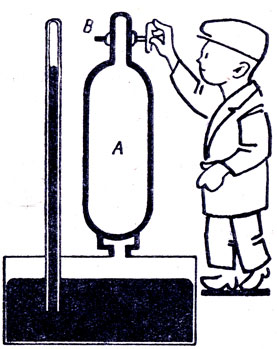
Рис. 72

 ●134. Неравные объемы равны.

Цилиндр А, снабженный поршнем Р (рис. 73), соединяет два неравных по емкости сосуда В и С, содержащие один и тот же газ при температуре 0°С. Пусть начальные объемы газов в сосудах (включая части цилиндра) V_ОB и V_ОС. Нагреем сосуд В на t^° С, а С охладим тоже на t^° С. Тогда поршень Р передвинется на некоторое расстояние по направлению стрелки.

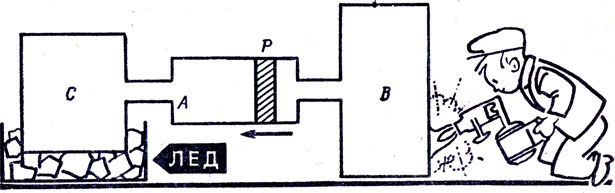
Рис. 73

Рассуждение первое.

Определим увеличение объема газа в сосуде В. Согласно закону Гей-Люссака ΔV₁ΔV_OBγt°. Соответственно уменьшение объема газа во втором сосуде составляет ΔV₂ = - V_OCγt°. Но так как сосуд В, цилиндр А и сосуд С представляют собой единый замкнутый резервуар, то увеличение объема одной его части равно уменьшению объема другой, т. е. ΔV₁ = ΔV₂, или V_OBγt° = V_OCγt°. Следовательно, V_OB = V_OC. Но мы вначале предположили неравенство V_OB ≠ V_OC. Как разрешить противоречие?

Рассуждение второе.

Как бы ни менялись объемы газов в сосудах В и С, общий объем

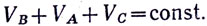
Пусть до изменения температуры суммарный объем был, включая и объем цилиндра, V_OB + V_OC а после нагревания стал V₁ + V₂. Тогда V_0B + V_OC = V₁ + V₂.

Но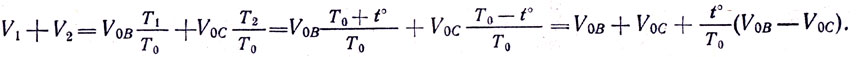

Итак,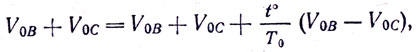

или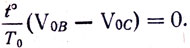

Следовательно, V_OB - V_OC, что также противоречит первоначально сделанному предположению о неравенстве объемов газов в сосудах. В чем ошибки обоих рассуждений?