2. Закон всемирного тяготения

Действуют на все и не знают преград

Одно из самых замечательных свойств сил всемирного тяготения, или, как их часто называют, гравитационных сил, отражено уже в самом названии, данном Ньютоном: всемирные. Эти силы, если так можно выразиться, "самые универсальные" среди всех сил природы. Все, что имеет массу - а масса присуща любой форме, любому виду материи, - должно испытывать гравитационные воздействия. Исключения не составляет даже свет. Если представлять себе наглядно гравитационные силы с помощью ниточек, которые тянутся от одних тел к другим, то бесчисленное множество таких ниточек должно было бы пронизывать пространство в любом месте. При этом нелишне заметить, что порвать такую ниточку, загородиться от гравитационных сил невозможно. Для всемирного тяготения нет преград. Мы можем всегда поставить непреодолимый барьер для электрического поля (таким барьером может служить экран из любого достаточно хорошо проводящего материала); внутрь сверхпроводника, как известно, не проникнет магнитное поле. Но гравитационное взаимодействие свободно передается через любые тела. Экраны из особых веществ, непроницаемых для гравитации (вроде кеворита из романа Г. Уэллса "Первые люди на Луне"), могут существовать только в воображении авторов научно- фантастических книг.

Сравнительно недавно появилось сообщение об измерениях французского астронома Аллена, произведенных во время солнечного затмения. Из анализа этих измерений как будто вытекало, что существует гравитационная тень, что сила притяжения Земли Солнцем уменьшается, когда между ними находится Луна. Что же оказалось в действительности? Просто не было учтено то изменение температуры приборов, которое неизбежно во время затмения. Именно этот, на первый взгляд незначительный эффект и ввел Аллена в заблуждение. Недавно советскому физику В. Брагинскому с рекордной точностью - 10-11 от веса тела - удалось экспериментально доказать отсутствие гравитационной тени.

Велики ли гравитационные силы?

Итак, гравитационные силы вездесущи и всепроникающи. Почему же мы не ощущаем притяжения большинства тел? Почему, например, притяжение Земли чувствуется на каждом шагу, а даже самые высокие горы, эти громады камня, если и притягивают к себе, то разве что только орлов и альпинистов? Если подсчитать, какую долю от притяжения Земли составляет, например, притяжение Эвереста (в самых благоприятных в смысле расположения условиях), то окажется, что лишь тысячные доли процента. Сила же взаимного притяжения двух людей среднего веса при расстоянии между ними в один метр не превышает трех сотых миллиграмма. Так слабы гравитационные силы. Здесь некоторые из читателей, возможно, остановятся в удивлении. Слабы?! Как можно назвать слабым такой "канат", на котором можно подвесить Землю к Солнцу или Луну к Земле, особенно принимая во внимание огромные расстояния между ними? Подобного рода недоумения возникали не раз. Известный популяризатор науки Я. И. Перельман сообщает, например, о появлении в конце XIX века (сравнительно недавно, стало быть) книги Карпентера "Современная наука", автор которой говорил о том, что чрезвычайная слабость гравитационных сил, утверждаемая в физике, вообще подрывает доверие к этой науке. Любопытно отметить, что книга вышла с сочувственным предисловием Л. Н. Толстого.

Гравитационные силы

Тот факт, что гравитационные силы, вообще говоря, гораздо слабее электрических, вызывает своеобразное разделение сфер влияния этих сил. Например, подсчитав, что в атомах гравитационное притяжение электронов к ядру слабее, чем электрическое, в 1 000 000 000 000 000 000 000 000 000 000 000 000 000 раз, легко понять, что процессы внутри атома определяются практически одними лишь электрическими силами (если не касаться пока внутриядерных процессов). Гравитационные силы становятся ощутимыми, а порой и грандиозными, когда на сцену выступают такие огромные массы, как массы космических тел: планет, звезд и т. д.

Так, Земля и Луна притягиваются с силой примерно в 20 000 000 000 000 000 тонн. Даже такие далекие от нас звезды, свет которых годы идет до Земли, шлют нам свой гравитационный привет, выражающийся внушительной цифрой, - это сотни миллионов тонн.

Радиус их действия равен бесконечности

Мы уже фактически молчаливо приняли, что взаимное притяжение двух тел убывает по мере их удаления друг от друга. Это так наглядно и кажется таким очевидным, что редко у кого возникают сомнения на этот счет. Но давайте попробуем мысленно проделать такой опыт: будем измерять силу, с которой Земля притягивает какое-либо тело, например двадцатикилограммовую гирю. Первый опыт пусть соответствует таким условиям, когда гиря помещена на очень большом расстоянии от Земли. В этих условиях сила притяжения (которую, кстати, можно измерять с помощью самых обыкновенных пружинных весов) практически будет равна нулю. По мере приближения гири к Земле появится и будет постепенно возрастать взаимное притяжение, и, наконец, когда гиря окажется на поверхности Земли, стрелка пружинных весов остановится на делении "20 кГ", поскольку то, что мы называем весом, отвлекаясь от вращения Земли, есть не что иное, как сила, с которой Земля притягивает тела, расположенные на ее поверхности. Ну, а если продолжить наш опыт и опустить гирю в глубокую шахту? Легко сообразить, что это уменьшит действующую на гирю силу. Это видно хотя бы из того, что если бы мы, продолжая наш воображаемый опыт, поместили гирю в центр Земли, то притяжение со всех сторон взаимно уравновесилось бы и стрелка пружинных весов стояла бы точно на нуле. Итак, нельзя, оказывается, просто сказать, что гравитационные силы убывают с увеличением расстояния - нужно всегда оговариваться, что сами эти расстояния при такой формулировке принимаются много большими, чем размеры тел. Именно в этом случае справедлив сформулированный Ньютоном закон: силы всемирного тяготения убывают обратно пропорционально квадрату расстояния между притягивающимися телами. Попробуем пояснее представить себе, что это значит. Арифметически это означает, что если, например, расстояние увеличивается в три раза, то сила уменьшается в 3², т. е. в девять раз, ит. д. Однако из этого подсчета еще не ясно, что это - быстрое или не очень быстрое изменение с расстоянием? Означает ли такой закон, что взаимодействие практически ощущается лишь между ближайшими соседями, или же оно заметно и на достаточно больших расстояниях?

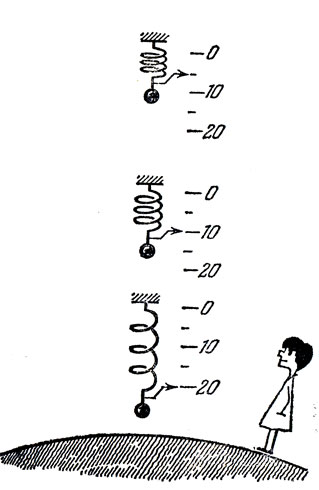
Гиря силы

Ответ на этот вопрос, пожалуй, удобнее всего дать, сравнивая закон убывания с расстоянием гравитационных сил с законом, по которому уменьшается освещенность по мере удаления от источника. Как в одном, так и в другом случае действует, оказывается, один и тот же закон - обратная пропорциональность квадрату расстояния. Но ведь мы видим звезды, находящиеся от нас на таких огромных расстояниях, пройти которые даже световой луч, не имеющий соперников по скорости, может лишь за миллиарды лет! А ведь если до нас доходит свет от этих звезд, значит (закон-то убывания одинаковый) должно, хотя бы и очень слабо, чувствоваться их притяжение. Следовательно, действие сил всемирного тяготения простирается, непрерывно убывая, практически на неограниченные расстояния. Как говорят физики, радиус их действия равен бесконечности. Гравитационные силы - это дальнодействующие силы. Таково "официальное название" этих сил в физике. Далеко не все силы, как мы увидим в дальнейшем, имеют такой характер. Вследствие дальнодействия гравитация связывает все тела Вселенной.

Относительная медленность убывания сил с расстоянием на каждом шагу проявляется в наших земных условиях: ведь все тела не изменяют своего веса, будучи перенесенными с одной высоты на другую (или, если быть более точными, меняют, но крайне незначительно), именно потому, что при относительно малом изменении расстояния - в данном случае до центра Земли - гравитационные силы практически не изменяются.

Кстати, отметим, что именно по этой причине закон изменения гравитационных сил с расстоянием был открыт "на небе". Все необходимые данные черпались здесь из астрономии. Не следует, однако, думать, что уменьшение силы тяжести с высотой нельзя обнаружить в земных условиях. Так, например, маятниковые часы с периодом колебания в одну секунду отстанут в сутки почти на три секунды, если их поднять из подвала на верхний этаж Московского университета (200 метров) - и это только за счет уменьшения силы тяжести.

Высоты, на которых движутся искусственные спутники, уже сравнимы с радиусом Земли, так что для расчета их траектории учет изменения силы земного притяжения с расстоянием совершенно необходим.

Необыкновенное свойство гравитационных сил

В течение многих веков средневековая наука принимала как незыблемую догму утверждение Аристотеля о том, что тело падает тем быстрее, чем больше его вес. Даже повседневный опыт подтверждает это: ведь известно, что пушинка падает медленнее, чем камень. Однако, как впервые сумел показать Галилей, все дело здесь в том, что сопротивление воздуха, вступая в игру, радикально искажает ту картину, которая была бы, если бы на все тела действовало одно только земное притяжение. Существует замечательный по своей наглядности опыт с так называемой трубкой Ньютона, позволяющий прекрасно оценить роль сопротивления воздуха. Вот краткое описание этого опыта. Представьте себе обыкновенную стеклянную (чтобы было видно, что делается внутри) трубку, в которую помещены различные предметы: дробинки, кусочки пробки, перышки или пушинки и т. д. Если перевернуть трубку так, чтобы все это могло падать, то быстрее всего промелькнет дробинка, за ней - кусочки пробки и, наконец, плавно опустится пух. Но попробуем проследить за падением тех же предметов, когда из трубки выкачан воздух. Пушинка, потеряв былую медлительность, несется, не отставая от дробинки и пробки. Значит, ее движение раньше задерживалось сопротивлением воздуха, которое в меньшей степени сказывалось на движении пробки и еще меньше на движении дробинки. Следовательно, если бы не сопротивление воздуха, если бы на тела действовали только силы всемирного тяготения - в частном случае земное притяжение, - то все тела падали бы совершенно одинаково, ускоряясь в одном и том же темпе.

Но "ничто не ново под луной". Две тысячи лет тому назад Лукреций Кар в своей знаменитой поэме "О природе вещей" писал:

 ...все то, что падает в воздухе редком, 
 Падать быстрее должно в соответствии с собственным весом 
 Лишь потому, что воды или воздуха тонкая сущность 
 Не в состояньи вещам одинаковых ставить препятствий, 
 Но уступает скорее имеющим большую тяжесть. 
 Наоборот, никогда никакую нигде не способна 
 Вещь задержать пустота и явиться какой-то опорой, 
 В силу природы своей постоянно всему уступая. 
 Должно поэтому все, проносясь в пустоте без препятствий, 
 Равную скорость иметь, несмотря на различие в весе.

Конечно, эти замечательные слова были только прекрасной догадкой. Чтобы превратить эту догадку в надежно установленный закон, потребовалось множество опытов, начиная с знаменитых экспериментов Галилея, изучавшего падение с известной наклонной Пизанской башни шаров одинаковых размеров, но сделанных из различных материалов (мрамора, дерева, свинца и т. д.), и кончая сложнейшими современными измерениями влияния гравитации на свет. И все это многообразие экспериментальных данных настойчиво укрепляет нас в убеждении, что гравитационные силы сообщают всем телам одинаковое ускорение; в частности, ускорение свободного падения, вызванное земным притяжением, одинаково для всех тел и не зависит ни от состава, ни от строения, ни от массы самих тел.

Этот, повторяем, простой, как будто бы, закон и выражает собой, пожалуй, самую замечательную особенность гравитационных сил. Нет буквально никаких других сил, которые бы одинаково ускоряли все тела независимо от их массы. Вот, например, футболист ударил по мячу. Чем легче мяч, тем большую скорость он получит (при одинаковой силе и длительности удара). Ну, а что бы вы сказали о футболисте, удар которого одинаково ускорял бы как обыкновенный кожаный мяч, так, скажем, и двухпудовую гирю или даже слона? Каждый скажет, что это совершенно невероятно. Но ведь именно так обстоят дела при гравитационных воздействиях, с той только разницей, что, если так можно выразиться, гравитационный "удар" длится непрерывно, никогда не прекращаясь.

Гравитационные силы

О том, какой глубокий физический смысл скрывается за указанной замечательной особенностью гравитационных сил, мы еще будем много говорить при обсуждении вопроса о природе всемирного тяготения, о том, что носит название общей теории относительности. Сейчас нам нужно будет вспомнить, что лежит в основе описания движения в механике. В свое время, говоря об определении силы в механике, мы вынуждены были опереться на ньютоновские законы механики, согласно которым сообщаемое телу ускорение прямо пропорционально действующей на него силе и обратно пропорционально массе тела. Это приводит к простому и замечательному выводу: чтобы ускорение не зависело от массы, необходимо, чтобы сила была пропорциональна массе. Вот, например, два тела: мячик для пинг-понга и такой же по размеру свинцовый шарик. Масса первого примерно в 300 раз меньше массы второго. Значит, чтобы сообщить свинцовому шарику такое же ускорение, как и мячику, на него нужно подействовать в триста раз большей силой. Но под влиянием земного притяжения и мячик и свинцовый шарик падают как раз с одинаковым ускорением. Стало быть, это притяжение отрегулировано в соответствии с массами тел: во. сколько раз масса свинцового шарика больше массы мячика, во столько больше и его притяжение к Земле.

Гравитационные силы

Итак, замечательное свойство сил всемирного тяготения можно спрессовать в одно короткое утверждение: гравитационная сила пропорциональна массе тел. Подчеркнем, что здесь речь идет о той самой массе, которая в законах Ньютона выступает как мера инерции. Ее даже называют инертной массой.

Гравитационные силы

В четырех словах "гравитационная сила пропорциональна массе" заключен удивительно глубокий смысл. Большие и малые тела, горячие и холодные, самого различного химического состава, любого строения - все они испытывают одинаковое гравитационное взаимодействие, если массы их равны.

А может быть, этот закон и действительно прост? Ведь Галилей, например, считал его чуть ли не самоочевидным. Вот его рассуждения. Пусть падают два тела разного веса. По Аристотелю тяжелое тело должно падать быстрее даже в пустоте. Теперь соединим тела. Тогда, с одной стороны, тела должны падать быстрее, так как общий вес увеличился. Но, с другой стороны, добавление к тяжелому телу части, падающей медленнее, должно тормозить это тело. Налицо противоречие, которое можно устранить, только если допустить, что все тела под действием одного только земного притяжения падают с одинаковым ускорением.

Как будто все последовательно! Однако вдумаемся еще раз в приведенное рассуждение. Оно строится на распространенном методе доказательства "от противного": предположив, что более тяжелое тело падает быстрее легкого, мы пришли к противоречию. Заметьте: с самого начала появилось предположение, что ускорение свободного падения определяется весом и только весом. (Строго говоря, не весом, а массой.)

Но ведь это заранее (т. е. до эксперимента) вовсе не очевидно. А что, если бы это ускорение определялось объемом тел? Или температурой? Или, наконец (дадим волю фантазии), цветом или запахом? Короче говоря, представим себе, что существует гравитационный заряд, аналогичный электрическому и, как этот последний, совершенно не связанный непосредственно с массой. Сравнение с электрическим зарядом очень полезно. Вот две пылинки между заряженными пластинами конденсатора. Пусть у этих пылинок равные заряды, а массы относятся как 1 к 2. Тогда ускорения должны отличаться в два раза: силы, определяемые зарядами, равны, а при равных силах тело вдвое большей массы ускоряется вдвое меньше. Если же соединить пылинки, то, очевидно, ускорение будет иметь новое, промежуточное значение. Никакой умозрительный подход без экспериментального исследования электрических сил ничего здесь не может дать. Точно такой же была бы картина, если бы гравитационный заряд не был связан с массой. А ответить на вопрос о том, есть ли такая связь, может лишь опыт. И нам теперь понятно, что именно эксперименты, доказавшие одинаковость обусловленного гравитацией ускорения для всех тел, показали, по существу, что гравитационный заряд (гравитационная или тяжелая масса) равен инертной массе.

Опыт и только опыт может служить как основой для физических законов, так и критерием их точности.

Именно на опыте, на широком испытании природы - от скромных масштабов небольшой лаборатории ученого до грандиозных космических масштабов - основан закон всемирного тяготения, который (если подытожить все сказанное выше) гласит:

Сила взаимного притяжения любых двух тел, размеры которых гораздо меньше расстояния между ними, пропорциональна произведению масс этих тел и обратно Пропорциональна квадрату расстояния между этими телами.

Коэффициент пропорциональности называется гравитационной постоянной. Если измерять длину в сантиметрах, время в секундах, а массу в граммах, гравитационная постоянная будет численно равна 6,68·10^-8, причем ее размерность будет соответственно см³/г·сек².