4. Геометрия и тяготение

Поиски посредника

В одном из своих выступлений великий датский ученый Нильс Бор характеризовал теорию электромагнитных явлений как рациональный выход за рамки классической механики, "пригодный для того, чтобы смягчить контраст между действием на расстоянии и действием при соприкосновении".

Этот контраст еще сильнее в проблеме всемирного тяготения, хотя бы потому, что здесь сами расстояния нередко огромны.

Не каждый, вероятно, сможет разобраться в сложном механизме передачи усилия от руки по цепи к ведру, которое вытаскивают из колодца, но одно ясно для всех: если выпилить из этой цепи хотя бы одно звено, транспортировка силы от руки к ведру прекратится.

А вот гравитационные силы долгое время представлялись именно чем-то вроде удивительной цепи без единого звена. В науке это называется дальнодействием - действием на расстоянии без каких бы то ни было посредников.

Надо прямо сказать, что хотя физики временами "привыкали" к действию на расстоянии и находили его даже удобным, окончательно примириться с тем, что два тела через абсолютно ничем не заполненное пространство (или - это другая крайность - заполненное чем угодно) могут тянуть или толкать друг друга, ученые никогда не могли.

Поиски посредника при гравитационных взаимодействиях начались фактически одновременно с появлением в науке первых догадок об этих силах. Совершенно ясно понимал всю глубину физической проблемы и сам Ньютон.

Казалось бы, можно только удивляться тому, что, сформулировав количественно знаменитый закон о силе всемирного тяготения, Ньютон как будто бы подчеркнуто отвернулся от поисков механизма ее передачи (что дало повод многочисленным комментаторам причислить его к лагерю сторонников дальнодействия). Слово "отвернулся", конечно, неправильно отражает суть дела. А суть эта в следующих двух обстоятельствах.

Прежде всего, Ньютон не мог - просто в силу тогдашнего уровня науки - найти объяснение природы тяготения. Для этого потребовались такие фундаментальные сдвиги в науке, как возникновение понятия поля, о чем подробнее мы расскажем позднее, создание электродинамики и, наконец, теории относительности.

Вторая причина не так очевидна для сегодняшнего исследователя, хотя, вероятно, она сыграла далеко не последнюю роль. Причина эта касается самого понимания естественной науки, ее методов и ее задач.

Многим, вероятно, известна начавшаяся в семнадцатом веке борьба между картезианским и ньютонианским естественнонаучными мировоззрениями. Рене Декарт (Картезий), наряду с Гассенди, Бэконом Веруламским, Гоббсом, Локком и другими выдающимися мыслителями своего времени сумели - и это прежде всего, пожалуй, следует связать с именем Декарта - сделать решительный шаг вперед от господствовавшей в средние века схоластической философии с ее попыткой объяснять природу введением всевозможных "симпатий" и "антипатий", с ее идеей цели в явлениях. Однако, как ни велико было значение новой школы с характерным для нее союзом философии и естествознания, следует признать, что точные науки в современном смысле этого слова возникали нередко в борьбе с этой школой. Теоретические спекуляции Декарта при всем их захватывающем интересе были лишены одного существенного момента - они не только не опирались на опыт, но даже в известной мере противопоставлялись опыту. Именно это явилось поводом к ироническому замечанию Гюйгенса: "Декарт, по-видимому, собирается решать все вопросы физики, не заботясь о том, рассуждает ли он правильно или нет". Характерно в этой связи отношение Декарта к Галилею, которого французский мыслитель упрекал в том, что теперь обозначается словом "эмпиризм". Галилей, по мнению Декарта, не рассматривает первопричины вещей, исследует только основания некоторых отдельных явлений и строит поэтому без фундамента.

"Hipotheses nоn fingo"

Ньютон шел по пути Галилея. Нужно было очистить науку от представлений, не продиктованных самой натурой, прервать бесконечную вереницу гипотез в духе картезианской философии и обратиться к изучению истинных законов природы. Перед вами подлинные слова Ньютона:

"Все, что не вытекает из явлений, является гипотезой. Гипотезам же нет места в экспериментальной физике. В последней выводят некоторые положения из наблюдаемых явлений и обобщают их путем индукции". Именно как отказ от отвлеченных спекуляций картезианской философии следует понимать изречение Ньютона "Hipotheses nоn fingo" - "Гипотез не сочиняю".

Резко отрицательное отношение Ньютона к "сочинительству гипотез" проявилось и в вопросе о природе тяготения. Было бы, однако, глубоко неправильным истолковать это как признание им идеи действия на расстоянии. Впрочем, с полной ясностью об этом высказывается сам Ньютон в письме к Бентли: "Я считаю нелепостью допущение, будто тело, находящееся на некотором расстоянии от другого тела, может действовать на него через пустое пространство без всякого посредства. Поэтому тяжесть должна вызываться каким-то действующим постоянно по определенным законам агентом".

Вопрос о природе этого агента оставался открытым. Не решили его и последовавшие дискуссии, с которыми связаны имена таких выдающихся ученых как Иоганн Бернулли, Гюйгенс, Лейбниц, Даниил Бернулли, Ломоносов, Эйлер.

Одно время имела хождение довольно наивная теория "истечений". Согласно этой теории пространство во всех направлениях пронизывается потоками материи (природа этих потоков не уточнялась). Если представить себе два расположенных неподалеку друг от друга тела, то они как бы загораживают одно другое от этих потоков. Получается так, что с внешней стороны потоки, - а значит, и давление - больше, чем на прилегающих сторонах. Этой-то разницей в давлениях и предлагалось объяснять всемирное тяготение. Вряд ли можно всерьез считать это объяснение удовлетворительным. Оно не только вводит весьма существенные гипотезы, но прямо приводит к выводам, никак не укладывающимся ни в какие экспериментальные рамки. Такое предположение, например, предсказывает несуществующие гравитационные тени или возникновение торможения планет, которого нет в действительности, и т. д.

Хороший вкус человечества

Проблема гравитации вновь - и на этот раз с принципиально новых позиций - была рассмотрена 234 года спустя после окончательного установления Ньютоном закона всемирного тяготения. Для того чтобы сделать здесь новый шаг, оказалось необходимым пересмотреть самые фундаментальные представления - представления о пространстве и времени. В сущности, продвинуться в понимании природы тяготения означало построить новое физическое мировоззрение. И сейчас, задним числом, мы можем поражаться, что такая гигантская работа - а это был, без преувеличений, переворот в физике - могла быть совершена практически одним человеком. Правда, этого человека звали Альберт Эйнштейн. Пожалуй, не будет преувеличением сказать, что ни одна физическая теория никогда не вызывала такого бурного, даже страстного интереса в самых широких кругах как физиков, так и не физиков, как теория относительности Эйнштейна. О ней писали не только в научных журналах и книгах. Не было в двадцатые годы, должно быть, ни одной газеты, ни одного журнала - включая детские журналы и журналы мод, - в котором бы не появилось отзвука этого чисто научного события. Правда, справедливости ради следует отметить, что число писавших о теории относительности всегда значительно превосходило число понимавших эту теорию. Но сам факт огромного интереса массы людей к проблемам гравитации, о которых вчера никто из них не задумывался, несомненно, весьма примечателен. В чем же здесь дело? Ведь созданная Эйнштейном общая теория относительности (о сущности этой теории нам еще предстоит подробно говорить) не имела, да и сейчас не имеет никакого прикладного, практического значения. Она не помогла сконструировать ни одной машины, никого не накормила и не одела, - и тем не менее об Эйнштейне и его теории говорили, спорили и продолжают говорить больше, чем о любом другом ученом, может быть, и очень много сделавшем для удовлетворения практических нужд людей. Дело здесь, конечно, не в "моде" и не в рекламе, и не в том даже, что теория поразила людей своей смелостью и кажущейся парадоксальностью. По-видимому, определяющую роль сыграло здесь то, что теория относительности колоссально раздвинула научные горизонты, затронула фундаментальнейшие философские вопросы естествознания, ставя на повестку дня такие совершенно новые для тогдашней физики проблемы, как, например, проблему связи между пространством, временем и материей. По выражению Инфельда, человечество проявило хороший вкус, должным образом оценив все величие работ Эйнштейна по теории относительности.

Аксиомы Евклида и эксперимент

Однако прежде чем переходить к эйнштейновской трактовке тяготения, нам придется сделать отступление, чтобы познакомиться с некоторыми идеями, которые необходимо будет использовать в дальнейшем.

Нам придется поговорить о геометрии, точнее, о пространстве и времени. Казалось бы, что здесь общего с тяготением? Однако именно исследование физического пространства и времени позволило Эйнштейну по-новому осмыслить гравитацию. Но не будем забегать вперед.

Существует прекрасное изречение, принадлежащее Декарту: "Для того, чтобы познать истину, необходимо один раз в жизни все подвергнуть сомнению, насколько это возможно". Усомниться в том, что кажется само собой разумеющимся, казалось бы, никаких сомнений не допускающим! Суметь прорваться сквозь магический круг так называемых азбучных истин, которые часто только поэтому и кажутся очевидными, что над ними как следует не задумываются.

Много столетий школьники всех стран на уроках геометрии изучали - да и сейчас изучают - стройную систему евклидовых теорем. Все эти теоремы логически вытекают из простейших, таких наглядных, что они кажутся абсолютно достоверными, положений - знаменитых аксиом Евклида.

Школьники на уроках изучают стройную систему евклидовых теорем

Евклидова геометрия вошла в физику целиком без каких бы то ни было оговорок и, фактически, без сомнений в необходимости проверки. Для Галилея и Ньютона пространство - это именно бесстрастный холодный фон. Время течет, как бы подчиняясь ходу каких-то абсолютных мировых часов, отсчитывающих секунды для всей Вселенной, причем на эти часы не может влиять материя и характер ее движения. Этот взгляд на пространство и время казался до начала нашего века незыблемым.

А можно ли проверять самые аксиомы Евклида? Можно ли, например, испытать их справедливость экспериментально? Здесь мыслимы два подхода. Конечно, могут найтись противники такой проверки. Они скажут, что геометрию, как и другие многие разделы математики, следует рассматривать как чисто логическое построение и на этом основании откажутся сравнивать ее положения с опытом. Такая точка зрения вполне правомерна во всех случаях, кроме одного - если вас интересует геометрия "настоящего", реального физического пространства. Но ведь нас-то сейчас интересуют не какие-либо абстрактные "математические" пространства, а именно реальное. А это значит, что последнее слово - и решающее - принадлежит эксперименту. Этим очень многое сказано: эксперимент может и "не захотеть" втискиваться в рамки привычных нам представлений. И тогда уже возникнет необходимость пересмотреть многое из того, что казалось несомненным. Эксперимент, даже если он нацелен на изучение такого "нематериального" объекта, как пространство, в конце концов сводится к наблюдению именно за материей в различных ее формах. И это почти неизбежно (а дальше мы увидим, что слово "почти" излишне) должно привести к установлению связей между поведением материи, с одной стороны, и характером пространства - с другой. Звучит это, разумеется, на первый взгляд довольно фантастично, но если вдуматься, то более привычное нам представление о пространстве (и времени, добавим), как о каком-то бесстрастном, холодном фоне, на котором разыгрываются все события, предстанет перед нами как нечто еще более удивительное и странное.

И, наконец, еще одно. Если уж мы обращаемся к опыту, то нужно ясно отдавать себе ответ в том, что никакой эксперимент не может быть абсолютно точным. Ошибки (или, более деликатно выражаясь, погрешности) опыта, даже самого тонкого, - вещь неизбежная. Они обусловлены несовершенством приборов, случайными влияниями и, порой, самой физической сущностью явления^*. Об этом никогда не забывают в любом физическом исследовании. Будем же и мы постоянно иметь в виду, что какими бы строгими нам ни казались сегодня те или иные теории, в частности "физическая геометрия", о которой мы будем говорить ниже, они имеют приближенный характер, и каждый завтрашний день может внести в них существенные исправления.

^*(Размеры твердых тел, например, никак нельзя определить с ошибкой, меньшей (по порядку величины) межмолекулярных расстояний.)

Геометрия Лобачевского

Мысль о том, что евклидова геометрия не является единственной логически возможной, впервые четко была высказана в прошлом веке. Заслуга создания первой геометрии, отличающейся по своим постулатам от евклидовой, принадлежит великому русскому математику Лобачевскому. (Независимо неевклидова геометрия была разработана венгерским математиком Больяи). Нам сейчас нелегко во всей полноте оценить, какой научной самобытностью и смелостью должен был обладать этот замечательный казанский математик. Факты, однако, достаточно красноречивы. Среди современников оценить (или даже просто понять) идеи Лобачевского смогли, вероятно, три-четыре крупнейших европейских математика, не больше. В России Лобачевский был не понят настолько основательно, что в некрологе, например, много было сказано о его административной деятельности - и ни слова о созданной им новой геометрии. Даже такой передовой человек того времени, как Чернышевский, в письме к сыну выступает против идей Лобачевского, прибегая при этом, увы, к обывательским аргументам вроде того, что Лобачевский недаром, как вся Казань знает, верхом на свинье ездил, так что не приходится сомневаться, что он безумец (мы смягчаем выражения).

Но большие научные идеи не могут заглохнуть, даже если они в момент своего появления казались странными и парадоксальными. Более того, время становится само как бы одним из доказательств их непреложности. К концу девятнадцатого века существовал уже не один, а несколько вариантов неевклидовых геометрий (из них наибольшее значение для физики приобрела впоследствии геометрия Римана). Недоставало, однако, какого-то очень существенного толчка, чтобы эти чисто логические построения "ожили", приобретя трепетность актуальности.

Специальная теория относительности Эйнштейна

Нужен был эксперимент - необычный эксперимент, где объектом исследования была бы геометрия! О таком эксперименте думал Гаусс, келейно (и чуть ли не тайком - ведь из окружающих вряд ли кто-нибудь мог воспринять это иначе как нелепое чудачество) проверявший, равна ли сумма углов треугольника числу п. О нем говорил еще Лобачевский. И эксперимент, нанесший первый удар по привычным представлениям о пространстве и времени, появился. Но он на первый взгляд не имел никакого отношения к геометрии.

Целая серия независимых и разнородных опытов привела к выводу, поразившему физиков своей парадоксальностью: как бы ни двигался наблюдатель, измеряя скорость света, он получал один и тOT же численный результат. Стоите ли вы на месте или пытаетесь догнать световой луч, скорость света оказывается абсолютно одинаковой. От светового луча нельзя убежать, как нельзя убежать от собственной тени. Ту же скорость света покажут ваши приборы, если вы мчитесь навстречу лучу.

Это никак не укладывалось в рамки галилеево- ньютоновых представлений, свидетельствовало об их приближенности и настоятельно диктовало необходимость создания новой теории, которая позволила бы как-то осмыслить этот экспериментальный результат.

Решающий шаг в построении такой новой теории был сделан Эйнштейном.

Теория относительности Эйнштейна

Мы не можем здесь подробно рассказывать об эйнштейновской "специальной теории относительности". Нам нужны будут лишь некоторые ее конкретные результаты. Но прежде всего несколько слов о самой относительности.

Уже Галилей ясно понимал относительность механического движения. Нельзя сказать просто: "тело движется". Нужно указать, по отношению к каким другим телам (физики говорят - по отношению к какой системе отсчета) это движение определяется.

Внешний рисунок движения, конечно, различен в разных системах отсчета. Стенки вагона неподвижны по отношению к системе отсчета сидящих в нем пассажиров. И те же стенки движутся в системе отсчета, связанной с Землей. Траектория вертикально падающего камня выглядит по-разному с точки зрения неподвижного и быстро движущегося наблюдателя. Относительна скорость, относителен путь, пройденный телами, относительна траектория. Но есть и нечто, не зависящее от выбора системы отсчета, - сами законы движения, законы Ньютона. Во всех инерциальных системах эти законы абсолютно одинаковы^*. Это значит, например, что, сидя в закрытой кабине, вы никакими механическими опытами не сможете определить, покоится ли кабина или же равномерно движется. Иначе об этом можно сказать так: все инерциальные системы отсчета равноправны. Нельзя выделить среди них абсолютно неподвижную, как нельзя найти и абсолютно движущуюся.

^*(Инерциальной системой с большой точностью можно считать систему отсчета, центр которой связан с Солнцем, а оси направлены на неподвижные звезды, или любую другую систему, которая движется с постоянной скоростью относительно этой системы.)

Эйнштейн обобщил этот принцип, распространив его не только на механику, но и на любые другие процессы. Экспериментальный факт постоянства скорости света был принят им как второе исходное требование, которому должна удовлетворять новая теория.

Для дальнейшего нам понадобится лишь одно из важных следствий теории относительности Эйнштейна, а именно, так называемое лоренцово сокращение длин. Если измерить длину какого-то стержня в системе отсчета, где он покоится, а затем в другой системе, по отношению к которой этот стержень движется (в продольном направлении), то вторая длина окажется меньше, чем первая. И дело здесь не в том, что нечто меняется внутри самого стержня. С таким же успехом можно рассмотреть не стержень, а просто две независимые частицы, расположенные достаточно далеко друг от друга. Меняется сама геометрия, происходит изменение самого масштаба длин в направлении движения.

Заметим, кстати, что ход часов также существенно различен в различных инерциальных системах отсчета. Быстрее всего часы идут в той системе, относительно которой они покоятся. В любой другой системе время течет медленнее, и это (равно как и сокращение длин) тем ощутимее, чем больше приближается скорость системы к скорости света. Кстати, именно потому, что механика Галилея - Ньютона родилась из наблюдений за движением сравнительно медленно перемещающихся тел (со скоростями много меньшими, чем скорость света, равная почти тремстам тысячам километров в секунду), оказалось возможным говорить о едином - абсолютном - времени и игнорировать сокращение длин.

Принцип эквивалентности

Однако какая связь может быть между относительностью длин и проблемой тяготения? Вот к этому вопросу мы сейчас и перейдем. Помнит ли читатель то, что в начале этой главы было названо "удивительным свойством гравитационных сил"?

Тяжелая и инертная массы равны!

Все тела, независимо от их природы и массы, приобретают под действием гравитационных сил совершенно одинаковые ускорения. Чем же это объясняется? Ведь нельзя же, в самом деле, ссылаться на случайные совпадения - уж слишком знаменателен сам факт.

Размышляя над этой проблемой, Эйнштейн обратил внимание на обстоятельство, которое, конечно, уже давно было прекрасно известно всем физикам, но которое никому не приходило в голову связать с гравитацией. Чтобы понять, в чем здесь дело, представьте себе, что вы находитесь в кабине свободно летящего (с выключенными двигателями) космического корабля. Наступило состояние невесомости. Все обстоит так, как если бы никакого тяготения вообще не было. Маятник замрет в отклоненном положении, выплеснутая из стакана вода большой сферической каплей повиснет в воздухе и рядом с ней застынут, будто подвешенные на невидимых нитях, все остальные предметы, независимо от их массы и формы. Вы подтолкнули тяжелую гирю и она плавно поплыла, пересекая кабину. Если бы не сопротивление воздуха, ее движение было бы абсолютно равномерным.

И все это, заметьте, вовсе не требует того, чтобы сам космический корабль находился вдали от звезд и планет, чтобы до него не дотягивалось их гравитационное воздействие. Невесомость возникает, например, на всех космических кораблях, совершающих полет вокруг земного шара. Ведь эти корабли, совершенно очевидно, находятся в сфере действия почти таких же гравитационных сил, что и на поверхности Земли. И космонавт не ощущает этих сил по следующей сравнительно простой причине. Движение космического корабля складывается из равномерного движения по горизонтали и ускоренного падения по вертикали, к центру Земли. О том, что заметить равномерное движение по поведению вещей внутри кабины невозможно, уже говорилось. Что же касается падения, то все предметы в кабине действительно падают под действием притяжения Земли. Но падают - напомним - с совершенно одинаковым ускорением. И точно с таким же ускорением, падают пол, стенки и потолок кабины. Космонавт упал на один метр, - но ровно на метр ушло из-под него кресло. В результате он может свободно висеть над сиденьем.

Иначе говоря, гравитационные силы, явственно проявляющиеся в связанной с Землей системе отсчета, исчезают, если перейти в свободно падающую систему (только, разумеется, они исчезают не одновременно во всем пространстве вокруг Земли, а лишь в ограниченном пространстве кабины^*).

^*(Было бы неправильно думать, что здесь стенки кабины играют какую-то роль гравитационных границ. Размеры области, в которой перестает ощущаться гравитация, определяются не размерами кабины, а расстояниями, на которые можно переместить любое тело, не заметив изменения гравитационных сил по величине и направлению.)

Слово "исчезают" мы употребили здесь не случайно. Действительно, никаким опытом, какие бы приборы мы ни применяли, какое бы явление ни рассматривали, невозможно обнаружить даже признаков тяготения, находясь в закрытой падающей кабине (физики часто говорят, следуя Эйнштейну, о "падающем лифте").

Притяжение Земли

Заметим попутно, что с этим явлением мы непрерывно сталкиваемся, даже и не садясь в кабину звездолета. Ведь наша Земля - это тоже огромный космический путешественник, она вместе со всеми ее обитателями движется, направляемая притяжением Солнца. А мы этого притяжения не чувствуем. Причиной является не малость эффекта, а опять-таки тот факт, что движение Земли по ее орбите представляет собой, в сущности, непрерывное падение^*.

^*(Движение кораблей-спутников вокруг Земли и Земли вокруг Солнца в несущественных деталях не похоже на простое падение. Во втором случае движение прямолинейно. Это различие можно обнаружить на опыте, поставленном внутри кабины.)

Только приливы, о которых мы уже рассказывали раньше, служат непрерывным зримым напоминанием о притяжении со стороны Солнца и Луны.

После всего сказанного встает вопрос: если за счет перехода в ускоренную систему отсчета можно убрать гравитационные силы, то нельзя ли таким же способом и создавать их? С одной стороны, как будто можно. Например, если механик будущего межзвездного корабля отрегулирует двигатель таким образом, чтобы за каждую секунду скорость возрастала примерно на десять метров в секунду, то команда окажется точно в таких же гравитационных условиях, как и все люди на Земле. С другой стороны, однако, невольно возникают сомнения. Так и кажется, что здесь какой-то суррогат тяготения. Но любая подделка, как бы она ни была совершенна, чем-нибудь отличается от настоящего, а у нас ни в чем, буквально ни в чем нет никаких отличий. Ведь основное свойство сил тяготения - то, что они совершенно одинаково ускоряют любые тела. Это свойство в ускоренно движущейся системе обеспечивается, если так можно выразиться, автоматически. У всех тел с точки зрения такой системы появляются добавочные одинаковые ускорения, равные по величине и противоположные по направлению тому ускорению, которое сама эта система имеет с точки зрения инерциальных систем.

Итак, взвесив все обстоятельства, мы убеждаемся, что можно отважиться на следующее исключительно важное утверждение: в каждой достаточно малой^* области пространства никакими физическими экспериментами невозможно отличить движение тел под действием гравитационных сил от их движения в соответствующим образом подобранной ускоренной системе. Или, более коротко: тяготение в каждой точке пространства эквивалентно соответствующим образом подобранному ускорению системы отсчета. Эквивалентность, по Эйнштейну, касается не только механических движений, но вообще любых процессов.

^*(Область пространства считается здесь малой, если гравитационное воздействие не изменяется при перемещении тела внутри этой области. Ясно, например, что огромный зал Дворца спорта в Лужниках с этой точки зрения с большим запасом точности - достаточно малая область. В то же время вся Земля уже не может составить такую область - здесь нельзя игнорировать изменения гравитационных сил по величине и по направлению.)

Мы пришли, таким образом, к знаменитому принципу эквивалентности Эйнштейна, являющемуся одной из самых глубоких гипотез в современной теории принципу, который, как мы сейчас убедимся, с неизбежностью приводит к установлению теснейшей связи между гравитацией и геометрией.

В поле тяготения геометрия не может быть евклидовой

Необходимость такой связи очевидна хотя бы из такого простого рассуждения: в привычной нам геометрии Евклида (по причинам, которые нам станут понятными позднее, ее называют "плоской" геометрией) отношение длины окружности к диаметру равняется числу "пи" (π = 3,14...). Его можно получить, разделив число очень маленьких стержней, уложенных вдоль окружности, на число стержней, уложенных вдоль диаметра. А теперь посмотрим, чему равно это отношение с точки зрения системы отсчета, вращающейся вместе с окружностью. Пусть экспериментатор в этой системе отсчета начнет укладывать те же самые стержни вдоль окружности и диаметра. Результат, к которому он придет, можно установить, рассматривая этот измерительный процесс с точки зрения инерциальной системы. Каждый стержень на окружности согласно теории относительности сокращается, в то время как стержни вдоль диаметра не должны испытывать сокращения. Ведь их направления перпендикулярны скорости движения. Значит, движущийся экспериментатор уложит по окружности большее число стержней, чем неподвижный, а вдоль диаметра - то же самое число. Поэтому отношение длины окружности к диаметру во вращающейся системе отсчета больше π. Но ведь это возможно лишь в том случае, когда изменилась сама геометрия, если она перестала быть евклидовой! И, что очень интересно, характер новой геометрии однозначно определяется тем ускорением, с каким движутся отдельные точки системы отсчета.

Сделаем теперь еще один шаг - и мы у цели. Приняв принцип эквивалентности, мы тем самым согласились считать, что все результаты, которые получаются в ускоренно движущихся системах, будут иметь место в инерциальных системах при наличии тяготения. Но если так, то само тяготение можно рассматривать как отступление от евклидовой геометрии, "искривление пространства", как мы будем для краткости говорить в дальнейшем.

Вывод, самый, пожалуй, удивительный из всех, которые знала физика за все время своего существования, сделан: тяготение связано с искривлением пространства! Роль того агента, о котором говорил в свое время еще Ньютон, который картезианцами связывался с таинственными вихрями, существующими между телами, принадлежит, оказывается, свойствам самого пространства, его геометрии.

Попытаемся на простейшей модели внести в этот абстрактный и чрезвычайно сложный вывод хотя бы некоторый элемент наглядности.

Геометрия двумерных существ

Представьте себе растянутую резиновую пленку с нанесенной на ней сеткой. Она будет играть роль координатной сетки. Это - модель пространства (но только не трех, а двух измерений), обладающего евклидовыми свойствами. Если представить себе, что на этой пленке обитают какие-то фантастические двумерные существа, обладающие к тому же интеллектом, то среди них рано или поздно должен появиться свой Евклид, который сформулирует основы геометрии, которые будут точно такими же, как обычная геометрия Евклида на плоскости.

Но вот мы надавили пальцем на какой-то участок пленки. Этот участок растянулся, изменились углы между линиями, отношение длины окружности к диаметру перестало быть равным я, сумма углов треугольника сделалась отличной от я, - одним словом, произошло то, что двумерные геометры с неизбежностью должны истолковать как нарушение евклидовой геометрии, как искривление пространства. Заметьте, все эти явления сказываются тем сильнее, чем ближе участок пленки к возмущающему телу - в нашем примере к оказывающему давление пальцу.

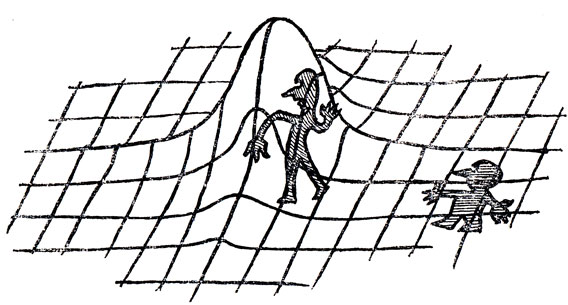
Геометрия двумерных существ

Может появиться соблазн продолжить аналогию с пленкой еще дальше. В самом деле, почему бы не сравнить действие пальца, надавливающего на пленку, с действием масс, вызывающих тяготение. Тем более, что от давления пальца в одном месте пленки во всех других местах появляются соответствующие упругие натяжения, которые так и хочется сравнить с гравитационными силами (они, кстати, даже убывают с расстоянием почти так же, как тяготение). Однако эту аналогию нельзя считать очень глубокой. Ни с какой упругостью гравитация, конечно, не связана. Сходство начинается и кончается чисто геометрической стороной дела.

Что такое прямая линия?

Можно подойти к необходимости связать геометрию с тяготением и с другого конца. Среди аксиом Евклида есть одна, которая гласит: через две точки можно провести только одну прямую линию. Это, так сказать, одна из тех азбучных истин, которые, следуя Декарту, мы тоже попытаемся подвергнуть сомнению. Прямая линия... Вдумайтесь: а что это, собственно, такое - прямая линия?

Конечно, было бы наивно ответить, что прямая линия - это линия, проведенная по линейке. Нужно еще как-то предварительно проверить, не искривлена ли сама линейка.

Может быть, некоторые из читателей вспомнят, что прямая - кратчайшее расстояние между двумя точками. Но им сразу же придется подумать над тем, как, собственно, измерять расстояния. Для этого опять потребуется линейка, причем прямая линейка. Получается порочный круг.

Можно было бы, конечно, попытаться говорить о натянутых нитях. Не даром же говорят: "...прямой как струна". Но это завело бы нас в такие дебри проблем теории упругости, которые лучше обойти стороной.

Есть и еще один - простейший - способ определения прямых. Человек уже давным-давно пользуется световыми лучами как идеально прямыми линиями. Что вы делаете, чтобы проверить, не искривилась ли линейка? Подносите ее к глазам и смотрите вдоль ребра, т. е. сравниваете ребро линейки со световым лучом. По существу, где бы ни применялась геометрия в практике людей, а это делается буквально на каждом шагу, используется этот же принцип. Он так прост, что над ним не задумываются.

Прост ли? Как практический способ - конечно. Но за этой простотой скрывается очень глубокий физический смысл.

Чтобы применять какой-либо эталон, нужно быть уверенным, что на него не оказывает действия окружающая среда, что он стабилен. Как показывает глубокий теоретический анализ, световой луч в высочайшей степени обладает такой стабильностью: он не испытывает никаких воздействий^*. Впрочем, это не совсем точно. Есть одна сила, которая влияет и на свет. Замечательно, что это - гравитация. Да, именно сила всемирного тяготения еще раз оправдывает свое название: влияние гравитации на свет теперь доказано прямыми опытами.

^*(Сказанное не противоречит явлению отражения и преломления волн: эти процессы сводятся к многократным поглощениям и испусканиям волн. Между испусканием же и поглощением световая волна действительно не испытывает воздействий.)

Искривление световых лучей

Астрономы, наблюдая звезды, точно определяют их положение на небосводе и наносят на звездную карту. И недаром звезды называются неподвижными. Звездная карта, составленная сотню лет назад, с высокой степенью точности совпадает с сегодняшней. К этому все, казалось, привыкли. Но вот Эйнштейн выступил с удивительным предсказанием: во время солнечного затменения все звезды, расположенные вблизи затененного Луной солнечного диска, должны смещаться, как бы отодвигаться от Солнца. Такое смещение действительно было обнаружено. Простое и наглядное объяснение этого явления появится сразу, если принять, что световые лучи отклоняются под влиянием гравитации в сторону Солнца. Действительно, пусть луч от звезды, идущий к Земле, проходит вблизи Солнца (ясно, что притяжение Солнца скажется заметно лишь на малых расстояниях) и испытывает отклонение. Земной наблюдатель, который увидел бы звезду в центре окуляра, если бы луч света не проходил возле Солнца, теперь увидит ее в центре поля зрения окуляра, только немного отклонив телескоп от Солнца. Эйнштейновская теория хорошо количественно и, хочется сказать, естественно описывает отклонение световых лучей под влиянием гравитации, предсказывая углы отклонения, очень близкие к тем, которые измеряют астрономы.

Искривление световых лучей

Мы не можем входить здесь в детали подтверждающих это количественных расчетов. Попытаемся, однако, показать, что если верен эйнштейновский принцип эквивалентности, то световой луч с неизбежностью должен отклоняться. Начнем со сравнения. Представьте себе, что вы едете в поезде. Идет дождь, и капли прочерчивают полоски на стеклах. Если поезд движется равномерно, то полоски будут прямыми. При ускоренном же движении они изогнутся (искривление!). Любые другие струйки будут также искривляться с точки зрения пассажиров набирающего скорость поезда. Не составляют исключения и световые струи.

А теперь вспомним, что в согласии с принципом Эйнштейна ускорение эквивалентно наличию тяготения. Следовательно, искривление световых лучей (и, добавим, лучей, образованных потоками любых частиц) под влиянием тяготения неизбежно.

Как была "взвешена" электромагнитная волна

Второй опыт, доказывающий влияние гравитации на свет, имеет вполне земной характер и масштабы. Читатель знает, что для того, чтобы услышать передачу радиостанции, нужно настроить приемник на ее волну. А вот такая мысль, вероятно, возникала не у всех: не нарушится ли настройка, если взобраться с приемником на высокую гору или опуститься в низину? "Конечно, не нарушится", - скажете вы. Какую же роль может играть такой подъем или спуск? Вот какую: сначала настройка велась на одном уровне, а потом, когда приемник был поднят, электромагнитные волны от передатчика к приемнику пойдут вверх, преодолевая силы земного тяготения. Опыт показывает, что действительно они при этом будут терять энергию и одновременно будет уменьшаться их частота. Конечно, у обычных приемников и передатчиков настройка настолько груба, что заметить такое явление невозможно. Однако недавно физикам удалось отыскать сверхточно настроенные приемники и передатчики. Не думайте, что речь идет об устройствах обычного радиотехнического типа; в данном случае и приемник, и передатчик представляли собой особые кристаллы, в состав которых входили атомы с ядрами, способными испускать и поглощать электромагнитные волны очень большой энергии - так называемые γ-кванты с очень точно фиксированной частотой. В опытах Мёссбауэра, поставленных по этой схеме, оказывалась достаточной разность уровней в десяток метров, чтобы заметить "ускорение"^* падающего вниз луча. Эти, отметим кстати, рекордные по точности опыты являются прямым доказательством того, что свет "весит", что на электромагнитные волны, как и на все другие виды материи, оказывает влияние гравитация.

^*(Конечно, это "ускорение" не надо понимать з обычном механическом смысле слова. Имеется в виду не увеличение скорости света - она в пустоте (в воздухе практически то же самое) строго постоянна, - а рост энергии.)

Спектральные линии света, идущего от звезд, немного сдвинуты в сторону красного конца спектра, причем этот сдвиг тем заметнее, чем больше масса звезды. Это, в сущности, тот же опыт Мёссбауэра, только в космическом масштабе. Он иногда применяется для измерения массы звезд. Этот эффект, как и искривление лучей, проходящих вблизи массивных тел, был предсказан Эйнштейном.

Урок геометрии на фантастической планете

А теперь сопоставим все сказанное выше. Мы установили, что лучшим из эталонов прямой является световой луч в пустоте. В то же время этот луч под влиянием гравитации - только гравитации - отклоняется или, если хотите, искривляется. Вот мы опять, но уже с новых позиций, пришли к тому же результату, что и раньше. Только тогда мы говорили об искривленном пространстве, а теперь употребляем выражение: искривленные прямые.

Вывод о неразрывной связи между тяготением и искривлением пространства, сделанный Эйнштейном, явился в свое время буквально ошеломляющим. Слишком уж неожиданным и значительным он казался всем, кто задумывался над проблемой тяготения. Но, пожалуй, прежде всего неожиданным и необычным.

Вспомним опять школьные уроки геометрии. Ведь учитель не упоминал там ни о каком тяготении. Он не говорил, например, что через две точки при определенной величине гравитационных сил можно провести только одну прямую! Да, не говорил, но это лишь потому, что геометрия Евклида выросла из практики людей, живущих на Земле, где влияние тяготения на геометрию настолько мало, что даже сейчас, используя современное оборудование, очень трудно - почти невозможно - заметить неточность этой геометрии.

А теперь мысленно перенесемся на такую планету (допустим, что она существует), где сила тяготения в десятки миллионов раз больше, чем у нас. Можно придумать такие условия, что направленный горизонтально луч света не сможет преодолеть притяжения и будет огибать планету параллельно ее поверхности как спутник. И если далее, дав волю фантазии, представить себе, что на этой планете есть школы, то на уроках геометрии учитель должен бы, вероятно, говорить примерно следующее: "Свет в пустоте движется по прямой. Представим себе сильнейший прожектор, подвешенный над одним из полюсов и посылающий пучок лучей по горизонтали. Допустим, что нет ни рассеяния, ни преломления, ни поглощения света. Тогда лучи, пройдя над поверхностью планеты, дойдут до второго полюса и, миновав его, вернутся - только с другой стороны - к прожектору. Немного повернув прожектор, вы получите другой луч - другую прямую, также проходящую через оба полюса. И таких прямых можно получить сколько угодно. Они очень похожи на меридианы, соединяющие полюса. Итак, дети, вы видите, что через две точки - в данном случае через два полюса - можно провести бесчисленное множество прямых линий. Запомните эту аксиому - она является одной из основ геометрии. Сообщу вам, дети, не вдаваясь в подробности, что математики додумались до такой геометрии, где через две точки проходит только одна прямая, - но вряд ли это может найти какое-либо практическое применение".

Ученики выучат это положение, будут, отвечая урок, говорить, что параллельные линии пересекаются, что сумма углов треугольника не равна числу ли после окончания школы в своей практической деятельности никогда не столкнутся ни с какими геометрическими парадоксами.

Можно было бы еще много рассказывать об этой удивительной планете, где, например, каждый, в принципе, может безо всяких зеркал увидеть собственный затылок, но, пожалуй, пора вернуться на Землю. Наше воображаемое путешествие было поучительным: мы убедились еще раз, что привычное не обязательно должно быть всеобщим и единственно возможным. Оказывается, даже геометрия не составляет исключения.

Еще одна порция сомнений

Нам остается добавить еще лишь одно. Вдумчивый читатель мог бы заметить, что во всех наших рассуждениях о световых лучах есть некий элемент наивного практицизма. На практике, - говорим мы, - световой луч является эталоном прямой линии, а поскольку он искривляется гравитацией, то, значит, сама гравитация связана с искривлением геометрии. Не слишком ли сильное ударение мы делали на словах "на практике"?

Ведь таким способом, ссылаясь на "практику", можно оказаться в сетях самых примитивных противоречий. "На практике" тот кусок Земли, который охватывает наш взгляд, является примерно плоским. Но ведь мы же не можем из этого сделать вывод, что вся Земля - плоская. "На практике" ложечка в стакане с чаем кажется изломанной, но ведь мы умеем, учитывая преломление света на границе между водой и воздухом, восстановить истинную картину. Нельзя ли аналогичным образом учесть и то "преломление" световых лучей, которое вызывается тяготением, и ввести соответствующую поправку?

Но что значит - ввести поправку? У нас есть способы убедиться, что Земля шарообразна, а ложечка в стакане не переломлена. Способы экспериментальные. Например, если подняться, как это было сделано космонавтами, на достаточно большую высоту, то с этой новой точки зрения шарообразность Земли становится заметной на глаз. А где же найти ту "точку зрения", которая позволила бы отсепарировать геометрию от тяготения? Какой опыт мог бы доказать, например, что "на самом деле" прямые остаются прямыми, пространство - "плоским", а искривляются лишь световые лучи? Ведь для такого опыта потребовался бы какой-то абсолютный эталон прямизны. Но его-то как раз и нет!

Но суть даже не в этом. Внимательный читатель мог бы задать еще и такой вопрос. Представим себе на минуту, что вообще никакого эталона прямых линий не существует, что, например, на Земле все линейки - кривые и мы не умеем их спрямить. Что же - разве от этого наша земная геометрия станет менее похожа на евклидову? Разве от того, что мы пользуемся не привычной прямоугольной декартовой координатной сеткой, а криволинейной географической сеткой параллелей и меридианов, сумма углов треугольника как-то меняется? Да конечно же нет! Так в чем же дело?

Дело, разумеется, опять в принципе эквивалентности. Вспомните рассуждения о вращающемся диске, с которого мы начинали наш рассказ^*. Ведь здесь существенно не то, что какие-то прямые линии стали кривыми, а то, что нарушены сами геометрические соотношения: отношение длины окружности к ее радиусу стало иным, чем то диктуется геометрией Евклида. И в силу принципа эквивалентности тот же эффект должен производиться силами всемирного тяготения (конечно, соответственно подобранными).

^*(Упомянем, что пример с диском позволяет также показать влияние тяготения на ход часов. Действительно, чем дальше расположены часы от центра вращающейся системы, тем больше их скорость, а значит, тем медленнее они идут. Но, с другой стороны, ускорение также увеличивается с ростом расстояния от центра. На основе принципа эквивалентности мы, стало быть, сразу сможем сделать вывод: чем сильнее тяготение в том месте, где находятся часы, тем медленнее они идут. Соответственно можно говорить об искривлении времени в том же смысле, что и об искривлении пространства.)

А искривление светового луча, которое мы использовали для наглядной иллюстрации того, что собой представляет физическая геометрия, - это не причина, а следствие искривления геометрии.

"Притча Эддингтона"

Вернемся теперь еще раз к закону всемирного тяготения. Мы так долго искривляли пространство, что может показаться, будто забыто, ради чего, собственно, и пошел весь разговор. Нет, конечно, не забыто. Более того, все предыдущее, по существу, и является новым толкованием тяготения.

Хорошо это иллюстрирует притча английского физика Эддингтона из книги "Пространство, время и тяготение", которую мы позволим себе пересказать (с небольшими комментариями в скобках).

"В океане, имеющем только два измерения, жила однажды порода плоских рыб. Было замечено, что рыбы вообще плавали по прямым линиям, пока они не встречали на своем пути явных препятствий. Это поведение казалось вполне естественным. Но в океане была таинственная область; когда рыбы в нее попадали, они казались заколдованными; некоторые проплывали через эту область, но изменяли направление своего движения, другие без конца кружились по этой области. Одна рыба (почти Декарт) предложила теорию вихрей; она говорила, что в этой области находятся водовороты, которые заставляют кружиться все, что в них попадает. С течением времени была предложена гораздо более совершенная теория (теория Ньютона); говорили, что все рыбы притягиваются к очень большой рыбе - рыбе-солнцу, дремлющей в середине области, - и этим объясняли отклонение их путей. Вначале эта теория казалась, быть может, немного странной; но она с удивительной точностью подтвердилась на самых разнообразных наблюдениях. Было найдено, что все рыбы обладают этим притягивающим свойством, пропорциональным их величине; закон притяжения (аналог закона всемирного тяготения) был чрезвычайно прост, но, несмотря на это, он объяснял все движения с такой точностью, до которой никогда раньше не доходила точность научных исследований. Правда, некоторые рыбы, ворча, заявляли, что они не понимают, как возможно такое действие на расстоянии; но все были согласны, что это действие распространяется при помощи океана и что его легче будет понять, когда лучше будет изучена природа воды. Поэтому почти каждая рыба, которая хотела объяснить притяжение, начинала с того, что предполагала какой-нибудь механизм, при помощи которого оно распространяется через воду.

Но была рыба, которая посмотрела на дело иначе. Она обратила внимание на тот факт, что большие рыбы и малые двигались всегда по одним и тем же путям, хотя могло казаться, что для отклонения большой рыбы с ее пути потребуется большая сила. (Рыба-солнце сообщала всем телам одинаковые ускорения.) Поэтому она вместо сил стала подробно изучать пути движения рыб и таким образом пришла к поразительному решению вопроса. В мире было возвышенное место, где лежала рыба-солнце. Рыбы не могли непосредственно заметить этого потому, что они были двумерны; но когда рыба в своем движении попадала на склон этого возвышения, то хотя она старалась плыть по прямой линии, она невольно немного сворачивала в сторону. (Когда путешественник передвигается по левому склону горы, он должен сознательно уклоняться влево, если он хочет сохранять свое первоначальное направление по компасу.) В этом состоял секрет таинственного притяжения или искривления путей, которое происходило в таинственной области.

Между тем, о чем рассказывается в этой притче, и тем, что нас интересует, нет, конечно, полной аналогии, потому что то возвышение, о котором в ней говорится, относится только к пространству, в то время как нам приходится иметь дело с "возвышением" в пространстве - времени. (В нашей книге мы не можем останавливаться на этом подробнее.) Но эта притча показывает, как кривизна мира, в котором мы живем, может дать иллюзию силы притяжения, и мы видим, что эффект, подобный притяжению, есть единственное, в чем такая кривизна может проявиться".

Коротко это можно формулировать следующим образом. Так как гравитация одинаковым образом искривляет пути всех тел, мы можем считать тяготение искривлением пространства - времени. Тяготение - "alter ego"^* искривления геометрии.

^*(Другой я.)

С кривизной пространства - времени можно не связывать ничего, кроме искривления пространственно-временных путей (так называемых мировых линий^* всех без исключения тел.

^*(Под мировой линией понимается кривая, изображающая зависимость координат движущейся точки от времени. Для простейшего одномерного движения - движения вдоль пространственной прямой - мировая линия изображает зависимость единственной координаты от времени. При равномерном движении мировая линия будет прямой; при ускоренном движении она искривляется.)

Движение перигелия Меркурия

Мы провели длинные рассуждения и пришли к существенно новому пониманию тяготения. Разумеется, это само по себе важно и интересно. Но, может быть, ничего существенного нам это не дает и на "выходе" остается все тот же старый добрый ньютоновский закон?

Конечно, это не так. Речь идет не только о новом осмысливании старых истин, но и о принципиальных обобщениях, о новых эффектах.

О том, что теория Эйнштейна количественно верно описывает отклонение световых лучей под влиянием тяготения, и об эффекте Мёссбауэра мы уже говорили. Можно упомянуть и об успешном объяснении движения перигелия планет, особенно Меркурия. Имеется в виду следующее. Подсчет по законам ньютоновской механики приводит к выводу, что орбиты всех планет должны быть эллипсами, положение которых в пространстве неизменно. Наблюдения же показывают, что эти орбиты медленно поворачиваются. Наиболее заметно это у Меркурия, ближайшей к Солнцу планете, испытывающей, следовательно, наибольшее гравитационное влияние. Расчет, основанный на эйнштейновской теории тяготения, дает хорошее количественное описание этого явления.

Гравитационные волны

Все, о чем мы говорили выше, имеет, если угодно, характер малых поправок. Существует, однако, и нечто принципиально новое, что следует из эйнштейновской трактовки тяготения. В первую очередь здесь нужно отметить вывод о конечности скорости распространения гравитации.

В ньютоновском законе всемирного тяготения о времени передачи взаимодействия ничего не говорится. Неявно предполагается, что оно осуществляется мгновенно, какими бы большими ни были расстояния между взаимодействующими телами. Такой взгляд вообще типичен для сторонников действия на расстоянии. Из теории Эйнштейна вытекает, что тяготение передается от одного тела к другому с такой же скоростью, что и световой сигнал. Если какое-то тело сдвигается с места, то вызванное им искривление пространства и времени меняется не мгновенно. Сначала это скажется в непосредственной близости от тела, потом изменение будет захватывать все более и более далекие области, и наконец во всем пространстве установится новое распределение кривизны, отвечающее измененному положению тела.

И вот здесь мы подходим к проблеме, которая вызывала и продолжает вызывать наибольшее число споров и разногласий - проблеме гравитационного излучения.

Может ли существовать тяготение, если нет создающей его массы? Согласно ньютоновскому закону - безусловно нет. Там такой вопрос бессмысленно даже ставить. Однако, как только мы согласились, что гравитационные сигналы передаются хотя и с очень большой, но все же не бесконечной скоростью, все радикально меняется. Действительно, представьте себе, что сначала вызывающая тяготение масса, например шарик, покоилась. На все тела вокруг шарика будут действовать обычные ньютоновские силы. А теперь с огромной скоростью удалим шарик с первоначального места. В первый момент окружающие тела этого не почувствуют. Ведь гравитационные силы не меняются мгновенно. Нужно время, чтобы изменения в кривизне пространства успели распространиться во все стороны. Значит, окружающие тела некоторое время будут испытывать прежнее воздействие шарика, когда самого шарика уже нет (во всяком случае на прежнем месте).

Получается так, что искривления пространства^* обретают определенную самостоятельность, что можно вырвать тело из той области пространства, где оно вызывало искривления, причем так, что сами эти искривления, хотя бы на больших расстояниях, останутся и будут развиваться по своим внутренним законам. Вот вам и тяготение без тяготеющей массы! Можно пойти и дальше. Если заставить наш шарик колебаться, то, как получается из эйнштейновской теории, на ньютоновскую картину тяготения накладывается своеобразная рябь - волны тяготения. Чтобы лучше представить себе эти волны, вернемся опять к нашей модели - резиновой пленке. Если не только нажать пальцем на эту пленку, но одновременно совершать им колебательные движения, то эти колебания начнут передаваться по растянутой пленке во все стороны. Это и есть аналог гравитационных волн. Чем дальше от источника, тем такие волны слабее.

^*(Точнее, везде нужно говорить об искривлении пространства - времени.)

А теперь в какой-то момент перестанем давить на пленку. Волны не исчезнут. Они будут существовать и самостоятельно, разлетаясь по пленке все дальше и дальше, вызывая на своем пути искривление геометрии.

Совершенно так же волны искривления пространства - гравитационные волны - могут существовать самостоятельно. Такой вывод из теории Эйнштейна делают многие исследователи. Но эти исследователи идут и дальше. Гравитационные волны могут не только излучаться, - говорят они, - но также и поглощаться, подобно всем другим волнам. Конечно, все эти эффекты очень слабы. Так, например, энергия, выделяющаяся при сгорании одной спички, во много раз больше энергии гравитационных волн, излучаемых всей нашей солнечной системой за то же время. Но здесь важна не количественная, а принципиальная сторона дела.

Существуют ли гравитационные волны?

Как только произнесены слова "энергия гравитационных волна", нужно остановиться и подумать: а что является носителем этой энергии? Ясно, что гравитационные волны, - ответит читатель. Это видно из самого названия. Но ведь, согласно всем нашим предыдущим рассуждениям, гравитационные волны - это "волны кривизны пространства"! Может ли иметь "кривизна пространства" какую-то энергию! Ведь искривляется не какой-то упругий стержень - там, понятно, нужно затратить работу на деформацию. Наши же искривления - это просто отступления от евклидовости пространства. Причем, заметьте, пустого пространства.

Положение усложняется еще и тем, что в любой точке пространства можно убрать тяготение, перейдя в соответствующую систему отсчета "падающего лифта", о котором уже рассказывалось раньше. Можно ли при этом говорить, что искривленное пространство имеет запас энергии, если само искривление в одной системе существует, а в другой - нет!

Можно, - отвечают сторонники гравитационных волн. Ведь система "падающего лифта" "выпрямляет" пространство, выключает тяготение отнюдь не сразу повсеместно. Если это тяготение снимается в одной точке, то в других оно при этом, наоборот, растет. Нельзя подобрать такую систему отсчета, движущуюся с ускорением, которая бы была эквивалентна, например, всему распределению земного тяготения. Если падающий лифт поместить над северным полюсом, то это значит, что перестает чувствоваться сила притяжения именно над этим полюсом, но в этой же системе силы притяжения над южным полюсом должны, наоборот, удвоиться. Точно так же и в гравитационной волне выбор системы отсчета влияет лишь на перераспределение энергии в пространстве, но ни в коем случае не означает возможности по нашему произволу получать либо нулевую, либо отличную от нуля энергию.

Сторонники гравитационных волн - а они, по- видимому, сейчас в большинстве - предсказывают и еще одно удивительное явление: превращение гравитации в такие частицы, как электроны и позитроны (они должны рождаться парами), протоны и антипротоны и т. д. (Иваненко, Уиллер и др.).

Выглядеть это должно примерно так. До некоторого участка пространства дошла волна тяготения. В определенный момент это тяготение резко, скачком, уменьшается и одновременно там же появляется, скажем, электронно-позитронная пара. То же можно описать и как скачкообразное уменьшение кривизны пространства с одновременным рождением пары.

Есть много попыток перевести это на квантово- механический язык. Вводятся в рассмотрение частицы - гравитоны, которые сопоставляются неквантовому образу гравитационной волны. В физической литературе имеет хождение термин "трансмутация гравитонов в другие частицы", причем эти трансмутации - взаимные превращения - возможны между гравитонами и любыми, в принципе, частицами. Ведь не существует частиц, нечувствительных к гравитации.

Пусть такие превращения маловероятны, т. е. случаются чрезвычайно редко, - в космических масштабах они могут оказаться принципиальными.

Пока, впрочем, не известно, имеют ли вообще место эти явления в действительности.

Новые возможности

Любопытно отметить, что сейчас усиленно обсуждается вопрос о возможности технического использования гравитационных волн, и может быть мы станем свидетелями появления гравиоприемников и гравиопередатчиков. Такого рода связь будет обладать важным преимуществом. Гравитационные волны могут проходить почти не поглощаясь сквозь любые вещества, тогда как, например, электромагнитные волны сквозь электропроводящие среды (в том числе землю и морскую воду) практически не проникают. Правда, пока еще не решено множество проблем. Достаточно сказать, что не только передать гравиограмму, но даже просто убедиться на опыте в конечности скорости распространения тяготения пока еще не удалось. Слишком уж малы здесь эффекты: гравитационные силы очень слабы. Однако работы в этом направлении интенсивно ведутся как в советских, так и в зарубежных лабораториях.

Конечная, но безграничная Вселенная

Выше в связи с обсуждением гравитационных трансмутаций частиц мы упомянули о космологии. И здесь нельзя не отметить, что эйнштейновская теория оказалась необычайно стимулирующей для развития именно космологических представлений. Толчок, который она дала, вызвал к жизни совершенно небывалые дотоле идеи и буквально обновил древнейшую из наук о природе - космологию.

Вселенная

Вселенная... Что мы знаем о ней? Ведь наши приборы позволят нам заглянуть только в крохотный "уголок" Вселенной. Неисчислимые мириады звезд находятся так далеко от Земли, что наши оптические и радиотелескопы не могут "дотянуться" до них. Но мысль зовет исследователей все дальше. А что находится там, за чертой исследованного? Основанные "на общих соображениях" догадки, что "там" все идет до бесконечности по принципу "и так далее", действовали, в общем, успокоительно и не слишком подталкивали фантазию. Но вот в 1917 году будто шквал пронесся в научном мире. Эйнштейн выступил с теорией конечной Вселенной. "Конечная Вселенная! Значит, существует какая-то граница Вселенной? А что там, по ту сторону границы? Что же, там "кончается пространство"? Разве мыслимо, чтобы...?"

Впрочем, прервем поток вопросов, многие из которых действительно обрушились на физиков. Попробуем разобраться, в чем, собственно, состоит утверждение о конечности пространства. И здесь нам опять поможет наша модель - пленка с ее "двумерными обитателями", которую мы ввели в свое время для пояснения кривизны пространства. Мы молчаливо предполагали раньше, что эта пленка простирается вширь неограниченно далеко и лишь местами изгибается там, где находится "материя", т. е. создающие гравитацию тела. "Мир" в нашей модели был бесконечным. Ну, а если эта "материя" распределена более или менее равномерно? Тогда кривизна - тоже примерно одинаковая - должна быть везде. Как же представить себе такую пленку, которая везде искривлена одинаково? Нет ничего легче, достаточно вспомнить обычный детский воздушный шарик!

И вот попытаемся опять "войти в положение" тех двумерных исследователей, которыми наша фантазия населила пленку. Для них поверхность шара - это все пространство. Действительно, если бы они снарядили экспедицию, дав ей строгий наказ двигаться все время в одну и ту же сторону - "по прямой" (мы взяли последние слова в кавычки, чтобы напомнить - сама "прямая" искривляется!), то эта экспедиция рано или поздно, к изумлению организаторов и участников, вернулась бы к исходной точке, только с другой стороны. Все новые и новые экспедиции могли бы отправляться в путь. И в какую бы сторону они ни направлялись, все они должны были бы, совершив замкнутый круг, возвращаться к месту отправления. Какой же вывод должны были бы сделать двумерные мужи науки? Единственный: "Наша Вселенная,- сказали бы они, - не простирается до бесконечности, а имеет конечные размеры. Но в то же время она безгранична - ни одна из экспедиций не обнаружила ничего похожего на границу Вселенной". Безграничная, но не бесконечная! Именно такими словами определил Эйнштейн в своей теории наше пространство. Смысл этих слов в общем тот же, что и в модели: если представить себе летящий все прямо и прямо космический корабль, то он должен в конце концов вернуться к месту старта (если, разумеется, ему не помешает столкновение с небесными телами). Но можно говорить и не о космическом корабле - то же произойдет и с самым быстрым из путешественников - со световым лучом. Двигаясь в искривленном тяготением пространстве, он "замкнется на себя", пролетев сквозь неоглядные дали безграничного, но все же конечного пространства.

Расширяющаяся Вселенная

Однако это еще не все: теория гравитации Эйнштейна не только дает возможность говорить о конечности Вселенной, но приводит к еще более поразительному выводу - выводу о расширении Вселенной.

Впервые этот вывод, к которому сам Эйнштейн вначале отнесся скептически, был сделан советским физиком А. Фридманом.

В основе теории Фридмана лежит следующее основное предположение: Вселенная в целом однородна и изотропна. Это означает, что ни один из больших участков Вселенной не отличается по своим свойствам от остальных. Все направления во Вселенной совершенно равноправны. Средняя плотность вещества всюду одинакова.

При этом предположении уравнения тяготения Эйнштейна, совершенно однозначно приводят к выводу о том, что Вселенная не может быть стационарной. Она расширяется, так что все звездные скопления - галактики - разбегаются друг от друга.

Вспомним нашу двумерную модель конечной Вселенной - детский шарик. Этот шарик - Вселенная - непрерывно раздувается, так что расстояния между любыми его точками возрастают. Причем возрастают тем быстрее, чем дальше эти точки расположены друг от друга: ведь увеличивается каждый сантиметр отрезка кривой, соединяющей точки. Двумерные астрономы наверняка смогли бы это обнаружить.

Если смотреть на удаляющуюся звезду, то ее спектр будет смещаться в сторону длинных волн. Все линии делаются "более красными". (Это явление называется красным смещением, а вызвано оно эффектом Доплера; смещение тем заметнее, чем больше скорость.)

Самое замечательное в том, что наши земные астрономы сумели обнаружить такое явление. Американский астроном Хаббл установил, что все звездные острова Вселенной - галактики - удаляются от нашей. Причем, чем дальше от нас галактика, тем больше смещаются спектральные линии ее световых волн, тем больше, следовательно, относительная скорость движения галактик. Эта скорость u удовлетворяет простому закону: u = Нr, где r - расстояние до галактики, а Н - постоянная Хаббла.

Наиболее удаленные галактики убегают от нашей с фантастическими скоростями порядка 100 000 км/сек, т. е. около одной трети скорости света. При этом сине-зеленый свет галактик воспринимается нами как красный.

Закон Хаббла непосредственно вытекает из теории Фридмана. Причем Н убывает обратно пропорционально времени и, следовательно, скорость расширения Вселенной должна уменьшаться.

Поразительное теоретическое предсказание сомкнулось с замечательным экспериментальным открытием. Не удивительно, что научный мир - да и не только он - был буквально потрясен новизной и смелостью космологических идей Эйнштейна - Фридмана. Слово "переворот" безо всяких скидок подходит к тому, что здесь произошло.

Прошедшее и будущее Вселенной

То, что Вселенная расширяется (или, точнее, тот участок Вселенной, в котором мы живем,) - совершенно бесспорно. Это непосредственный экспериментальный факт. К этому же приводит теория. Но что будет с Вселенной в дальнейшем? Какова она была в прошлом? Наконец, конечна или бесконечна Вселенная в действительности?

Определенных ответов на эти вопросы нет, но многое можно сказать уже сейчас, если допустить справедливость предположения об однородности и изотропности Вселенной.

Поговорим сначала о будущем Вселенной. Как ни странно, именно здесь есть большая определенность. Имеется лишь две возможности, и речь идет о выборе между ними.

Согласно теории все зависит от соотношения между средней плотностью Вселенной в данной момент времени р и некоторой критической плотностью 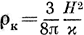, где Н - постоянная Хаббла в данный момент времени, а x - гравитационная постоянная^*.

^*(Фактически соотношение между ρ и ρ_к определяется отношением потенциальной и кинетической энергий Вселенной.)

Если ρ меньше ρ_к, то расширение Вселенной никогда не прекратится. Скорость разбегания галактик постепенно будет уменьшаться, но никогда расширение не сменится сжатием. Галактики разойдутся на невообразимые расстояния, и наш звездный остров окажется совершенно затерянным в безбрежном океане пространства.

Но если ρ больше ρ_к, то с течением времени расширение Вселенной сменится сжатием и место красного смещения займет фиолетовое. Когда это произойдет, если это вообще произойдет, предсказать пока нельзя.

Итак, чтобы знать будущее Вселенной, надо знать среднюю плотность материи внутри нее. Плотность ρ_к = 2·10^-29 г/см³ известна, так как постоянная Хаббла и гравитационная постоянная могут быть измерены достаточно точно.

Главная трудность в определении р. Надо знать массу материи (как вещества, так и излучения) не только в звездах, но и во всем межзвездном пространстве видимой части Вселенной. Оценки, которыми мы сейчас располагаем, весьма противоречивы. По одним данным ρ меньше ρ_к, а по другим больше. Окончательные выводы не получены.

Определение плотности материи играет важнейшую роль еще в одном отношении. Соотношение ρ и ρ_к, от которого зависит будущее Вселенной, является определяющим для пространственной структуры Вселенной как целого. При ρ, большем ρ_к, средняя кривизна мира положительна и Вселенная конечна. При ρ, меньшем ρ_к, Вселенная бесконечна. Значит, теория гравитации Эйнштейна показывает лишь, что наша старая уверенность в бесконечности Вселенной может и не соответствовать истине, но не утверждает безоговорочно, что мир замкнут в себе самом.

Посмотрим теперь, что можно сказать о прошлом мира. Когда-то Вселенная должна была быть сжата в очень малом объеме. Плотность материи в этот момент была бесконечно велика. Если принять этот момент за начало отсчета времени (t = 0), то, зная постоянную Хаббла, можно оценить время расширения Вселенной. Оно оказывается сравнительно невелико: всего лишь 10 миллиардов лет. Не много по астрономическим масштабам^*.

^*(Кстати, тот же порядок времени дают совершенно иные оценки, основанные на определении возраста минералов по радиоактивному распаду.)

В каком состоянии находилось вещество Вселенной в этот момент? Как из такого сверхплотного вещества возникла наша Вселенная с ее звездами и звездными скоплениями? И, наконец, что же было со Вселенной до этого?

На все эти вопросы никто сейчас не в состоянии дать определенного ответа. Однако и здесь уже намечаются возможные решения.

При сверхплотном состоянии вещества в начальном состоянии Вселенной, очевидно, не одна только гравитация должна быть существенной. Не меньшую роль должны были играть и другие силы. Поэтому лишь после знакомства с ними мы можем сказать несколько слов о существующих здесь гипотезах.

Сгущение материи в звезды и галактики по мере расширения Вселенной было вызвано, вероятно, гравитационной конденсацией, о которой мы говорили, обсуждая теорию Шмидта. В дальнейшем при эволюции звезд начали играть, несомненно, большую роль ядерные и другие силы наряду с гравитационными. Пока мы это тоже не будем обсуждать.

А вот что было со Вселенной до начала расширения? Если допустить, что Вселенная будет расширяться бесконечно, ответа на этот вопрос не видно вовсе^*.

^*(Правда, и здесь уже в последнее время появилась гипотеза Я. Зельдовича о рождении миров за счет столкновения элементарных частиц сверхгигантских энергий, блуждающих в бесконечных просторах Вселенной. Это - выход из тупика, хотя и довольно фантастический. Приняв такую гипотезу, вряд ли можно исследовать Вселенную в глубь прошлого. Существование таких частиц надо рассматривать как изначальное.)

Проще, в принципе, дать ответ для конечной Вселенной. Ведь тогда расширение может вообще говоря смениться сжатием, и состояние Вселенной в момент t = 0 нужно рассматривать как результат предшествующего сжатия. Тогда мы придем к гипотезе пульсирующей Вселенной. Вселенная пульсирует (расширяется и сжимается) извечно с периодом, который пока знать нам не дано^*. На наш взгляд, это самая простая и наиболее доступная нашему разуму картина эволюции Вселенной, существующей вечно. Но, конечно, не критерий простоты должен быть в таких вопросах решающим.

^*(Надо сказать, что, вероятно, при пульсациях Вселенная не сжимается до бесконечной плотности. Скорее всего, Вселенная никогда не имела сколь угодно большой плотности.)

Великий шаг на пути познания природы

Может возникнуть желание спросить: если теория гравитации Эйнштейна так сложна, если космологические выводы из нее имеют в значительной степени предварительный, а зачастую и фантастический характер, если, наконец, эта теория не помогла сконструировать ни одной машины, ничем не обогатила пока технику, то что же тогда заставляет самых выдающихся современных ученых говорить о ней, как о "самом замечательном достижении человеческого ума"? Что привлекает к ней неослабное внимание физиков, философов, астрономов, да и огромное число мыслящих людей вот уже более сорока лет? Разумеется, не только "хороший вкус человечества". И не только могучая красота основных принципов этой теории.

Главное - это открытие необычайно сложных новых физических связей, о которых прежде исследователи природы даже не подозревали.

С помощью теории Эйнштейна мы вступили в новую область, представляющую для человека ни с чем не сравнимый интерес. Здесь впервые в точной физической теории мы приблизились к познанию бесконечного. Человек впервые начал ощущать дыхание Вселенной не с помощью поэтических откровений, а на путях точного знания. Без теории Эйнштейна большинство тех вопросов, о которых шла речь, не могли быть даже поставлены.

Примерно сто лет назад, обнаружив связь между световыми и магнитными явлениями, Фарадей в восторге писал, что ему "удалось намагнитить свет и осветить магнитную силовую линию".

Теория Эйнштейна, можно смело сказать, пролила новый свет на научное миропонимание, "магнетизм" ее идей властвовал и продолжает властвовать над естествоиспытателями. .

И как бы ни пошло дальнейшее развитие нашего понимания гравитации, гениальное творение "Ньютона двадцатого века" всегда будет покорять своей неповторимой дерзновенностью, всегда останется великим шагом на пути познания природы.