
2. Систематика элементарных частиц
Одна элементарная частица - "композиция" всех остальных
Открытие резонансов усложнило и без того простую картину мира. Вопрос о том, что такое элементарная частица, приобрел еще большую остроту. Ведь и так нельзя было с уверенностью утверждать, что все 35 частиц с относительно большими временами жизни (у некоторых оно бесконечно велико) являются элементарными. Слишком уж их много. Теперь к ним еще добавились резонансные частицы.
Но не только в этом дело. Сейчас становится бесспорным, что частицы, называемые по привычке элементарными, обладают в действительности крайне сложной структурой. Так, например, протоны и нейтроны окружены облаками пионов. Пионы структурно входят в нуклон. В свою очередь, π-мезоны могут превращаться в пару нуклон - антинуклон. Следовательно, нельзя разложить частицы по ящичкам и изучать изолированно каждую из них. Раскрытие образа одной какой-нибудь частицы невозможно без учета других. Каждая элементарная частица начинает, по выражению Маркова, представляться "композицией" всех остальных. Получается замкнутый круг: свойства одной из частиц определяются всеми остальными. Размыкается где-либо этот круг, т. е. имеются ли простейшие частицы, из которых построены все остальные, или же в природе не существует частиц такого рода?
Пока это неизвестно. Никакого критерия элементарности частицы у нас нет.
Можно надеяться, что открытие резонансов лишь временно усложнило картину мира. В дальнейшем их исследование поможет решить проблему внутренней структуры элементарных частиц - проблему, являющуюся проблемой № 1 в современной физике.
Именно в вопросе о резонансах, пожалуй, наиболее ярко проявилась необходимость внести новое в те методы теоретического описания, которые применялись доныне.
Проблески единства
Уже сейчас открытие резонансов помогло увидеть то, что оставалось до сих пор скрытым от взоров исследователей. Представьте себе, что перед вами большое полотно, скрытое за плотной завесой. Вы хотите узнать, что за ним, но не в силах отбросить всю завесу сразу. Вот вам удалось прорвать ее в одном, другом месте и кое-где стали видны отдельные фигурки. Теперь нет сомнения, что перед вами картина со многими действующими лицами, а не просто грунтованный кусок холста.
Еще усилие - и целые участки картины обнажены. На некоторых из них можно усмотреть глубокое родство между изображенными персонажами, единство композиции. Другие участки столь малы, что трудно понять, чем связаны их отдельные детали.

Резонанс
Гораздо труднее по случайным фрагментам догадаться, что общего между ними, уловить то целое, что изображено на картине, большая часть которой скрыта от вас.
Но вот постепенно завеса начинает спадать. Вы внимательно вглядываетесь в картину и обнаруживается удивительно цельный характер изображенного: отдельные фрагменты сливаются воедино. Больше того, вы можете даже догадаться, представить себе, что изображено на участках полотна, еще не доступных взору.
Картина не проста. Собственно, здесь целая серия картин, превосходящая числом классический триптих.
Приблизительно нечто подобное произошло в самое последнее время, когда творение Великого мастера - Природы - мир простейших частиц - предстало, после открытия резонансов, перед учеными в более обнаженном виде, чем когда-либо.
Близнецы в электрической одежде
Когда физики только начинали знакомиться с элементарными частицами, каждая из них казалась яркой и обособленной индивидуальностью. Но число известных частиц росло и они как-то почти сами собой начали разбиваться на группы, внутри каждой из которых обозначались признаки определенного родства.
Началась классификация частиц.
По каким же признакам можно проводить систематику?
Исторически первым признаком была масса. (Вероятно, здесь не последнюю роль сыграл поразительный пример менделеевской классификации элементов.) Частицы были разделены на группы - их так и называли тогда: легкие, средние и тяжелые. Однако эта схема потребовала уточнений. Пришлось учитывать спин и - что для нас особенно важно - характер взаимодействия. Так родились известные классы частиц: лептоны, мезоны*, тяжелые частицы - барионы и, наконец, к ним добавились резонансы. Лишь фотон был и остается в одиночестве. Он сам образует целый класс**. С этой классификацией мы уже знакомились, разбирая таблицу элементарных частиц.
*(Своей большой массой -мезон ввел ученых в заблуждение и был сначала причислен к мезонам. Теперь стало ясно, что по своей природе он - лептон.)
**(Делались попытки установить его родство с нейтрино, но безуспешно.)
Но вот что любопытно. Если присмотреться повнимательнее к этой таблице, легко обнаружить среди мезонов и барионов группы частиц, которые прямо- таки напрашиваются на то, чтобы образовать из них четкие подгруппы.
Вот, например, три π-мезона: π+, π- и π0. Если бы не заряды, то как можно было бы их различить? По отношению к сильным взаимодействиям все они ведут себя абсолютно одинаково. У них одинаковый спин. Даже небольшое различие в массах - и то имеет электромагнитное происхождение: исчезни электрические заряды - и массы стали бы одинаковыми. Как тут удержаться и не сказать, что три π-мезона - это, в сущности, не разные частицы, а одна, но только в различных зарядовых состояниях!
π-мезоны - не единственный известный нам пример близнецов, отличающихся лишь электрическими одеждами. Как, вероятно, помнит читатель, разговор о ядерных силах привел нас к такому же выводу относительно протона и нейтрона. Можно вообще сказать, что это не какой-то особый случай, а правило. Мимо него нельзя пройти, не насторожившись.
Познакомимся поближе с зарядовыми мультипле- тами (так стали называть группы частиц, отличающихся только зарядовыми состояниями). Кроме триплета (мультиплета из трех частиц) π-мезонов существует еще триплет Σ-гиперонов. К-мезоны, как и протон с нейтроном, образуют зарядовый дублет (2 частицы); Λ0-гиперон - синглет, т. е. единственный представитель особого зарядового мультиплета.
Близнецами в "электрической одежде" оказались и резонансы. Так, наряду с резонансом N*++, возникающим при рассеянии π+-мезонов на протонах, имеются еще пион-нуклонные резонансы N*+, N*-, различающиеся только электрическими зарядами. Эти заряды равны соответственно 2е, е, 0 и -е.
Принадлежность к определенному зарядовому мультиплету и число частиц в этом мультиплете - это важнейшая отметка в паспорте элементарной частицы. Однако оказывается, что гораздо удобнее говорить не о числе частиц в мультиплете, а о так называемом изотопическом спине и о проекциях изотопического спина.
Что такое изотопический спин?
Самый термин "изотопический спин" представляет собой соединение понятий, каждое из которых порознь нам уже встречалось. Изотопами, как вы помните, называются элементы- близнецы, которые не различаются по своим химическим свойствам, но могут иметь несколько отличные физические "параметры" - массу, например.
В таблице Менделеева все изотопы стоят в одной клетке и все они имеют одно и то же наименование. Мы говорим, например, что гелий-три (Не3) и гелий-четыре (Не4) - это не разные элементы, а, если хотите, разные состояния одного и того же элемента. Подобно этому все частицы - члены одной семьи зарядового мультиплета - также рассматриваются как одна частица, но только находящаяся в различных состояниях.
Ну, а при чем здесь "спин"? Если иметь в виду тот спин, который мы обсуждали в главе без номера и который можно определить как "собственный вращательный момент", то совершенно не при чем. И если одно и то же слово употребляется в совершенно разных смыслах, то здесь нет ничего ни нового, ни удивительного. Мало ли таких примеров? Сила ветра измеряется в баллах. В баллах же оцениваются знания учащихся. Слово "градус" вполне успешно "работает" и при рассказе о температуре, и для измерения углов. Те же углы можно измерять в минутах и секундах, являющихся в то же время мерой совсем другой величины - времени. Впрочем, этот последний пример заслуживает того, чтобы на нем остановиться. Стрелка секундомера бежит по циферблату. Если полный оборот - один час, то изменение угла за одну минуту (минуту времени!) точно равно одной "угловой" минуте. Здесь полный параллелизм - он, конечно, связан с выбором той "механической модели", которую мы применяем для измерения времени (например, взяв песочные часы, мы бы ничего подобного не получили).
А теперь выберем другую "механическую модель" - частицу с определенным спином. Пусть этот спин равен, например, 1/2 (все, напоминаем, в единицах 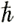 ). Такая частица, как вы помните, может иметь всего две ориентации - либо ее спин параллелен импульсу, либо антипараллелен. Две ориентации, два возможных состояния. А если спин равен нулю, то, разумеется, "как ни верти" частицу, ничто не изменится - значит, здесь всего одно состояние.
). Такая частица, как вы помните, может иметь всего две ориентации - либо ее спин параллелен импульсу, либо антипараллелен. Две ориентации, два возможных состояния. А если спин равен нулю, то, разумеется, "как ни верти" частицу, ничто не изменится - значит, здесь всего одно состояние.
А спин, равный 1? Квантовый подсчет говорит, что здесь возможны три различных состояния. Если спин частицы 3/2, то таких состояний четыре, и т. д. В общем случае спин, равный n, обеспечивает возможность 2n+1 различных "внутренних", как их называют, состояний. А теперь вспомним о наших "семействах" частиц. Напомним, что "членов каждого из этих семейств" мы рассматриваем опять как одну частицу, но в различных "внутренних" состояниях. И число таких состояний от "семейства" к "семейству" меняется. У самых бедных (Λ0-гиперон) - всего одно. (Как не вспомнить о нулевом спине!) У других (нуклоны) их два. Опять полная аналогия со случаем спина 1/2. У π-мезонов (π+, π0 и π-) три, как для спина, равного единице, и т. д. Теперь вы видите, что наша "механическая модель" вполне себя оправдывает, а, стало быть, есть все основания говорить об изотопическом спине.
Но мы можем сделать и еще один шаг: вспомним, что, в то время как значение спина (мы опять говорим о "механическом спине") показывает число возможных внутренних состояний, конкретное задание каждого из этих состояний можно производить, например, указывая, как направлен спин (по отношению к импульсу или вообще любой оси; по традиции обычно выбирают ось z); то же самое можно выразить и в такой форме: состояние определяется проекцией спина на ось z. Ничто не мешает нам поступать аналогично и в случае изотопического спина - приписывать каждому из членов наших "изоспиновых семейств" определенное значение "проекции изотопического спина на ось z". Конечно, можно было бы и просто указывать заряд. Ведь из предыдущего явствует, что эта проекция как раз и определяет заряд частицы семейства, но, оказывается, именно проекция изотопического спина является наиболее удобной величиной для математического аппарата теории.
Заряд
Дело, однако, не только и не столько в удобстве. Изотопический спин обладает одним необычайно важным свойством, которое само по себе выдвигает его на почетное место: при сильных взаимодействиях изоспин сохраняется. Это значит, что при любых превращениях, обусловленных сильными взаимодействиями, суммарное значение изоспина всех частиц до превращения такое же, как у частиц, образовавшихся после превращения. Так, например, в реакции
р + π- → n + π0
изотопический спин начальных частиц равен 3/2 (1/2 у протока и 1 у π--мезона). Частицы в конечном состоянии имеют суммарный изоспин, равный также 3/2 у n и 1 у π0-мезона).
Закон сохранения изотопического спина при сильных взаимодействиях является концентрированным выражением независимости сильных взаимодействий от электрического заряда. Это единственный закон сохранения, выполняющийся только при сильных взаимодействиях.
| Частица | Число частиц в мультиплете | Изотопический спин | Заряд частицы | Проекция изотопического спина |
|---|---|---|---|---|
| Λ0 | 0 | 0 | 0 | 0 |
| р | 2 | 1/2 | +е | +1/2 |
| n | 2 | 1/2 | 0 | -1/2 |
| π+ | 3 | 1 | +е | +1 |
| π0 | 3 | 1 | 0 | 0 |
| π- | 3 | 1 | -е | -1 |
| К+ | 2 | 1/2 | +е | +1/2 |
| К0 | 2 | 1/2 | 0 | -1/2 |
| Σ+ | 3 | 1 | +е | +1 |
| Σ0 | 3 | 1 | 0 | 0 |
| Σ- | 3 | 1 | -е | -1 |
| N*++ | 4 | 3/2 | +2e | +3/2 |
| N*+ | 4 | 3/2 | +e | +1/2 |
| N*0 | 4 | 3/2 | 0 | -1/2 |
| N*- | 4 | 3/2 | -e | -3/2 |
В таблице приведено несколько примеров соответствия между числом частиц в зарядовом мультиплете и зарядами частиц, с одной стороны, и изотопическим спином наряду с его проекциями, с другой.
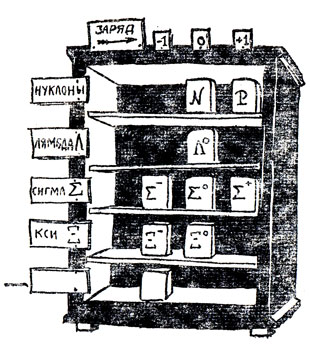
Впрочем, показ всегда нагляднее, чем рассказ. Представим себе, что мы производим систематику частиц, барионов например, т. е. раскладываем их по полочкам не в переносном, а в самом буквальном смысле этого слова. Мы даже нарисуем эти полочки, для каждого зарядового мультиплета по одной, и отведем места для частиц в строгом соответствии с их зарядами.
Теперь, когда частицы разложены по полочкам, можно полюбоваться делом своих рук. Но вот что странно - расположение оказалось каким-то несимметричным. Эту асимметрию можно описать количественно; достаточно определить средний заряд на каждой полочке. Для нуклонов - они самые старые наши знакомые из семьи барионов - этот средний заряд мультиплета равен +1/2. С этим значением мы и будем сравнивать средние заряды всех остальных барионных мультиплетов (чтобы получались целые, а не дробные значения, удобно брать удвоенную разность средних зарядов мультиплетов). Вот, например, Ξ-частицы. Средний заряд равен -1/2. Удвоенная разность этого и нуклонного среднего заряда равна -2. Для Σ-триплета получаем тем же способом значение -1, как и для Λ0. Нетрудно проделать аналогичные подсчеты и для мезонов, приняв за "эталон" (т. е. считая для них смещение равным нулю) π-мезоны. Не напоминают ли вам что-либо получившиеся цифры? Ну, конечно, это же значения странностей, которые играли такую важную роль в рассказе о слабых взаимодействиях.
Очень любопытно! С новой точки зрения, интересуясь систематикой частиц (мы ведь не думаем сейчас ни о каких распадах или иных взаимных превращениях), мы опять пришли к необходимости ввести в рассмотрение странность.
Кирпичики в кирпичиках
Поставив перед собой задачу - навести порядок среди становящейся все более обширной коллекции частиц (даже заведя с этой целью шкафы), мы выделили среди других четыре признака: спин, массу, заряд и странность. Спин определяет, в какой из шкафов - барионный или мезонный следует помещать частицу (лептоны мы рассматривать не будем), а остальные величины указывают номер соответствующей полки и место на ней.
Все чинно и аккуратно, порядок наведен, систематика есть! Но какой от нее прок? Имеет ли она хоть какой-либо физический смысл? Правильно ли выбраны признаки, по которым произведена классификация? Представьте себе, что мы занимались бы не классификацией частиц, а систематикой в биологии и взяли бы за основу, скажем, вес животного. Могло бы оказаться, что ближайшими родственниками человека, к примеру, являются крокодил и свинья. Дело, конечно, не в том, насколько это лестно для нас, людей, - такая систематика просто не способствует углублению понимания животного мира. Итак, хороша ли наша классификация элементарных частиц?
Прежде всего отметим, что все выбранные нами признаки - это величины, не меняющиеся при сильных взаимодействиях. При любых превращениях, вызванных этими взаимодействиями, электрический заряд исходных "продуктов" и тех, которые образуются в конечном состоянии, одинаков. То же можно сказать о странности и о спине. (Анализ положения с массой сложнее, и мы здесь этого касаться не будем.)
Может сложиться такое впечатление, что есть ка- кой-то набор материальных носителей заряда, странности и спина, какие-то субчастицы, которые, склеиваясь в определенных комбинациях, формируют ба- рионы и мезоны, причем во всех превращениях сами эти субчастицы не исчезают и не возникают, а только переходят из одних комбинаций в другие. Если поверить в это, то сохранение заряда или странности выглядит не более удивительным, чем сохранение числа деталей в детском конструкторе, независимо от того, сделан ли из этих деталей паровоз или мельница.
Элементарные частицы уже давно поэтически называют кирпичиками материи. Но если существуют субчастицы, то, стало быть, эти кирпичики состоят из других кирпичиков, "еще более элементарных"? Эта идея столь соблазнительна, что нельзя отказать себе в удовольствии поговорить о ней подробнее.
Кварки?
Прежде всего заметим, что у наших субчастиц должен быть спин, равный 1/2. Действительно, из половинок можно составить как целые, так и полуцелые спины, чего мы не могли бы сделать, будь в нашем распоряжении только "детали" со спином, равным нулю, единице или любому целому числу.
Ну, а заряд, масса, странность?
Вот здесь нас подстерегает сюрприз. Оказалось, что наиболее цельная картина получается, если, отказавшись от прочно укоренившейся привычки, приписать нашим кирпичикам в кирпичиках не целочисленные (т. е. кратные электронному), а дробные заряды.
Дробные заряды! Еще недавно такая идея показалась бы бредовой. Однако именно три такие частицы ввел в рассмотрение Гелл-Манн. Он же дал им название "кварки". О происхождении этого названия хорошо написали в журнале "Знание - сила" М. Карев и В. Владимиров: "Оказывается, виноват... Финнеган, герой романа английского писателя Джойса... Финнегану - или его двойнику, "вытеснившему его из жизни", мерещится, что он король Марк из средневековой легенды, у которого племянник Тристан похитил жену Изольду. Король Марк гонится за Изольдой на корабле, над ним кружатся чайки (которые, впрочем, может быть вовсе не чайки, а судьи) и злобно кричат: "Три кварка мистеру Марку", и все громче их загадочный, страшный клич: "Три кварка, три кварка, три кварка". Короче говоря, термин "кварки" "в переводе" на нормальный человеческий язык должен обозначать нечто вроде "бредовые", "немыслимые", "кошмарные", "дикие" - можете смело продолжить список синонимов.
Сколько же нужно ввести кварков? Разумеется, хотелось бы как можно меньше. Оказывается, необходимый минимум - три кварка. В литературе они часто обозначаются малыми буквами р, n и λ, (не путать с символами протона, нейтрона и лямбда-частицы, которые в дальнейшем обозначаются Р, N и Λ).
Спины всех кварков будем, как уже договорились, считать равными 1/2, а остальные свойства удобно представить в виде такой таблицы:
| Символ кварки | Электрический заряд | Странность | Барионный заряд |
|---|---|---|---|
| р | +2/3 | 0 | 1/3 |
| n | -1/3 | 0 | 1/3 |
| λ | -1/3 | -1 | 1/3 |
Попробуем теперь комбинировать кварки таким образом, чтобы получать известные нам частицы. Начнем, скажем, с протона Р. Странность протона равна О, следовательно, мы должны ограничиваться набором из р и п. Всего в Р должны входить три кварка, чтобы общее барионное число получилось равным единице. Если учесть к тому же, что заряд Р равен +1, то мы приходим к единственному набору: ррп. Впрочем, нет, не единственному. Мы забыли о спине. Необходимо позаботиться о том, чтобы суммарный спин был равен 1/2. Этого можно добиться, если принять, что спины двух р-кварков параллельны, а спин n антипараллелек им (или "оси Z", как говорят физики, т. е. какому-то выбранному направлению в пространстве).
Символически это можно записать так:
Р = р ↑ р ↑ n↓.
Стрелка справа от символа обозначает направление его спина.
Рецепт образования частиц из кварков, вероятно, прояснился на этом примере и не производит впечатления сложного. Давайте же попробуем комбинировать тройки кварков и посмотрим, что из этого получится.
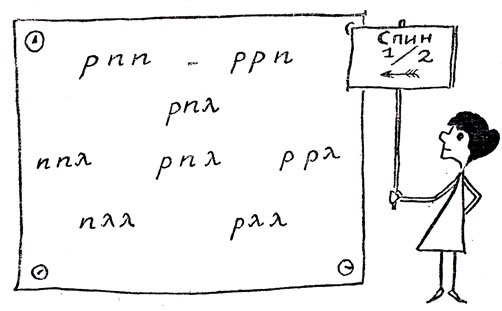
Скачала договоримся рассматривать такие комбинации, спин которых равен 1/2. Это значит, что спины всех кварков не могут быть направлены одинаково. Более тонкий анализ, опирающийся на принцип Паули, о котором мы уже раньше говорили в этой книге, показывает, что не все комбинации спинов являются "разрешенными". Например, если общий спин равен 1/2, то нужно исключить из рассмотрения комбинации из трех одинаковых кварков. Есть и ряд других тонких моментов, в обсуждение которых мы входить не будем. Давайте просто выпишем все "разрешенные" комбинации, располагая их рядами. Пусть внутри каждого ряда электрический заряд возрастает слева направо, а странность остается одной и той же в каждом ряду и уменьшается на единицу при переходе от каждого ряда к другому, расположенному под ним.
Мы получим такую таблицу*:
*(То, что у нас получились две (различные!) комбинации рnλ, связано с возможностью различных ориентаций спинов в этой тройке. Принцип Паули запрещает двум частицам одного сорта находиться в одинаковых состояниях. Однако в данном случае все кварки различны; значит, принцип Паули не вносит никаких запретов.
Выберем за направление "оси Z" направление р. Это даст нам возможность около первого, скажем, символа в нашей тройке писать стрелку, направленную вверх: p↑. Остается перебрать все возможные комбинации, дающие общий спин 1/2. Совершенно ясно, что таких комбинаций всего две: p ↑n↑λ ↓ и p↑n ↓λ↑. Это и поясняет, почему в нашей таблице рnλ появилось два раза.)
Cпин 1/2
Попробуем теперь сопоставить этим тройкам частицы. Комбинация ррn нам уже знакома - это протон. Легко видеть, что нейтрону соответствует ррn. Значит, первая строчка - это наклонный дублет. Зарядовый синглет рnλ можно сопоставить Λ0-частице; третья строчка дает триплет Σ-, Σ0, Σ+ и, наконец, в последней строке расположились комбинации кварков, которые по значению странности и электрическим зарядам точно соответствует Ξ-дублету.
Получается - и хорошо получается! Мы уже построили так называемый барионный октет - сверх- или супермультиплет, объединяющий все барионы в одну группу.
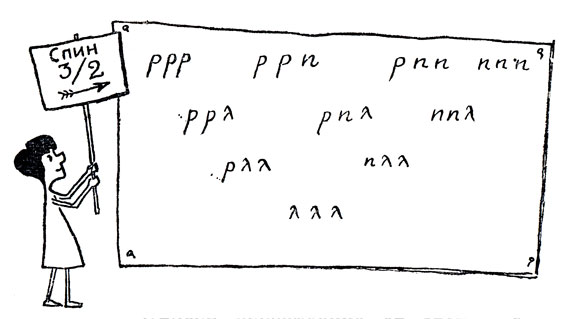
Давайте продолжим наше увлекательное комбинирование - нечто вроде варианта детских кубиков. переберем теперь тройки кварков с общим спином 3/2. И опять, придерживаясь тех же правил, что и в предыдущем случае, построим следующую таблицу.
Спин 3/2
Первое впечатление от этой таблицы такое, что мы понастроили частиц, которых и в природе-то нет. Например, что это за частица ррр? Ее электрический заряд должен быть равен +2, а ни у протона, ни у Σ, ни у Ξ заряд не превосходит единицы. А резонансы? Мы забыли о резонансах, - а ведь их тоже нужно включать в общую схему классификации. Среди резонансов есть нужная частица - это известный первенец семейства резонансов: N*++. Нашлось место для него в нашей систематике. Найдется место и для других резонансов. Без лишних слов выпишем соответствующую таблицу:
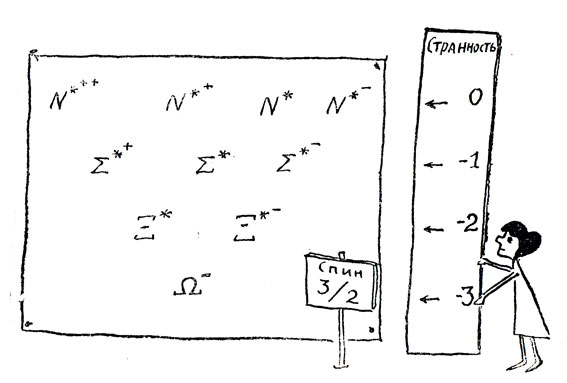
Странность спина
Предсказанная встреча
В этой таблице все уже довольно хорошо нам знакомо. Звездочки показывают, что мы имеем дело с резонансами, являющимися возбужденными состояниями частиц с соответствующими символами; стоящие около этой звездочки крестики или черточки определяют электрический заряд. Однако есть в таблице и нечто новое: символ Ω-. Раньше мы с ним не встречались. Что это такое? Не только мы не встречались раньше с такой частицей. Немногим более восьми лет назад о ней невозможно было узнать из самых полных обзоров. Лишь энтузиасты-теоретики, твердо уверовавшие в новую систематику, говорили: должна быть такая частица, ее нужно искать. Они даже подробно описывали эту частицу: у нее должен быть заряд -1, странность -3, барионное число +1, спин, равный 3/2. Более того, даже масса была предсказана теоретически. Как? Очень просто (задним числом все всегда очень просто).
Если, заглянув в таблицу резонансов, выписать оттуда массы, то нетрудно заметить, что у нас в таблице эти массы оказываются тем больше, чем ниже ряд. В то же время переход к каждому следующему ряду снизу сопровождается добавлением одного λ-кварка. В верхнем ряду λ нет, в следующем - одно λ, ниже - два и, наконец, Ω- состоит из трех λ-кварков. Сопоставив рост массы с ростом числа кварков, нетрудно сделать напрашивающийся вывод, что р- и n-кварки (им мы припишем одинаковые массы) легче, чем λ-кварк. Можно даже прикинуть, насколько. Достаточно сравнить массы резонансов в соседних рядах. Разница получается примерно в 0,16 массы нуклона (или в принятых теперь энергетических единицах 146 Мэв). Таким образом, Ω- должна иметь массу на 146 Мэв большую, чем Ξ*. Смотрим опять в таблицу. Масса Ξ* равна 1530 Мэв. Следовательно, Ω- должна иметь массу 1676 Мэв. Так предсказывали теоретики.
И вот 31 января 1964 года такая частица была экспериментально найдена! В Брукхейвенской лаборатории в США проводилось исследование столкновений К--частиц с протонами. Ω--частица была обнаружена в реакции:
K- + P → Ω- + K+ + K0.
Спустя примерно 10-8 секунд после своего рождения Ω- распадается по схеме: Ω- → Ξ0 + π-. Относительно большое время лсизни связано с тем, что распад по "сильным каналам", т. е. обусловленный сильными взаимодействиями, запрещен сохранением странности; изменение же странности, как мы говорили, возможно лишь при распадах за счет слабого взаимодействия.
Открытие Ω--частицы, поразительная точность, с которой подтвердились предсказания теории, не могли, конечно, не произвести сильнейшего впечатления. Если до этого систематика нередко рассматривалась как красивая, остроумная, но далекая от убедительности игра фантазии, то с обнаружением настроения физиков резко изменились. В воздухе явственно запахло большими событиями.
Множатся успехи...
Новая классификация приносила один успех за другим. Естественно и непринужденно вписались в общую систему мезоны и бозонные резонансы. Бозоны - частицы с целым спином. Следовательно, их нужно склеивать из четного числа кварков. Точнее, из равного числа кварков и антикварков* - ведь мы сейчас хотим получать частицы с барионным зарядом, равным нулю. (У всех антикварков барионный заряд, как и остальные квантовые числа, противоположен по знаку заряду соответствующих кварков.)
*(Антикварки обозначаются символами с чертой над ними.)
Наиболее простые комбинации такого сорта имеют вид: р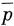 , n
, n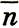 , λ
, λ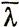 , р
, р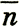 ,
, 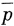 λ и т. д. Если спины направлены антипараллельно, то получаются частицы нулевого спина. Например, π+-мезон следует рассматривать как комбинацию р↑
λ и т. д. Если спины направлены антипараллельно, то получаются частицы нулевого спина. Например, π+-мезон следует рассматривать как комбинацию р↑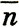 ↓. Действительно, заряд получается равным
↓. Действительно, заряд получается равным
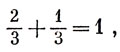
странность равна нулю, как то и нужно для π+-мезона. Хотите построить странный мезон, например К+? Значит, нужно взять комбинацию р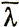 . Электрический заряд такой комбинации равен единице, плюс единице равна и странность. Чтобы получать бозоны целого спина, нужно подбирать пары кварков - антикварков с одинаково направленными спинами.
. Электрический заряд такой комбинации равен единице, плюс единице равна и странность. Чтобы получать бозоны целого спина, нужно подбирать пары кварков - антикварков с одинаково направленными спинами.
Пожалуй, не стоит выписывать всего этого подробно. Читатель, мы надеемся, поверит нам, что мезоны и бозонные резонансы, образуя свои супермультиплеты, так же аккуратно укладываются в рамки систематики, как и барионы.
Однако и этим не исчерпывается успех теории. Предположив, что кварки обладают магнитными моментами, пропорциональными их зарядам, можно найти соотношение между магнитными моментами составляемых из этих кварков частиц - например, найти отношение магнитных моментов протона и нейтрона. Оно получается равным3/2. А опыт дает значение 1,46. Опять-таки нельзя не признать, что совпадение блестящее.
...И яснее вырисовываются трудности
В тот самый момент, когда наш рассказ о кварках, казалось, достиг апогея, когда читатель, возможно, уже почувствовал к ним доверие и симпатию, вдруг появилось, да еще выделенное шрифтом, слово "трудности". Такой поразительный успех, даже, можно сказать, триумф, такое блестящее предсказание новой частицы - даже если не говорить об упорядочении частиц уже известных,- такое изящное объяснение свойств этих частиц, например соотношения между их магнитными моментами, - и вдруг "трудности"!
Какие? В чем?
Когда Гелл-Манна спросили, существуют ли кварки (напомним, что он в значительной мере и ввел их в науку), ответ гласил: "Кто знает?..."
Действительно, этого мы пока не знаем. (Не напоминает ли это вам ситуацию с векторным бозоном - переносчиком слабых взаимодействий, о котором мы знаем уже почти все, кроме того, существует ли он в природе?) Может быть, нечто рациональное, что бесспорно содержится в систематике частиц, мы напрасно поспешили истолковать в духе наглядных моделей "кирпичиков в кирпичиках"?
Сторонники кварков ищут подтверждения своих взглядов даже в исторических параллелях. Они ссылаются, например, на молекулярную теорию, которая была сформулирована до того, как появились прямые доказательства существования молекул. Тогда можно было бы говорить, что явления протекают так, "как если бы существовали молекулы". Но ведь теперь мы знаем, что молекулы действительно существуют.
Правда, на эту параллель можно ответить другими, не менее поучительными. Максвелл строил электродинамику, исходя из представлений о светоносном эфире, - но теперь мы знаем, что такого эфира нет. Фурье вывел используемые и сегодня уравнения теплопроводности, считая, что носителем тепла является некая всепроникающая жидкость, - но ведь сейчас мало кто вспоминает о теплороде, разве что историки естествознания.
Исторические параллели - штука деликатная.
Однако зачем, - спросите вы, - прибегать к каким-то туманным и неубедительным аргументам вместо того, чтобы просто обратиться к опыту? Нельзя ли попытаться экспериментально обнаружить кварки? Тем более, что кварки ввиду дробности их заряда должны быть в свободном состоянии устойчивыми и заметно выделяющимися на фоне других частиц.
Поиски кварков ведутся. Проще всего, казалось бы, не искать, а создавать их, осуществляя столкновения разогнанных на ускорителях частиц. Что может быть проще: ведь если все частицы состоят из кварков, то достаточно взять любую из этих частиц, стукнуть по ней чем-нибудь посильнее - и осколки-кварки так и брызнут во все стороны.
По идее, конечно, просто. Но никому никогда еще это не удавалось проделать. У нас нет пока достаточно мощных ускорителей.
Но такие ускорители есть у природы. Среди космических частиц, прилетающих к границам земной атмосферы, хотя и не очень часто, но появляются частицы с поистине космическими энергиями. Столкнувшись с ядрами атомов, входящих в состав атмосферы, такие частицы-силачи должны были бы породить свободные кварки. Как уже говорилось, по нынешним представлениям свободные кварки являются стабильными частицами и судьба их после рождения может быть примерно такой: кварки в окружении притягивающихся к ним "обычных" частиц (которые, кстати, не могут их полностью электрически нейтрализовать, так как несут целые заряды) образуют относительно большие "сгустки". Эти сгустки, опускаясь, достигнут поверхности Земли или, что для нас более интересно, попадут в океан. В океане такие сгустки должны постепенно опускаться на дно, следовательно, в придонных слоях концентрация их должна быть относительно большой. Остается совсем пустяк - зачерпнуть воду со дна, выпариванием, например, все увеличивать и увеличивать концентрацию и получать если не буквально кварковую кашицу, то нечто отдаленно ее напоминающее.
Таких опытов пока не было. Более того, пока нет и уверенности, не слишком ли мы легко и бесцеремонно диктуем кваркам нормы их поведения. Так ли мы уж много знаем об этих гипотетических частицах? Вот, например, такой вопрос: строя кварковые модели известных нам элементарных частиц, мы, в общем, действовали почти так же, как ребенок, строящий домик из кубиков. Но кубики поставишь - и они стоят неподвижно. С кварками сложнее. Те системы, которые мы пытаемся из них строить, должны быть динамическими, хотя бы из тех соображений, что общие принципы квантовой механики запрещают частицам, запертым в маленьком объеме, быть неподвижными. Кварки не могут стоять по стойке смирно - скорее можно говорить, что они водят хороводы. Однако эти хороводы мы почему-то совсем не учитывали в нашей классификации. Попытки такого учета делаются, достигнут некоторый успех, но общая ситуация с учетом движения кварков далека от полного благополучия.
Вопросы внутренней динамики кварков тесно связаны еще с одной принципиальной проблемой - проблемой сил, связывающих кварки в системы. То, что межкварковые взаимодействия существуют, понятно без пояснений. Больше того, мы знаем, что энергия этих взаимодействий очень велика. Ведь иначе достаточно было бы даже относительно слабого удара по любой частице - и она разбивалась бы на кварки. Громадными должны быть энергии взаимодействия кварков - а, значит, и дефекты масс. Если в атомных ядрах дефект массы составляет доли процента от общей массы, то в составленных из кварков частицах он недалек от ста процентов. Масса кварков, как принято сейчас считать, в 7 - 10 раз больше нуклонной. Протон состоит из трех кварков - их общая масса порядка двадцати - тридцати масс нуклона. Как же это может быть, что из частей весом в 30 единиц составляется целое, весящее одну единицу? Мы теперь понимаем - как. Значит, при образовании этого целого выделилась энергия, эквивалентная 29 единицам массы. И такой же является энергия связи.
Энергия грандиозная, ни с чем нам известным не сравнимая! Ко какие же силы могут так цементировать кварки? Какова природа межкварковых взаимодействий? И имеют ли эти взаимодействия какую-то единую природу?
Наконец, в каком соотношении они находятся с уже известными нам силами? Не сводятся ли, например, ядерные силы, которые мы истолковали как проявление обмена нуклонов мезонами, к каким-то частным видам проявлений взаимодействия между кварками - ведь и нуклоны состоят из кварков и мезоны также, согласно нашей модели, суть кварк-антикварковые пары.
Все эти и много других вопросов встают перед нами.
Часто об этом говорят коротко: нужно исследовать динамическую подоплеку новой систематики частиц.
Многого мы еще не знаем. Не можем мы, в частности, четко ответить и на вопрос, поставленный в начале книги: сколько существует фундаментальных типов взаимодействия (хотя еще недавно мы были почти уверены, что таких типов всего четыре).
Пятая сила?
Если кварков и нет в природе, то ведь группировка частиц в супермультиплет остается фактом и этот факт нужно как-то объяснить. Попытки такого объяснения имеются уже сейчас. Они появились даже раньше, чем возникла гипотеза кварков и связаны с допущением существования в природе не четырех, а пяти фундаментальных сил.
Выдвигается гипотеза о том, что сильное ядерное взаимодействие должно быть подразделено на два типа: очень сильное взаимодействие (О. С.) и умеренно сильное взаимодействие (У. С.) Очень сильное взаимодействие не зависит от странности и одинаково для всех частиц супермультиплета.
Умеренное сильное взаимодействие, напротив, зависит от странности (и изотопического спина) и поэтому различно для разных зарядовых мультиплетов, образующих данный супермультиплет.
Масса частиц, согласно современным представлениям, должна зависеть от тех взаимодействий, в которых они участвуют. Так вот, предполагается, что О. С. взаимодействие влияет на ту часть массы частиц супермультиплета, которая не зависит от странности и изотопического спина. Если бы никакого другого сильного взаимодействия, кроме О. С., не было, то частицы супермультиплета отличались бы по массе только за счет своих электрических зарядов. Тогда вместо супермультиплетов мы имели бы зарядовые мультиплеты, в которых различие масс (обычно небольшое) определяется электромагнитными силами. Гипотетическое У. С. взаимодействие зависит от странности и изотопического спина и как любое другое взаимодействие должно влиять на массу частиц. Поэтому оно приводит к зависимости масс частиц от странности и изотопспина и тем самым к образованию супермультиплетов. Зависимость масс от странности довольно велика, и по ней можно оценить интенсивность У. С. взаимодействия. Умеренно сильное взаимодействие должно быть слабее очень сильного взаимодействия примерно в 10 раз.
Таким образом, близнецами являются не только частицы внутри одного зарядового мультиплета, но и внутри одного супермультиплета. Близнецами к примеру являются π- и К-мезоны, и лишь странность, как некая маска, не позволяет это видеть непосредственно. Близнецы в "странных масках" и различных "электрических одеждах" - вот что такое с точки зрения представлений о двух типах сильного взаимодействия семейство частиц одинакового спина, входящих в данный супермультиплет. Та или иная комбинация "одежды" и "маски" определяет "внешний" облик частицы.
Умеренно сильное взаимодействие, если оно действительно существует, будет уже пятой силой в природе. Но, разумеется, никакой уверенности в ее существовании сейчас нет.
Мы твердо знаем, что наше понимание природы стало более глубоким. Новые идеи, в частности новая классификация элементарных частиц, - даже если оставить в стороне действительно замечательные открытия, которые здесь сделаны, - имеют непреходящее значение уже и потому, что они смело ставят вполне конкретные вопросы, намечают пути исканий. И даже если допустить, что завтра будет на опыте доказано, что кварков в природе не существует или что введение двух типов сильного ядерного взаимодействия не соответствует действительности, это не зачеркнет завоеванного, не зачеркнет успехов систематики, а лишь явится свидетельством того, что наши модели были лишь приближенными слепками с великого оригинала - Природы.
|
ПОИСК:
|