Как получить голограмму

Методы регистрации фазы электромагнитной волны хорошо известны и основаны на явлении интерференции. Рассмотрим простейший пример, показанный на рис. 1. Пусть на светочувствительную поверхность экрана под некоторым углом наклона падает плоская световая волна с неизвестными амплитудой А и фазой φ. Такая волна приведет к равномерному почернению поверхности экрана, причем степень почернения будет пропорциональна интенсивности волны, то есть А², времени ее воздействия.

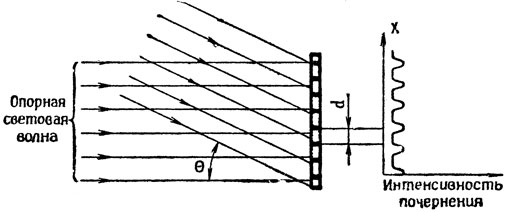
Рис. 1

Предположим теперь, что на экран падает еще одна плоская волна перпендикулярно экрану, которую мы будем называть опорной, эталонной или вспомогательной волной (лучом). Если частота и поляризация вспомогательной волны те же, что и у исходной, то падающие на экран волны будут когерентны и между ними возникнет интерференция, то есть в одних местах они будут усиливать, а в других - ослаблять друг друга. В результате этого на поверхности экрана появятся темные и светлые полосы.

Поскольку амплитуда и фаза вспомогательной волны известны, то по характеру интерференционной картины можно легко определить амплитуду и фазу исходной волны. Действительно, обозначим амплитуду вспомогательной волны через В, а фазу примем равной нулю. Тогда интенсивность

суммарного поля на поверхности светочувствительного экрана будет равна:

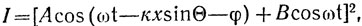
(1)

где θ - угол между направлениями распространения волн;

ω - частота волн;

κ=2π/λ;

λ - длина волны;

х-координата точки на светочувствительной поверхности.

Усредняя эту величину во времени (такое усреднение производит светочувствительный слой, а при наблюдении интерференционной картины на матовом стекле - человеческий глаз), получим:

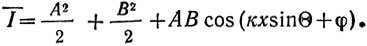
(2)

Эта величина, характеризующая интерференционную картину, пропорциональна степени почернения фотослоя (см. рис. 1), поэтому отсюда легко определить амплитуду исходной волны:

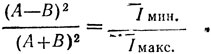
(3)

Фазу исходной волны также можно легко определить из соотношения (2). Если, например, принять, что в местах наибольшего почернения cos(кх sinθ+φ)=1, то

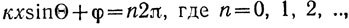
(4)

откуда

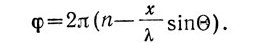
Таким образом, мы показали, что амплитуду и фазу исходной электромагнитной волны легко определить, рассматривая результат интерференции этой волны со вспомогательной плоской волной. Интерференционная картина, которую мы получили и которая описывается формулой (2), является дифракционной решеткой и представляет собой простейшую голограмму. Действительно, исходную волну, которая наклонно падает на светочувствительный слой, можно рассматривать как результат отражения ее от плоского зеркала: это означает, что мы получили голограмму объекта, представляющего собой плоское зеркало. Разумеется, это слишком простой пример получения голограмм, но в принципе излучение, рассеянное сложным объектом, можно рассматривать как сумму плоских волн, распространяющихся под разными углами. Естественно, в этом случае интерференционная картина получится весьма сложной, и мы уже не сможем описать голограмму простой формулой. Но тем не менее общность протекающих процессов очевидна, и следствия, вытекающие из рассмотренного примера, пригодятся нам в дальнейшем.

Что же нам необходимо отметить? Во-первых, вся информация, которую несут световые волны, отраженные от объекта, может быть записана в виде голограммы, то есть интерференционной картины, возникающей в результате взаимодействия этих волн с опорной, вспомогательной волной. Во-вторых, амплитуды и фазы (волн, несущих изображение объекта, фиксируются определенным законом распределения почернения на светочувствительной поверхности. В-третьих, получение голограмм обязательно требует когерентности опорной волны и волны, рассеиваемой объектом; в оптическом диапазоне такая когерентность обеспечивается применением лазеров.