Глава VIII. В погоне за точностью

Со времени первого определения скорости света прошло больше трехсот лет. Для истории науки это огромный отрезок времени. За эти триста лет многие физические проблемы перестали интересовать ученых и перекочевали со страниц научных журналов на страницы учебников. На смену им пришли новые вопросы. А какова же судьба скорости света? Ждет ли ее такая же участь? Современная физика решительно утверждает: нет, история скорости света не закончена! Свидетельством тому служат работы по измерению скорости света, выполненные в последние годы.

Резкое повышение точности измерения скорости электромагнитных волн произошло после Второй мировой войны. Исследования, проведенные в военных целях, кроме угрозы существованию человечества, принесли и множество важнейших чисто научных результатов. Один из них - развитие техники сверхвысоких частот (СВЧ). Были созданы генераторы и приемники излучения, работающие в диапазоне длин волн от одного метра до нескольких миллиметров. В СВЧ-диапазоне волн удалось провести очень точные и, что самое важное, независимые измерения частоты излучения υ и его длины волны λ. Это позволило определить скорость распространения СВЧ-излучения, просто умножив λ на υ:

Почему такой метод определения с удобен? Дело в том, что длины волн порядка 1 см можно определить с очень высокой точностью, применяя интерферометрические методы. При больших длинах волн это сделать очень трудно. Представьте, какие размеры должен иметь интерферометр, работающий на длине волны в сотни метров! В условиях, когда длина волны сравнима с характерными размерами используемых в опытах приборов, начинают сказываться дифракционные эффекты, которые довольно трудно учесть. При использовании излучения коротковолновой части СВЧ-диапазона внести в результаты измерений поправки, связанные с дифракцией волн, относительно просто. Значительных проблем с определением частоты в СВЧ-диапазоне не возникает.

Конечно, не следует думать, что измерить величину с, используя новую технику, было очень просто. Каждый ученый, работавший в этой области, ставил перед собой задачу-максимум: провести предельно точные измерения λ и υ для получения возможно более точного значения с, а работа на пределе точности всегда сложна.

Определенным итогом измерения с в СВЧ-диапазоне стала работа американского ученого К. Фрума, результаты которой были опубликованы в 1958 г. Для определения длины волны Фрум использовал четырехрупорный интерферометр. СВЧ-генератор работал на частоте 72,006 ГГц (1 ГГц - один гигагерц - равен 10⁹ Гц), длина волны составляла λ ≈ 4,2 мм. Успех Фрума во многом определился оригинальными методами, примененными для учета дифракционных эффектов. Ученый получил результат

В течение длительного периода эта величина с считалась наиболее точной.

Для того чтобы еще более повысить точность определения с, требовалось создание принципиально новых методов, которые позволили бы проводить измерения в области больших частот и, соответственно, меньших длин волн. Возможность разработки таких методов появилась после создания оптических квантовых генераторов - лазеров^*.

^* (Принцип действия лазеров описан во многих популярных книгах (см., например: Тарасов В. Л. Оптика, рожденная лазером. - М.: Просвещение, 1977), к которым мы и отсылаем читателей, интересующихся вопросами, связанными с созданием и применением оптических квантовых генераторов.)

Излучение лазеров обладает целым рядом особенностей. Во-первых, оно значительно более монохроматично, чем излучение других источников света. Это означает, что область частот, в которой сосредоточена большая часть энергии лазерного излучения, мала по сравнению со спектральными интервалами, характерными для других источников. Во-вторых, лазеры генерируют излучение высокой направленности. Наконец, излучение многих лазеров характеризуется исключительно высокой мощностью. Для проблемы определения с наибольшее значение имеет первое свойство лазерного излучения - монохроматичность, поскольку область частот Δυ, в которой происходит генерация, определяет предел точности измерения частоты. Первые лазеры характеризовались такими величинами Δυ, которые не позволяли надеяться на увеличение точности определения с. Проблема, в частности, состояла в том, что один и тот же лазер при различных внешних условиях, например, при разных температурах и способах настройки мог генерировать излучение различных частот. Хотя различие в частотах составляло всего одну миллионную часть (10^-6) самой частоты, попытка улучшить результат Фрума была явно обречена на неудачу, ведь точность измерений Фрума была ≈ 4 ⋅ 10^-7!

Таким образом, прежде чем браться за определение частоты лазера, необходимо было добиться ее высокой стабильности. Для решения этой задачи были применены новейшие достижения в области электроники, спектроскопии, технологии. В итоге стабильность частоты лазера была доведена до фантастической величины - 10^-11!^*. С излучением, обладающим такой стабильностью, уже можно было обратиться к проблеме определения скорости света.

^* (В настоящее время благодаря усилиям советских физиков стабильность частоты лазеров доведена до 10^-15. Данные о стабильности, приведенные в тексте, относятся к аппаратуре, примененной для определения с. )

Процесс измерения всегда прямо или косвенно сводится к сравнению неизвестной величины с эталоном. В наши дни в качестве эталона длины используется метр, определяемый как длина, на которой укладывается фиксированное число волн излучения изотопа криптона ⁸⁶Кr^**. Для конструирования эталона времени используются световые колебания, создаваемые атомами изотопа цезия ¹³³Cs. Таким образом, определение с сводится к сравнению длин волн излучения лазера и атомов ⁸⁶Кr и частот излучения того же лазера и атомов ¹³³Cs. Наибольшую сложность представляет измерение частоты лазерного излучения.

^** (1 метр - длина, равная 1650763,73 длины волны излучения в вакууме, соответствующего переходу между уровнями 2р₁₀ и 5d₅ атома ⁸⁶Kr. Такое излучение получают с помощью специальных ламп; в них криптон находится при низком давлении; стенки лампы охлаждаются жидким азотом, температура которого, благодаря непрерывной откачке паров, поддерживается равной 63 К. Интерференционные методы измерения позволяют определить длину эталона метра с точностью (2 ÷ 3) ⋅ 10^-9. )

Прямое сравнение эталонной частоты и частоты лазера практически невозможно. Поэтому физики предложили два косвенных метода определения частоты. Первый состоит в использовании модулированного лазерного излучения. Суть этого метода заключается в преобразовании излучения лазера с частотой υ в излучение, характеризуемое частотами υ₁ = υ + ƒ и υ₂ = υ - ƒ. Частота ƒ хорошо известна и задается СВЧ-генератором. Две волны с частотами υ₁ и υ₂ пропускаются через специальное устройство - интерферометр Фабри - Перо. Излучение разных частот проходит через интерферометр без значительного ослабления только в том случае, если выполняется определенное соотношение между υ₁, υ₂, длиной интерферометра и скоростью света. Если определить длину интерферометра для двух положений зеркал, при которых излучение обеих частот проходит через него с минимальным ослаблением, то, применив довольно простую математическую процедуру, можно найти частоту υ. С помощью этого метода группе американских физиков из Национального бюро стандартов удалось определить частоту излучения гелий-неонового лазера: υ = 473612166 ± 29 МГц. Легко рассчитать, что точность определения частоты в этих опытах составляла Δυ/υ ≈ 6 ≈ 10^-8.

Второй способ ближе по идее к непосредственному сравнению частоты лазера с эталоном. Он заключается в том, что с помощью специальных преобразователей излучение с хорошо известной частотой умножается, т. е. превращается в излучение с частотой, в целое число раз превышающей первоначальную. Этот же преобразователь может и "смешивать частоты", т. е. преобразовывать излучение с частотами υ₁ и υ₂ в излучение с частотой υ₃ = υ₁ + υ₂. В реальном эксперименте используют обе возможности. Сначала "умножают" достаточно большую фиксированную частоту одного источника, например, лазера, работающего в инфракрасном диапазоне, а затем ее "смешивают" с регулируемой частотой, которая характеризует излучение генератора СВЧ-диапазона - клистрона. Полученное таким образом излучение с высокой частотой направляется на специальный приемник, на который падает и излучение исследуемого лазера. В результате наложения, двух волн с несколько различающимися частотами сигнал, регистрируемый приемником, представляет собой биения. На рис. 36 показана зависимость сигнала U от времени t при возникновении биений. Чем меньше различаются частоты двух накладывающихся колебаний, тем больше различаются периоды колебаний огибающей сигнала и ее высокочастотного "наполнения". Регулировкой частоты клистрона можно добиться того, чтобы биения исчезли. Исчезновение биений происходит, когда частоты двух колебаний в точности совпадают. Поскольку частота излучения вспомогательного лазера и клистрона известна с высокой точностью, метод "нулевых биений" позволяет найти частоту излучения исследуемого лазера.

Принципиальная экспериментальная проблема, стоящая на пути реализации этого метода, состоит в том, что эффективность элементов, преобразующих излучение данной частоты в излучение с большей частотой, по мере приближения частот к области видимого света резко падает. Поэтому реально удается провести измерения описанного типа только в ближней инфракрасной области спектра. Так, в том же Национальном бюро стандартов США другая группа экспериментаторов измерила частоту инфракрасного излучения гелий-неонового лазера (λ = 3,39 мкм): υ = 88376,181627 ± 0,000050 ГГц.

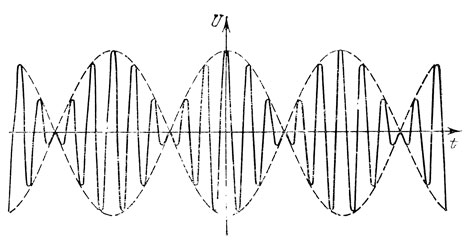
Рис. 36. Биения

Предложенный способ измерения частоты очень сложен с технической точки зрения. Не таится ли здесь опасность возникновения каких-либо неучтенных ошибок при определении υ? Ответ на этот вопрос дал сам эксперимент. Частота лазера другого типа, работающего на углекислом газе, была определена аналогичным методом в Национальной физической лаборатории в Англии. Она оказалась равной υ′ = 32176,079482 ± 0,000028 ГГц (λ′ = 9,3 мкм). Конечно, непосредственно сравнить величины частот, полученные американскими и английскими физиками, невозможно. Однако о правильности методики можно судить по результату расчета скорости света^*.

^* (Методы точного измерения длины волны излучения были разработаны значительно раньше, чем метод измерения частоты, поэтому определение λ считается обычной операцией, которую все исследователи проводят примерно с одинаковой точностью. )

Национальное бюро стандартов США

Национальная физическая лаборатория Англии

Точность определения с возросла по отношению к опытам Фрума практически в 100 раз! В то же время оба результата совпадают между собой в пределах точности проведенных измерений. Отметим, что способ определения частот с помощью модуляции лазерного излучения дает величину

Этот результат в пределах ошибки измерений согласуется с данными, приведенными выше, хотя и характеризуется большей относительной погрешностью.

Таким образом, достигнутая в настоящее время точность определения с составляет ≈ 3⋅10^-9. Возникла интересная ситуация: теперь точность определения с ограничивается уже не методами измерения частоты и длины волны, а неопределенностью стандарта длины - длины волны излучения атомов ⁸⁶Кr.

Такое положение заставляет по-новому подойти к выбору основных единиц измерения - единиц длины и времени. Если стандарт длины не удается определить с достаточной точностью, то, может быть, от него лучше отказаться совсем? В качестве стандартов можно выбрать, например, определенную частоту и ... скорость света, а длину определять с помощью вычислений. Если такое предложение будет принято, то на этом "кончится" история скорости света. Но произойдет ли это когда-нибудь?

Пока же конца проблемам, связанным с "самой большой скоростью", не видно. Многие из вопросов, о которых шла речь в этой книге, еще не получили окончательного ответа. Об этом красноречиво свидетельствуют заголовки статей, встречающихся на страницах научных журналов в наши дни. Как ответ на вопрос, стоящий в названии одной из глав нашей книги, "Сколько у света скоростей?", звучит заголовок "Восьмая скорость света". А какие мысли будит у физика статья, озаглавленная "Действительно ли скорость света не зависит от скорости движения источников?".

Физики продолжают исследовать вопрос о постоянстве скорости света во времени. Пока указаний на изменение с с течением времени нет, но физика не может безоговорочно отбросить такую возможность. Что ж, остается ждать сообщений о новых измерениях скорости света. Эти измерения могут дать еще много нового для познания природы, неисчерпаемой в своем разнообразии.