Единицы Планка

В микромире нет своего масштаба длины. Из двух постоянных ћ u c нельзя составить величину с размерностью длины или времени. Для этого надо взять еще массу. Тогда длину можно, например, составить так: ћ/тс.

В общей теории относительности также нет масштаба длины, так как его нельзя составить из γ и с. Но если привлечь на помощь массу, то длину можно составить так: γт/с².

Объединим теперь обе длины ћ/тс и γт/с², составив их геометрическое среднее (ћ γ/c³)^1/2. При этом масса сократится. Это и есть единица длины, предложенная Планком.

После того как Планк ввел две фундаментальные постоянные ћ и k, он заметил, что появилась возможность построить новую систему единиц, не связанную ни с какими искусственными эталонами. Это следующие единицы:

Единицы Планка удобны при расчете таких систем, где существенны эффекты как квантовые, так и гравитационные.

Но единицы Планка не только удобны, они обладают принципиальной особенностью. Их существование означает, что в природе, во Вселенной есть единственные масштабы, связанные одновременно и с квантовыми, и с релятивистскими свойствами мира. Постоянная Планка определила связь между энергией и частотой (масштаб кванта), скорость света - связь между массой и энергией (масштаб энергии). Естественно было предположить, что и единицы Планка определяют масштабы характеристик каких-то событий или объектов. Черная дыра (и ее энтропия) кажется удачным кандидатом для применения единиц Планка.

Предположим, что масштаб энтропии связан с постоянной длины l_n, т. е. что площадь поверхности черной дыры надо разделить на l²n с каким-то коэффициентом, о котором, конечно, нельзя догадаться заранее. На основе таких, надо сознаться, не очень строгих рассуждений и была выдвинута гипотеза о том, что энтропия черной дыры должна иметь вид 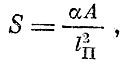, где коэффициент α надо вычислить из каких-то соображений особо. Такая догадка оказалась правильной. Коэффициент α был вычислен позднее Хоукингом. Он оказался равным 1/4.

Зная энтропию, можно вычислить и температуру. Заменим площадь А ее выражением через гравитационный радиус:

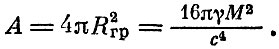
Используя единицы Планка, можно теперь написать формулу для энтропии:

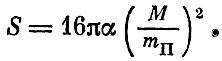
Температура запишется в виде

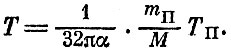
Исключая из этих формул массу, будем иметь (в единицах Планка и α=1/4)

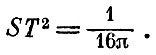
Такое уравнение состояния ни на что не похоже. Из него следует, что чем выше температура, тем меньше энтропия, а при абсолютном нуле энтропия обращается в бесконечность.

Отсюда можно заключить, что либо в наших рассуждениях грубая ошибка, либо с черной дырой происходит нечто серьезное и она не "доживает" до абсолютного нуля. Но в рамках классических представлений парадокс разрешить оказалось невозможным.