Высокотемпературная сверхпроводимость

Рассказ о том, как получают низкие температуры, был ограничен идеями о методах их получения. Мы сознательно не описывали физические явления, происходящие при низких температурах, считая, что физика низких температур - большая самостоятельная область, требующая отдельной книжки. Кстати, такая книжка в "Библиотечке "Кванта" есть и мы советуем ее прочесть^*. Но совсем недавно, весной 1987 г., произошли столь важные события, которые так сильно взволновали физиков, что было бы обидно о них не рассказать, хотя бы в краткой форме.

^* (Эдельман В. С. Вблизи абсолютного нуля,- М.: Наука, 1983.- (Библиотечка "Квант", вып. 26).)

В январе 1987 г. были открыты новые сверхпроводящие материалы, которые полностью теряют свое сопротивление при температуре около 40 К, а месяцем-двумя позже был открыт сверхпроводник с T_c=93 К (T_c - критическая температура, при которой наступает сверхпроводимость) .

Поводов для сенсации было, по меньшей мере, два. До этого открытия рекорд по температуре T_c держал сверхпроводник, представляющий собой соединение ниобия и германия Nb₃Ge с температурой перехода 23,2 К. Все попытки найти соединение с большей T_c многие годы не приводили к успеху. Второй повод более серьезный. Температура 93 К выше температуры жидкого азота 77 К. Это значит, что достаточно погрузить такой образец в азот, и он станет сверхпроводником. Жидкий азот получать значительно проще, чем жидкий гелий, с помощью которого охлаждали сверхпроводники до сих пор, и поэтому он существенно дешевле. Открывается путь к очень широкому практическому использованию сверхпроводников. Конечно, предстоит преодолеть еще много технических трудностей, но задача настолько многообещающая, что они будут решены. Было бы хорошо найти сверхпроводник, который сохранял бы свои свойства даже при комнатной температуре, тогда проблема стала бы совсем простой, и, кажется, природа идет нам навстречу.

Надо надеяться, что когда Вы, читатель, будете читать эти строки, то Вы уже будете знать больше, чем здесь написано. Запомните два имени - это Майер и Беднорц из Физической лаборатории в Цюрихе, они первыми сообщили о новых сверхпроводниках. Сейчас сотни лабораторий мира, в том числе и лаборатории в Москве, Ленинграде, Свердловске, Дубне и других городах Советского Союза, вступили в увлекательное соревнование, исследуя новое явление - высоко температурную сверхпроводимость. Полезно сейчас разобрать только главный вопрос - попытаться ответить, почему электроны в металле перестают терять энергию, сталкиваясь с атомами и ионами, образующими кристаллическую решетку - жесткий остов металла. Электрический ток - поток электронов - можно уподобить потоку жидкости. В нормальных условиях электронная жидкость испытывает "трение" - электроны все время передают часть своей энергии колебаниям ионов в решетке; равновесное течение тока устанавливается тогда, когда такие потери (можно говорить о "вязкости" потока электронов) уносят всю энергию, поступающую от источника тока. В результате работа источника тока идет на нагревание решетки; так же как рабочее тело в цикле Карно, электроны играют роль передатчика энергии. Стоит только отключить источник тока, повернув выключатель, как вся энергия электронов растратится на столкновение с решеткой, иначе говоря, на ее разогрев, и ток очень быстро затухнет. Колебания решетки в квантовой механике описываются очень похоже на то, как описывается электромагнитное поле. Электромагнитное поле можно, как мы знаем, описывать как совокупность квантов - фотонов, образующих нечто вроде газа. Колебания решетки также можно описывать, как газ фононов (название было придумано Я. И. "Френкелем), который описывается формулой, почти совпадающей с формулой Планка. Электронам в металле отведена роль поглощать и излучать фононы, вступая с ними в тепловое равновесие.

Чем ниже температура, тем меньше вероятность излучения фонона, тем меньше энергии теряет электрон. Сопротивление потоку электронов уменьшается. Теория показывает, что в металле электрическое сопротивление оказывается пропорциональным термодинамической температуре (при низких значениях температуры):

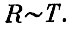
Заметим, что обычно говорят не о сопротивлении R (в омах), а об удельном сопротивлении р (в Ом*м) или о проводимости о (в Ом^-1*м^-1). Последняя связывает плотность тока j с напряженностью электрического поля Е:

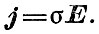
Сопротивление R зависит от длины и площади поперечного сечения проводника, р и σ зависят только от свойств материала. Поэтому в таблицах помещают значения р.

Формула для сопротивления р ∼Т наводит на мысль, что при Т → 0 сопротивление будет также стремиться к нулю и что, взяв кусок металла, мы можем сделать из него идеальный термометр, который может показывать температуру вплоть до абсолютного нуля. Однако это не так. Формула р ∼Тверна только для идеального кристалла. Если в кристалле есть какие-нибудь примеси или если в нем как-то нарушена стройность кристаллической решетки - выбиты атомы, сдвинуты как-то целые слои, то при приближении к Т=0 сопротивление перестает уменьшаться. Остается остаточное сопротивление, которое и дискредитирует идею простого термометра.

Исчезновение сопротивления у сверхпроводника имеет совсем другой характер. По мере охлаждения и приближения к критической температуре^* сопротивление падает, а в точке Т_c скачком исчезает практически до нуля. По данным измерений для сверхпроводников удельное сопротивление р<10^-10 Ом*м.

^* (Заметим, что Т_c - хорошие постоянные, которые используют в качестве опорных точек для градуирования термометров.)

В лабораторных условиях, в которых получались новые высокотемпературные сверхпроводники, падение сопротивления происходит в интервале порядка 1 К, да и этот интервал скорее всего связан с какими-то дефектами в образцах.

Итак, поведение сверхпроводника носит совсем по тот характер, который надо было ожидать на основании простых физических соображений. Чтобы электронная жидкость текла без трения через кристаллическую решетку, надо, чтобы существовал какой-то запрет на передачу энергии от электронов к решетке. Такой запрет, более сильный, чем тот, который приводит к закону р ∼Т, придумать нельзя. Поэтому сверхпроводимость долгое время не находила своего объяснения. В связи с этим можно вспомнить исторический анекдот, который рассказывают об Ампере. Ампер, как известно, придумал объяснение магнетизму, увидев источник магнетизма в токах, текущих по маленьким круговым орбитам. Ампер, конечно, ничего не знал ни об элементарных зарядах, ни о самих электронах, и объяснение его было только словесным. Но оппоненты ему немедленно возразили, что текущий ток должен нагревать образец - магнит же, как все знают, остается холодным! Надо сказать, что возражение это было убийственным и опровергнуть его в то время, строго говоря, было невозможно; о квантовых орбитах узнали только в нашем веке.

Электроны в атомах подчиняются законам квантовой механики и двигаются, ни с кем не сталкиваясь.

Однако и это квантовое явление не помогает нам понять, как электроны двигаются не по замкнутым орбитам, а прямолинейно, образуя ток сверхпроводимости. Когда в 1912 г. Каммерлинг-Онес впервые открыл сверхпроводимость ртути (Т_c=4 К), он вовлек физиков в проблему, решение которой выходило за пределы всего того, что они знали из прошлого опыта. Думать стало немного легче лишь много позже после того, как была открыта (П. Л. Капицей в 1939 г.) сверхтекучесть гелия и когда в 1941 г. Л. Д. Ландау создал теорию этого явления. Опять отсылая читателя к книге В. С. Эдельмана за подробным обсуждением свойств изотопов гелия ³Не и ⁴Не, напомним только, что жидкий ⁴Не сверхтекучий, он может вытекать без трения через тонкую щель. (Такой гелий, лишенный вязкости, называют Не II.)

Электроны - не атомы гелия. Электроны заряжены, у них есть спин и к ним теория Ландау неприменима. Тем не менее природа проявила свою щедрость: оба явления - сверхтекучесть гелия II и сверхпроводимость - оказались все же связанными друг с другом,

Объяснить все очень трудно. Попробуем хотя бы понять, что происходит с гелием. Мы говорим, что жидкость состоит из атомов и атомы движутся как материальные точки. Но у жидкого гелия есть и другие степени свободы: это волны, которые охватывают большие объемы, и их распространение связано с тем, что многие атомы движутся в такт, музыкант сказал бы, в унисон. Физики говорят о когерентном движении. Такие колебания жидкости - говорят о ее макроскопических степенях свободы - образуют систему, похожую на газ, в том же смысле, в каком электромагнитные колебания образуют газ фотонов. В квантовой механике кванты колебаний ведут себя подобно частицам. Колебания в гелии, однако, отличаются от фотонов тем, что фотоны могут распространяться как в веществе, так и в пустоте, а волны в гелии (как и фотоны в кристалле) в пустоте "не живут". Их нельзя считать частицами в полном смысле этого слова, и их принято называть квазичастицами: о них говорят как о возбуждениях среды.

Газ таких возбуждений описывается почти такой же формулой Планка, как и фотоны. Как оказалось, в этом и есть разгадка. Бозе-газ, так называют систему квазичастиц, описываемую формулой Планка, обладает способностью конденсироваться, собираться на самом низком уровне энергии, образуя бозе-конденсат. Вырвать частицу из бозе-конденсата очень трудно - она будет стремиться вернуться обратно, так как вероятность возвращения пропорциональна числу частиц в конденсате. Именно это свойство делает конденсат устойчивой системой, именно оно препятствует передаче энергии от гелия к стенкам. Гелий II состоит (так можно характеризовать ситуации) из двух жидкостей, обычной и сверхтекучей. Основываясь на такой модели, Ландау и построил теорию сверхтекучести. Не следует, конечно, представлять себе, что две жидкости разделены в пространстве, они присутствуют во всех объемах жидкости, и их нельзя разделить друг от друга. Все это подробно описано в упомянутой выше книге Эдельмана.

Сверхпроводимость, как это выяснилось после появления теории Бардина, Купера и Шлифера (теория БКШ), оказалась очень похожей на теорию сверхтекучести. Мостик между двумя теориями возник после того, как было доказано, что электроны в сверхпроводнике объединяются в пары (куперовские пары) с полным импульсом и полным спином, равным нулю. Механизм объединения связан с колебаниями кристаллической решетки - фононами. Электроны обмениваются фононами точно так же, как они обмениваются фотонами. Это значит, что один электрон раскачивает решетку, а другой решеткой раскачивается. В результате возникает притяжение электронов (это доказывается вычислениями). Если притяжение электронов превышает их электрическое отталкивание, то образуется связанная пара, которая ведет себя почти как атом гелия. Так возникает сверхтекучий конденсат. Чтобы не возникло неправильного представления, надо отметить, что куперовские пары имеют большие размеры, превышающие расстояние между атомами решетки, так что речь идет скорее не о связанных парах, а о согласованном движении двух частиц, находящихся друг от друга на большом (в атомных масштабах) расстоянии. Такие пары образуют квантовую жидкость, которая не может передавать энергию решетке. В этом смысле сверхтекучая жидкость находится в самом низком устойчивом состоянии и одновременно способна обладать общей скоростью и протекать без потерь через кристаллическую решетку. Чтобы вернуть сопротивление, надо повысить температуру и разрушить куперовскую пару. Энергия связи такой пары и определяет величину критической температуры. Конденсат куперовских пар можно представлять себе как почти изолированную систему, находящуюся при температуре абсолютного нуля. К сожалению, эту систему нельзя отделить от всего остального, нельзя выкачать газ куперовских пар из куска металла - он существует только как система возбуждения электронной "жидкости". Такую изощренную форму приобретает термодинамика.

Можно еще добавить, что сверхпроводник с T_c=93 К представляет собой соединение YВа₂Сu₃О_6,81 В этом соединение медь входит двумя различными способами: как двухвалентная и трехвалентная. Такое соединение (иттрий - барий - медь - кислород) имеет необычное строение. Атомы меди и кислорода образуют регулярные двумерные слои, между которыми располагаются два слоя одномерных цепочек СuО. Именно эти слои и цепочки определяют сверхпроводимость. Наверное, много интересного откроется перед нами в ближайшее время. Но уже сейчас нельзя не изумляться все новыми и новыми открытиями красоты нашего удивительного мира.