Из пушки на Луну

В 1865-1870 гг. появился фантастический роман Жюль-Верна "Из пушки на Луну", в котором высказана необычайная мысль: послать на Луну исполинский пушечный снаряд-вагон с живыми людьми! Жюль-Верн представил свой проект в столь правдоподобном виде, что у большинства читателей, наверное, возникал вопрос: нельзя ли в самом деле осуществить эту мысль?

За истекшие три четверти века техника так далеко ушла вперёд в деле сооружения огромных пушек, так увеличила силу взрывчатых веществ, что, быть может, фантазия французского романиста сейчас близка к реальному воплощению?

Об этом интересно побеседовать.

Итак, возможно ли послать снаряд на Луну?

Сначала рассмотрим, можно ли - хотя бы только в теории - выстрелить из пушки так, чтобы снаряд никогда не упал назад на Землю. Теория не возражает против такой возможности. В самом деле, почему снаряд, горизонтально выброшенный пушкой, в конце концов падает на Землю? Потому что Земля, притягивая снаряд, искривляет его путь; он летит не по прямой линии, а по кривой, направленной к Земле, и поэтому рано или поздно встречается с почвой. Земная поверхность, правда, тоже искривлена, но путь снаряда изгибается гораздо круче. Если же кривизну пути снаряда ослабить и сделать её одинаковой с искривлением поверхности земного шара, то такой снаряд никогда не сможет упасть на Землю! Он будет двигаться по кривой, концентрической с окружностью земного шара; другими словами - сделается его спутником, как бы второй Луной.

Рис. 29. Вычисление скорости снаряда, который должен навсегда покинуть Землю

Но как добиться, чтобы снаряд, выброшенный пушкой, шёл по пути, менее искривлённому, чем земная поверхность? Для этого необходимо только сообщить ему достаточную скорость. Обратите внимание на рис. 29, изображающий разрез части земного шара. На горе в точке А стоит пушка. Снаряд, горизонтально выброшенный ею, был бы через секунду в точке В,- если бы не существовало притяжения Земли. Но притяжение меняет дело, и под действием этой силы снаряд через секунду окажется не в точке В, а на 5 м ниже, в точке С. Пять метров - это путь, проходимый (в пустоте) каждым свободно падающим телом в первую секунду под действием силы тяжести близ поверхности Земли. Если, опустившись на эти 5 м, снаряд наш окажется над уровнем Земли ровно настолько же, насколько был он в точке А, то, значит, он мчится по кривой, концентрической с окружностью земного шара.

Остаётся вычислить отрезок АВ (рис. 29), т. е. тот путь, который проходит снаряд в секунду по горизонтальному направлению; мы узнаем тогда, с какою секундною скоростью нужно для нашей цели выбросить снаряд из жерла пушки. Вычислить это нетрудно из треугольника АОВ, в котором ОА - радиус земного шара (около 6 370 000 м);ОС = ОА, ВС = 5 м; следовательно, ОВ = 6 370 005 м. Отсюда, по теореме Пифагора, имеем

Сделав вычисление, находим, что искомая скорость АВ = около 8 км в сек.

Итак, если бы не было воздуха, который сильно мешает быстрому движению, снаряд, выброшенный из пушки со скоростью 8 км, никогда не упал бы на Землю, а вечно кружился бы вокруг неё, подобно спутнику. Такой скорости наши пушки дать не могут: современные орудия сообщают снарядам скорость вчетверо меньшую.

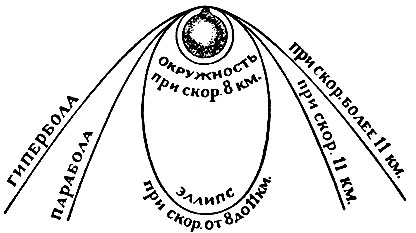
Рис. 30. Судьба пушечного снаряда, выпущенного с начальною скоростью 8 и более километров

А если выбросить снаряд из пушки с ещё большею скоростью,- куда полетит он? В небесной механике доказывается, что при скорости в 8, 9, даже 10 км снаряд, вылетев из жерла пушки, должен описывать вокруг земного шара эллипс тем более вытянутый, чем больше начальная скорость. При скорости же снаряда около И км он вместо эллипса опишет уже незамкнутую кривую - "параболу", навсегда удаляясь от Земли (рис. 30).

Мы видим, следовательно, что теоретически мыслимо было бы полететь на Луну внутри снаряда, выброшенного с достаточно большой скоростью^*.

^* (Тут могут представиться, однако, затруднения совсем особого рода. Подробнее вопрос этот рассматривается во второй книге "Занимательной физики", а также в другой моей книге - "Межпланетные путешествия".)

(Предыдущее рассуждение имело в виду атмосферу, не препятствующую движению снарядов. В реальных условиях наличие сопротивляющейся атмосферы чрезвычайно затруднило бы получение таких высоких скоростей, а быть может сделало бы их совершенно недостижимыми.)