Что тяжелее?

На одну чашку весов поставлено ведро, до краёв наполненное водой. На другую - точно такое же ведро, тоже полное до краёв, но в нём плавает кусок дерева (рис. 60). Какое ведро перетянет?

Я пробовал задавать эту задачу разным лицам и получал разноречивые ответы. Одни отвечали, что должно перетянуть то ведро, в котором плавает дерево,- потому что "кроме воды в ведре есть ещё и дерево". Другие - что, наоборот, перетянет первое ведро, "так как вода тяжелее дерева".

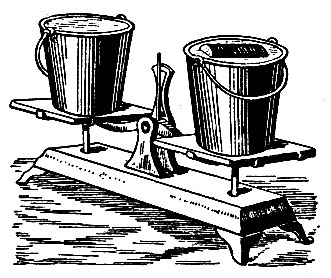
Рис. 60. Оба ведра одинаковы и наполнены водою до краёв; в одном плавает кусок дерева. Которое перетянет?

Но ни то, ни другое не верно: оба ведра имеют одинаковый вес. Во втором ведре, правда, воды меньше, нежели в первом, потому что плавающий кусок дерева вытесняет некоторый её объём. Но, по закону плавания, всякое плавающее тело вытесняет своей погружённой частью ровно столько жидкости (по весу), сколько весит всё это тело. Вот почему весы и должны оставаться в равновесии.

Решите теперь другую задачу. Я ставлю на весы стакан с водой и рядом кладу гирьку. Когда весы уравновешены гирями на чашке, я роняю гирьку в стакан с водой. Что сделается с весами?

По закону Архимеда, гирька в воде становится легче, чем была вне воды. Можно, казалось бы, ожидать, что чашка весов со стаканом поднимется. Между тем в действительности весы останутся в равновесии. Как это объяснить?

Гирька в стакане вытеснила часть воды, которая оказалась выше первоначального уровня; вследствие этого увеличивается давление на дно сосуда, так что дно испытывает добавочную силу, равную потере веса гирькой.