Механика древних и Архимед

Этот обзор мы начинаем с механики. На первом месте среди создателей механики стоит Архимед, имя которого вошло в историю физики навеки. Архимед родился в 287 г. до н. э. в Сицилии, в городе Сиракузах. Он был сыном астронома Фидия и родственником Герона, ставшего потом тираном Сиракуз. Вероятно, отец дал ему достаточное математическое образование: Архимед хорошо знал вышедшие незадолго до его рождения "Начала" Эвклида. Дальнейшее образование и научное развитие Архимед получил в Александрии. Здесь он занимается астрономией, математикой и механикой. Но уже в александрийский период отчётливо выявились научные интересы Архимеда, а именно - проблемы механики. Даже в своих астрономических занятиях Архимед прославился изобретением механических аппаратов. Таков был прибор для измерения видимого диаметра Солнца и знаменитая "сфера", т. е. планетарий, повидимому, приводившийся в движение водяным двигателем. Здесь же был изобретён им водоподъёмник и здесь же он, вероятно, пришёл к своим знаменитым исследованиям о центрах тяжести и рычагах, в тесной связи с которыми находились и его математические работы.

Архимед

По возвращении из Александрии вся остальная деятельность Архимеда протекала в родном городе, вплоть до самой гибели, совпавшей с падением Сиракуз. Самоотверженная работа Архимеда при защите города была предметом особого удивления древних. Приведём рассказ римского историка Плутарха из биографии полководца Марцелла, относящийся к осаде Сиракуз этим полководцем.

"Марцелл приближался и по суше, и морем. На суше войско шло под командою Аппия, а сам Марцелл плыл во главе шестидесяти галер о пяти рядах вёсел, снабжённых всякого рода метательными снарядами и оружием. Восемь судов, соединённых вместе, составляли род обширного помоста, на котором возвышалась стенобитная машина. Так плыл он к городу, доверяясь громадности и могуществу приготовлений и своей репутации. Всё это не смутило, однако, Архимеда. Что всё это значило в сравнении с его машинами?"

В этом месте Плутарх делает отступление, ярко характеризующее умонастроения древних и иллюстрирующее сделанные выше замечания о характере науки рабовладельческого общества:

"Не должно думать, впрочем, чтобы сам он придавал им большую цену. Для него это были большею частью как бы игрушки геометрии. Он исполнил их, уступая почётным настояниям царя Гиерона. Гиерон убеждал Архимеда перенести на время душевную мощь свою от умственных вещей к телесным и дать толпе возможность ощутить силу его соображений, соединив их с практическими, полезными применениями. Механика, предмет искания и прославления, есть изобретение Эвдокса и Архита. Они хотели некоторым образом иллюстрировать геометрию (дать геометрии внешнюю прикрасу) и основать на чувственных и материальных примерах теоремы, которые трудно решить помощью рассуждений и научных доказательств. Так, для теоремы о двух средних пропорциональных, для разрешения которой мало одних рассуждений и которая, однако, необходима по отношению ко многим фигурам, они прибегли к механическим средствам и составили род мезолябии при помощи кривых линий и конических сечений. Но скоро Платон в негодовании стал упрекать их, что они портят геометрию, лишают её достоинства, обращают в беглого раба, заставляя её от изучения бестелесных и умственных вещей переходить к чувственным предметам и прибегать, кроме рассуждения, к помощи тел,рабски изготовленных работою руки. Так униженная механика была отделена от геометрии. Она стала одним из военных искусств".

Вот как смотрели древние на практику и опыт! Касаясь специально Архимеда, Плутарх говорит:

"Построение машин и всё искусство, направленное на удовлетворение житейских потребностей, были в его глазах чем-то неблагородным, низкоремесленным. Он полагал своё честолюбие в изучении предметов, к красоте и совершенству которых не примешивается ничто, имеющее отношение к житейским потребностям; в науках, где доказательство и предметы соперничают в достоинствах: предмет доставляет величие и красоту, доказательства - точность и мощь, производящие чудеса".

Вернёмся теперь к красочному описанию осады Сиракуз римлянами.

"При двойной атаке римлян сиракузцы онемели, поражённые ужасом. Что они могли противопоставить таким силам, такой могущественной рати? Архимед пустил в ход свои машины. Сухопутная армия была поражена градом метательных снарядов и громадных камней, бросаемых с великою стремительностью. Ничто не могло противостать их удару, они всё низвергали пред собою и вносили смятение в ряды. Что касается флота - то вдруг с высоты стен брёвна опускались, вследствие своего веса и приданной скорости, на суда и топили их. То железные когти и клювы захватывали суда, подымали их на воздух носом вверх, кормою вниз, и потом погружали в воду. А то суда приводились во вращение и, кружась, попадали на подводные камни и утёсы у подножья стен. Большая часть находившихся на судах погибала под ударом. Всякую минуту видели какое-нибудь судно поднятым в воздухе над морем. Страшное зрелище! Судно поворачивается из стороны в сторону, люди валятся, как бы пускаемые из пращи. Опустошённое судно или разбивается о стены, или погружается в море, будучи выпущено машиною.

Марцелл придвинул на большом помосте машину, называвшуюся самбук, по сходству с музыкальным инструментом этого имени. Когда она приближалась к стене и была ещё довольно далеко, Архимед пустил в неё камень весом в десять талантов^*, затем другой, третий. Камни, как бурею несомые, попадали в машину, ударялись в помост и разбивали его. Марцелл, не зная,что делать, поспешил увести флот и дал приказ войску на суше отступить. Был собран совет; порешили, если будет можно, ночью подойти под самые стены. Машины Архимеда с их огромною силою будут - думали - бросать снаряды так, что они пролетят над головами осаждающих, не попадая в них. Но Архимед давно заготовил приспособления на этот случай. Он расположил и такие машины,которых действие сопряжено было с расстоянием и которые почти без перерыва выбрасывали короткие копья. В стенах сделаны были многие дыры, чрез которые действовали на близком расстоянии скорпионы, невидимые неприятелем.

^* (Талант - около 26 кг.)

Достигнув стен, римляне воображали себя в безопасности, но они были под ударами. Камни падали на них сверху, стены - отовсюду пускали в них копья. Они было удалились, но машины слали новые метательные снаряды и поражали отступающих. Много погибло, суда сталкивались между собою, и осаждаемым причинить какой-либо вред было нельзя. Большая часть машин Архимеда была за стенами. Невидимая рука бросала тысячи зол в римлян; они боролись с богами. Сам Марцелл ускользнул от опасности. Подсмеиваясь над своими инженерами, он говорил: "Не перестать ли нам воевать с этим геометром Бриарием^*, который принимает корабли наши за ковши для черпания воды, разбивает самбук и превосходит сторуких мифологических великанов, бросая столько копий за раз". Действительно, население Сиракуз было телом, а Архимед - душою, проводившей все машины в движение. Все другие орудия бездействовали; только его употреблялись и для нападения, и для защиты. Под конец страх римлян сделался так велик, что как только увидят конец верёвки, бревно над стенами, обращаются в бегство, крича: "ещё машина Архимеда против нас!"

^* (Бриарий - мифический сторукий титан.)

Видя это, Марцелл отказался от всякого нападения и исход осады решил предоставить времени".

"Таков был Архимед,- заключает свой рассказ Плутарх,- так сохранил он, насколько от него зависело, непобедимым и себя, и свой город".

При взятии Сиракуз (212 г. до н. э.) Архимед был убит римскими солдатами.

Конечно, в рассказе Плутарха содержится много преувеличений. Но несомненно одно, в этом рассказе отразилось преклонение римлян перед блестящим инженерным искусством Архимеда. Древние ещё более благоговели перед высоким математическим дарованием Архимеда. Тот же Плутарх отмечает:

"В геометрии нет иных таких предложений, которые в такой мере, как архимедовы, соединяли бы великие трудности с простотою и ясностью решений".

"Поэтому нет оснований не верить писанному об Архимеде, что он жил как бы околдованный какою-то домашнего сиреною, постоянною его спутницей, заставлявшей его забывать пищу, питьё, всякие заботы о своём теле. Иногда, приведённый в баню, он чертил пальцем на золе очага геометрические фигуры или проводил линии на умащённом маслом своём теле, подчиняясь страстно владычеству муз. Автор прекрасных открытий, он просил своих родственников поставить на его могиле цилиндр, включающий в себя шар, и подписать отношение их объёмов".

Действительно, математический гецит Архимеда проявился особенно отчётливо в том, что он взялся за решение труднейших проблем своего времени: вычисление площадей криволинейных фигур, вычисление поверхностей и объёмов цилиндра и шара. Эти проблемы приводят его (в сочинении "Эфодикон", открытом в 1906 г.) к установлению основных понятий интегрирования. Архимед был первым из древних, установившим пределы для π (он нашёл, что π заключено между 3 ¹/₇ и 3 ¹⁰/₁₁). Свой математический гений Архимед проявил и в решении механических задач. Его основные достижения: закон рычага и закон Архимеда получены геометрическим методом. Мы можем с полным правом назвать Архимеда родоначальником математической физики. Рассмотрим здесь результаты Архимеда в области статики. Статика Архимеда изложена в трактатах: "О равновесии плоскостей" и "О плавающих телах". Закон рычага содержится в первом трактате. Центральной идеей трактата является понятие центра тяжести. Эмпирические сведения о равновесии тяжёлого тела были известны давно. Ещё египтяне употребляли отвес. Но только у Архимеда мы находим отчётливое представление о такой точке внутри тела, относительно которой уравновешиваются веса всех остальных точек его, так что тело, опёртое в этой точке, будет в равновесии. Первоначальные эмпирические сведения облачаются у Архимеда в форму аксиом-постулатов. Вот основные из этих аксиом:

1. Равные веса, действуя на равных расстояниях от точки опор невесомого стержня, уравновешиваются (рис. 20 А).
   
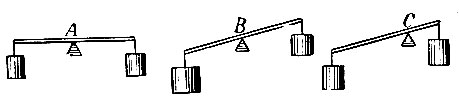
   Рис. 20, А, В, С
   
   
2. При неравных весах, действующих на равных расстояниях от точки опоры невесомого стержня, перевешивает больший (рис. 20 В).
3. Из равных весов, действующих на неравных расстояниях, перевешивает отдалённый (рис. 20 С).
4. Действие одного груза может быть заменено действием нескольких, равномерно распределённых так, что центр тяжести сохраняет неизменное положение. Обратно, несколько равномерно распределённых грузов можно заменить одним, подвешенным в их центре тяжести.
5. У неравных и подобных фигур центры тяжести расположены подобным образом.

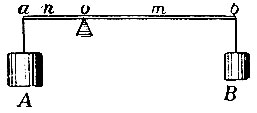
Рис. 21

Исходя из этих постулатов, Архимед доказывает закон рычага следующим образом. Пусть грузы А и В (рис. 21) соизмеримы между собой и относятся, как целые числа:

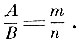
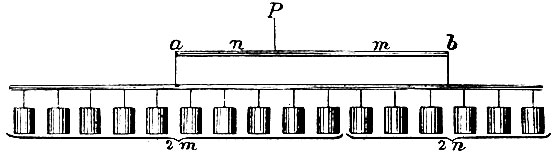
Рис. 22

Пусть, например, m = 5, n = 3. Делим груз А на 2m = 10 равных частей, груз В на 2n = 6 равных частей и распределим их равномерно вдоль невесомого стержня длиной 2(m + n) единиц с точкой опоры Р посредине (рис. 22). По постулату 1 грузы будут в равновесии. Равновесие не нарушится, если 2m грузов соединить в один А, приложенный в их центре тяжести а. Но а отстоит от Р на расстоянии Ра = n единиц, а b отстоит от Р на расстоянии Рb = m единиц. Таким образом, уравновешенные грузы А и В удовлетворяют условию:

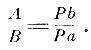
Это и есть закон рычага. Архимед в дальнейшем распространяет его и на случай несоизмеримых грузов. Его доказательство неоднократно подвергалось дискуссии и дальнейшим расширениям.

Обратимся теперь к другому результату Архимеда, к его знаменитому закону. Хорошо известен рассказ Витрувия об обстоятельствах открытия этого закона.

Восклицание Архимеда, открывшего закон в ванне: "Эврика!" (нашёл), стало ходячим выражением. Витрувий рассказывает, что Архимед опытом проверил своё открытие. Конечно, не подлежит сомнению, что опыт натолкнул Архимеда на идею, и опыт дал ему возможность её проверить. Более того, Архимед несомненно умел на опыте определять удельные веса; упоминают даже о поплавке,4с помощью которого сравнивают удельные веса жидкостей (ареометр). Но, верный своему методу, Архимед стремится доказать закон математически, исходя из некоторых постулатов. В основу Архимед кладёт следующую гипотезу о природе жидкости:

"Предполагается, что жидкость по природе своей такова, ч-го при равномерном и непрерывном расположении её частиц менее сдавленная частица вытесняется более сдавленной, и что отдельные частицы этой жидкости испытывают давление отвесно расположенной над ними жидкости, поскольку эта жидкость не замкнута в чём-либо или не испытывает давления со стороны какого-либо другого предмета"^*.

^* (Цитаты взяты из книги "Начала гидростатики" - Архимед, Стевин, Галилей Паскаль, Госуд. технико-теор. издательство.)

Исходя из этой гипотезы, Архимед показывает, что поверхность покоящейся жидкости должна быть сферой, центр которой совпадает с цент ром Земли. В самом деле, если бы этого не было, то не могло бы быть равновесия: одни части жидкости были бы сдавлены больше, чем другие, что согласно постулату привело бы к перемещению менее сдавленных частиц.

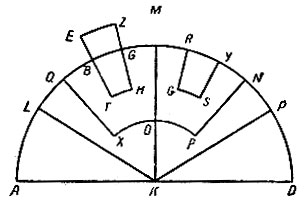
Рис. 23

Эта теорема у Архимеда играет основную роль. Отсюда он доказывает прежде всего, что тела одинакового удельного веса с жидкостью ("имеющие при равном объёме и равный с жидкостью вес") погружаются в жидкость настолько, что совершенно не выступают над её поверхностью, но и не опускаются в ней сколько-нибудь глубже.* Рассмотрим половину "гидросферы" (так для краткости будем называть массу жидкости, заполняющую объём земного шара), ограниченную поверхностью ALMD (рис. 23), и выделим в ней две конические равные части KML и КМР. Из этих конических частей выделим области, ограниченные поверхностями: внешними MQ и МIS и внутренними ХО и ОР. Пусть тело EZTH не погружается сполна в жидкость, а часть EBGZ выетупает над поверхностью. Рассмотрим в смежной области часть RYGS, равную погружённой части тела BGTH. Очевидно, что части жидкости, лежащие на дуге ХО, будут более сдавлены, чем части, лежащие на дуге ОР. Равновесия, согласно основному постулату, не будет. Поэтому тело погрузится как раз настолько, что его поверхность совпадёт с поверхностью гидросферы.

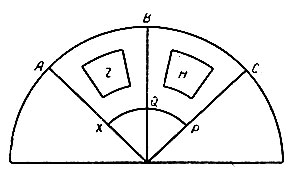
Рис. 24

С помощью той же гидросферы Архимед доказывает, что тело меньшего удельного веса, чем вода, всплывает так, что некоторая часть будет выступать над поверхностью жидкости. В самом деле, если тело Z (рис. 24) погружено в области гидросферы ABXQ, то, выделив в смежной области часть жидкости H, соответствующую Z, находим, что части жидкости, лежащие на дуге QX, будут меньше сдавлены, чем части на дуге QP, что приведёт к нарушению равновесия. Равновесие восстановится тогда, когда тело всплывёт настолько, что недостаток в весе в погружённой части тела будет компенсирован весом выступающей части, так что вес жидкости в объёме погружённой части равен весу всего тела.

Далее, Архимед в следующих двух предложениях утверждает свой закон:

"Предложение VI. Твёрдые тела, которые легче жидкости, будучи погружены в жидкость, стремятся кверху с силой, равной превышению веса жидкости, взятой в объёме этих тел, над весом самих тел.

Предложение VII. Тела, которые тяжелее жидкости, будучи опущены в жидкость, погружаются всё глубже,,пока не достигают дна, и, пребывая в жидкости, теряют в своём весе столько, сколько весит жидкость, взятая в объёме этих тел".

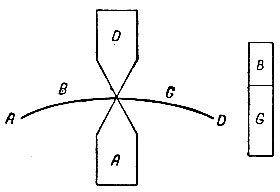
Рис. 25

Предложение VI доказывается так. Пусть В - вес тела А (рис. 25)? B + G - вес жидкости в объёме, равном объёму тела А. Присоединим к А тело D, вес которого равен G. Сумма этих тел будет легче жидкости, взятой в объёме A + D. Поэтому, по предыдущему, тело A + D будет всплывать до тех пор, пока вес выступающей части не компенсирует недостаток в весе погружённой части. Очевидно, равновесие наступит тогда, когда погружённой частью будет А, а выступающей D. А это и доказывает предложение.

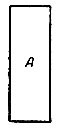
Рис. 26

Предложение VII доказывается на основе предыдущего. Пусть вес тела А равен B + G (рис. 26, 27), а вес жидкости в объёме А равен В. Пусть D - тело легче жидкости и пусть вес его В, а вес жидкости в объёме D равен B + G. Соединим тела А и D вместе. Тогда комбинация обоих тел останется в жидкости в равновесии, не погружаясь, не поднимаясь. В самом деле, объём тел равен A + D, а вес их (B + G) + B. Но таков же вес жидкости в объёме A + D. Но тело D, по предыдущему, стремится вверх с силой, равной G. Таким образом, потеря веса тела А в жидкости равна В (тело падает вниз с той же силой G, с какой его тянет вверх D). Но В это и есть вес жидкости в объёме тела.

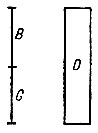
Рис. 27

Таковы доказательства Архимеда. Они просты и глубоки. В лице Архимеда механика древних достигла кульминационного пункта. К его результатам последующие авторы не прибавили нового^*, а в средние века они были утрачены, и архимедово учение о плавании тел было заменено учением схоластов о том, что плавание тел обусловлено их формой.

^* (Исключение составляют исследования Паппа о центре тяжести.)

Как увидим в своём месте, Галилею пришлось восстанавливать в правах Архимеда в спорах с схоластами.

Информация о стали aisi 316ti.