"О сохранении силы" Гельмгольца

Остановимся на сочинении Гельмгольца "О сохранении силы" которое так же не было принято Поггендорфом, как и первые работы Майера. Некоторая метафизичность исходных положений сочинения объясняется самим автором влиянием Канта. Гельмгольц, так же как и Майер, начинает с вопроса о теоретической цели естествознания и усматривает её в открытии "последних неизменных причин природы". Рассматривая материальный мир в духе Босковича - Канта разложенным на течки, взаимодействующие друг с другом по линии, их соединяющей, причём величина взаимодействия зависит от расстояния, Гельмгольц конкретизирует цель теоретических наук о природе так: "Таким образом, окончательно задача физических наук о природе заключается в том, чтобы явления природы свести к неизменным притягательным и отталкивательным силам, величина которых зависит от расстояния".

Приняв в качестве постулата центральные силы как последнюю неизменную причину, Гельмгольц доказывает консервативный характер этих сил.

"Во всех случаях движения материальных точек под влиянием их притягательных и отталкивательных сил, интенсивность которых зависит только от расстояния, потеря в количестве силы напряжения всегда равна приращению живой силы, а приращение первой - потере второй. Следовательно, сумма всех сил и сил напряжения является всегда величиной постоянной".

Сила напряжения на современном языке - потенциальная энергия. Если величина силы в какой-либо точке пути равна φ, то сила напряжения при перемещении точки воздействия от некоторой точки r до точки R, где r и R - расстояния начальной и конечной точек, от неподвижного начала равна 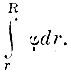Живая сила у Гельмгольца измеряется ¹/₂ mv² (у Майера, Лейбница просто mv²). Таким образом, математическая формулировка принципа принимает вид

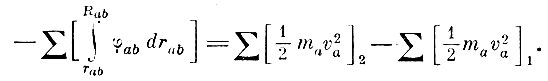
Что для центральных сил справедлив закон сохранения энергии, это знал ещё и Ньютон (см.VIII гл.). Но Гельмгольц связал консервативность этих сил с невозможностью perpetuum mobile.

"Представим себе систему точек, взаимодействия которых определяются их конфигурацией (взаимным расположением и массами). Если мы переведём эту систему из данного начального расположения в другое, то затратим работу, которая будет определяться только конечной и начальной конфигурацией и не будет зависеть от способа перехода. Если бы было справедливо обратное, то, вернувшись в исходное положение, мы получили бы выигрыш или потерю работы без изменения в окружающей обстановке, что и означало бы возможность perpetuum mobile".

Гельмгольц резюмирует свои результаты так:

1. @Всякий раз, когда тела природы действуют друг на друга под влиянием притягательных или отталкивательных сил, не зависящих ни от времени, ни от скорости, сумма сил напряжения и живых сил в системе должна оставаться постоянной, и, следовательно, максимум работы, которая может быть получена, является величиной определённой, конечной".
2. "Если же между телами действуют силы, зависящие от скоростей и времени или действующие по направлениям, не совпадающим с прямыми, соединяющими попарно деятельные материальные точки, например силы вращательные, то возможны такие сочетания этих тел, при которых сила либо теряется, либо выигрывается до бесконечности".
3. "...Если бы... существовали другие силы, кроме центральных, то можно было бы создавать такие прочные соединения тел природы, которые двигались бы сами собою, не нуждаясь в какой-либо связи с другими телами".

Совершенно справедливо, что если силы, действующие в системе, центральные, то система не даёт возможности получить неограниченное количество работы. Но обратное предположение, что из невозможности perpetuum mobile с необходимостью вытекает центральный характер сил, не верно. Принцип невозможности perpetuum mobile является очень широким и суживать его область применения центральными силами, как это сделал Гельмгольц, было бы нецелесообразно. Это впоследствии признал и сам Гельмгольц, сделав соответствующие примечания и дополнения к своей работе.

В таком математическом подходе к вопросу трудно найти первичные побуждения. Но автор сам впоследствии (1891) сообщил об этих побуждениях. Занимаясь у И. Мюллера физиологией, Гельмгольц заинтересовался глубокой проблемой о сущности жизненной силы. "Большинство физиологов,- вспоминает он,- признавали тогда взгляды Ж. Е. Шталя, что в живом организме действуют, правда, физические и химические силы органических веществ, но что в то же время в нем живёт душа жизни, или жизненная сила, которая регулирует проявления физических и химических сил, и что свободное, ничем не регулируемое проявление последних после смерти вызывает гниение...

В этом объяснении я подозревал нечто противоестественное, но мне стоило большого труда вылить это подозрение в форму точного вопроса. Наконец, в последний год моего студенчества я нашёл, что по теории Шталя каждый живущий организм представляет perpetuum mobile". Гельмгольцу были известны работы математиков XVIII в. на тему о возможности perpetuum mobile, и он смог сформулировать проблему: "Какие соотношения должны существовать между различными силами природы, если никакое вообще perpetuum mobile невозможно? Существуют ли на самом деле все эти соотношения?" В этом и состояла цель работы. Гельмгольц описывает далее, как была принята его работа.

"К моему удивлению, авторитеты по физике, с которыми я вступил в сношение, отнеслись к делу совершенно иначе. Они склонны были отрицать самый закон и в усердной борьбе против гегелевской натурфилософии, которую они тогда вели, объявить и мою работу фантастической спекуляцией. Только математик Якоби признал связь между моими мыслями и рассуждениями математиков прошлого столетия, заинтересовался моей попыткой и защищал её от превратного толкования... О работах Джоуля на ту же тему я тогда знал очень мало, о работах же Майера не знал ничего".

Итак, отправляясь от основного вопроса физиологии, Гельмгольц связал его с идеями механиков XVIII в. и, таким образом, пришёл к мысли, что все силы природы можно свести к механическим. Механическая работа является мерой механической "силы". Эта практическая мера известна Гельмгольцу, и поэтому он рекомендует "принимать величину У2 mv2 за количество живой силы, благодаря чему она становится тождественной с мерой величины работы.

Механический подход Гельмгольца, который он сам был вынужден признать узким, представлял шаг назад по отношению к идеям Майера. Но он дал возможность установить абсолютную меру для "живой силы" и рассматривать всевозможные формы энергии либо в виде кинетической ("живых сил"), либо потенциальной ("сил напряжения").

Далее Гельмгольц рассматривает частные случаи. Механика, поскольку отсутствуют силы трения, даёт первый пример приложимости принципа. Сюда относится закон тяготения, движения несжимаемых жидкостей и газов, идеально упругих. Сюда же можно отнести акустику и оптику, если отсутствует абсорбция.

Если при наличии трения или абсорбции имеет место потеря живых сил, то это должно повлечь за собой соответствующую компенсацию в виде появления других форм сил, по преимуществу теплоты. Гельмгольц доказывает несостоятельность флюидной теории тепла и приходит к выводу, что "количество теплоты, содержащейся в теле, может быть рассматриваемо как сумма живой силы теплового движения (свободная теплота) и количества той силы напряжения в атомах, которая при изменении их расположения может вызвать тепловое движение (скрытая теплота, внутренняя работа)".

Касаясь возникновения тепла при химических реакциях, Гельмгольц указывает, что закон Гесса является частным случаем принципа (независимость изменения энергии от формы пути).

Особенно подробно Гельмгольц разбирает электрические и магнитные явления. Ссылаясь на Гаусса и введённую им потенциальную функцию, Гельмгольц выводит выражение энергии в случае электростатических и магнитостатических взаимодействий. Электростатическая энергия составляется из энергии взаимодействия и из собственной энергии тел, она равна

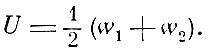
Гельмгольц находит выражение энергии конденсатора

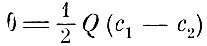
и отсюда количество тепла, выделяющегося в соединительной проволоке при его разряде.

Рассматривая гальваническое электричество, Гельмгольц указывает, что контактная разность потенциалов не должна зависеть от формы и величины соприкасающихся поверхностей, а только от их природы. Отсюда закон Вольта.

Гальванические элементы Гельмгольц делит на три типа: элементы без поляризации (Даниэля, Грове), элементы с поляризацией, но без химического разложения и элементы при наличии тех и других процессов. В элементах без поляризации имеет место окисление (сгорание) металлов - электродов и растворение окиси в кислоте. Равенство теплоты, выделяемой при химических реакциях, и теплоты, выделяемой током в цепи, и даёт возможность определить электродвижущую силу.

Отсюда вытекает, что все цепи, в которых происходят одинаковые химические процессы, обладают одинаковой электродвижущей силой. В цепях с поляризацией имеют место непостоянные поляризационные токи, исчезающие, когда будет достигнуто равновесие между внешними поляризующими силами и внутренними силами поляризации. Если электроды одинаковы (например платиновые), то по выключении внешних поляризующих сил, при замыкании полюсов возникает вторичный ток деполяризации.

В цепях с поляризацией и химическим разложением имеет место и ток поляризации и ток разложения. В термоэлектрических цепях теплота, возникающая в проводниках, должна равняться полному количеству тепла, поглощаемому в местах спая.

Особенную известность получил вывод Гельмгольца электродвижущей силы индукции. Представим себе, что индукция вызывается движением магнита относительно контура тока. Для взаимодействия магнитов имеет место гауссовская потенциальная функция, и если ток, по Амперу, рассматривать как магнитный листок, то потенциальная энергия тока и магнита может быть выражена функцией JV, где V - потенциал магнита относительно проводника, обтекаемого током, равным единице. При бесконечно-малом перемещении магнита в течение промежутка времени dt силы напряжения, действующие в цепи тока, расходуют энергию aAIdt, где а - механический эквивалент тепла, А - теплота, развиваемая силами, действующими в цепи при прохождении единицы электричества. Эта работа тратится на работу перемещения магнита, равную 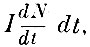и на джоулево тепло в проводниках aI²Wdt, где W - сопротивление цепи.

Таким образом,

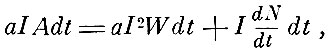
откуда

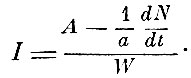
Это и даёт выражение величины э. д. с. индукции

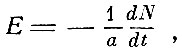
которое совпадает с точностью до множителя с выражением, выведенным Нейманом.

Гельмгольц заканчивает своё исследование следующими словами:

"Изложенным выше, полагаю, мне удалось доказать, что рассматриваемый закон не противоречит ни одному известному явлению в области естествознания, а многими из них он весьма наглядно подтверждается. Я постарался возможно полнее изложить те последствия, которые вытекают из сочетания этого закона с известными до сих пор законами естественных явлений и которые требуют ещё экспериментального подтверждения. Целью настоящего исследования, из-за которого, надеюсь, мне простят его гипотетические части, являлось желание доказать физикам с возможной полнотой теоретическую, практическую и эвристическую важность этого закона, полное подтверждение которого представляет собой, пожалуй, одну из основных задач ближайшего будущего физики".