Опыты Резерфорда по рассеянию α-частиц

В 1906 г. Резерфорд обнаружил рассеяние α-частиц. Метод Резерфорда заключался в следующем. Проволока, покрытая радием С, помещалась в углубление в куске свинца. Над проволокой помещалась узкая щель; α-частицы, проходя через эту щель попадали на фотографическую пластинку. Все это помещалось в латунный цилиндр, из которого выкачивался воздух. Цилиндр помещался между полюсами электромагнита, силовые линии которого шли параллельно проволоке. Получающиеся на фотопластинке полосы были в пустоте резко ограничены. Если же цилиндр заполнялся воздухом, то полосы получались более широкими, а края их размытыми. Если щель прикрыть тонким слоем какого-либо вещества, то полосы уширяются и интенсивность их постепенно убывает от центра к краям.

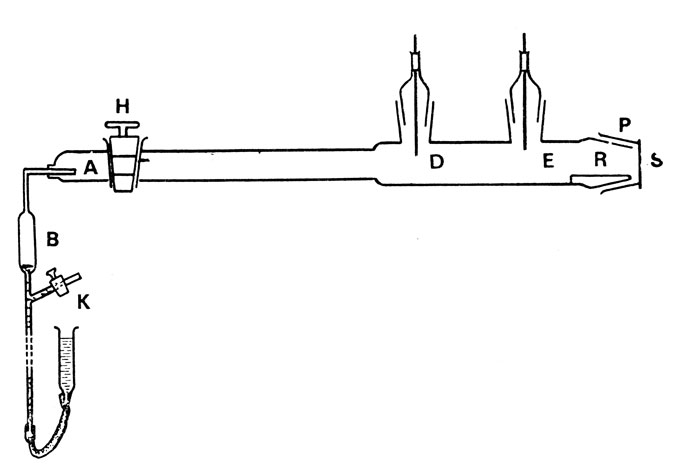
Схема прибора Гейгера по рассеянию α-частиц

В 1909-1910 гг. Г. Гейгер тщательно исследовал рассеяние α-частиц методом сцинтилляции. Прибор Гейгера изображен на рисунке, взятом из статьи Гейгера, 1910 г. В коническую трубку Л, закрытую тонким слоем слюды, вводится радон, который остается в ней на несколько часов. Затем радон засасывается в сосуд В, и вскоре после этого все α-частицы выбрасываются радием: С, осевшим на стенках трубки. Щель D выделяет из потока α-частиц, испускаемых радием С, узкий пучок, который дает яркую картину сцинтилляций на сернистоцинковом экране S. Если затем в Е поместить тонкую пластинку из исследуемого вещества, сцинтилляции на экране уменьшаются вследствие рассеяния α-частиц. Результаты опыта представлены кривыми, где по оси абсцисс отложены углы рассеяния, а по оси ординат - число частиц, рассеиваемых под данным углом. Из опытов Гейгера вытекает, что:

1. Наиболее вероятный угол рассеяния (т. е. угол, для которого число рассеянных частиц наибольшее) возрастает для малых толщин приблизительно пропорционально корню квадратному из толщины вещества, пронизываемого α-частицами. Для больших толщин рассеяние возрастает значительно быстрее.
2. Наиболее вероятный угол, на который отклоняется частица, проходя через атом, пропорционален атомному весу. Действительное значение этого угла в случае золотого атома составляет около ¹/₂₀₀ градуса.
3. Наиболее вероятный угол рассеяния быстро увеличивается с уменьшением скорости α-частицы, будучи в первом приближении обратно пропорциональным кубу скорости.

Наиболее поразительным явлением, наблюдавшимся при рассеянии α-частиц, был факт, открытый в 1909 г. Гейгером и Марсденом, что некоторая малая часть частиц рассеивается на очень большие углы, такие, что частицы вылетают обратно в сторону источника. Для α-частиц, испускаемых радием С, приблизительно одна из 8000 частиц рассеивается на угол, больший прямого.

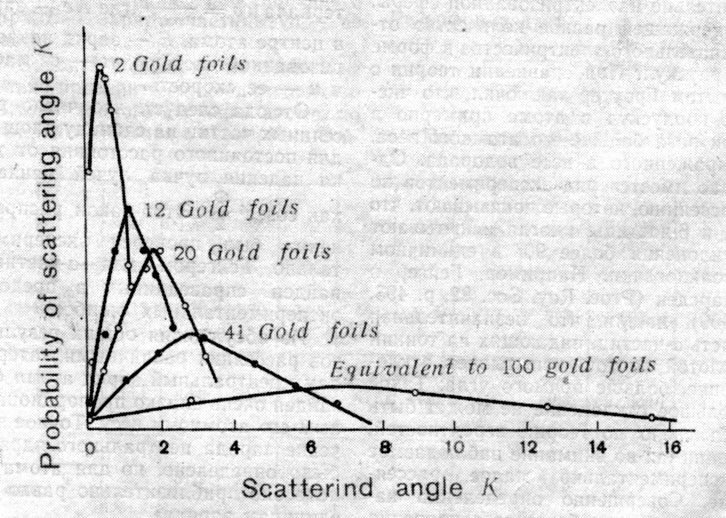
Кривые зависимости угла рассеяния от количества листков золотой фольги

Как объяснить этот факт? Если предположить, что атом имеет структуру, предложенную Д. Д. Томсоном, то единичные отклонения α-частицы при столкновении с таким атомом очень малы, и большие углы рассеяния можно истолковать как кумулятивный эффект, получающийся в результате многих отклонений. Расчеты, проведенные самим Томсоном и Резерфордом, показали, что даже при большем числе столкновений результирующее отклонение α-частицы должно быть очень незначительным. "Я показал,- писал Резерфорд в 1914 г.,- что модель атома, предложенная лордом Кельвином и разработанная с большими деталями сэром Д. Д. Томсоном, не может давать таких больших отклонений, если не принять, что диаметр положительной сферы чрезвычайно мал".

Необходимость интерпретировать результаты опытов Гейгера и Марсдена и привела Резерфорда к ядерной модели атома. Он впервые сообщил о своем открытии в докладе "Рассеяние α- и β-лучей и строение атома", прочитанном в Философском обществе Манчестера 7 марта 1911 г. Мы приведем это сообщение ввиду его огромного исторического значения полностью.

"Хорошо известно, что α- и β-частицы будут отклоняться от своих прямолинейных путей при соударениях с атомами материи. Рассеяние β-частиц вследствие их малого момента (т. е. импульса.- П. К.) и энергии вообще значительно больше, чем отклонение α-частиц. Кажется несомненным, что эти быстро движущиеся частицы действительно проходят через атомную систему и подробное исследование происходящих отклонений должно пролить свет на электрическое строение атома. Обычно предполагается, что наблюдаемое рассеяние является результатом множества малых рассеяний. Сэр Д. Д. Томсон (Proc. Camb. Phil. Soc. 15, p. 5, 1910) недавно продвинул вперед теорию малых рассеяний, и главные выводы теории были экспериментально проверены Гроутером (Proc. Roy. Soc. 84, p. 226, 1910). По этой теории атом предполагается состоящим из положительно наэлектризованной сферы, содержащей равное количество отрицательного электричества в форме корпускул. При сравнении теории с опытом Гроутер заключил, что число корпускул в атоме примерно в три раза больше его атомного веса, выраженного в весе водорода. Однако имеется ряд экспериментов по рассеянию, которые показывают, что α- и β-частицы иногда испытывают отклонения более 90° в единичном столкновении. Например, Гейгер и Марсден (Proc. Roy. Soc. 82, p. 493, 1909) нашли, что незначительная часть α-частиц, падающих на тонкий золотой листок, испытывает отклонение, больше прямого угла. Такое большое отклонение не может быть объяснено по теории вероятностей, принимая во внимание наблюдаемое экспериментально малое рассеяние. Совершенно определенно кажется, что эти большие отклонения происходят в единичном атомном столкновении.

Чтобы объяснить эти и другие результаты необходимо предположить, что наэлектризованные частицы проходят через интенсивное электрическое поле в атоме. Рассеяние заряженных частиц может быть объяснено, если предположить такой атом, который состоит из центрального электрического заряда, сосредоточенного в точке и окруженного однородным сферическим распределением противоположного электричества равной величины. При таком устройстве атома α- и β-частицы, когда они проходят на близком расстоянии от центра атома, испытывают большие отклонения, хотя вероятность большого отклонения мала. По этой теории доля общего числа заряженных частиц, испытывающих отклонение между углами Ф и Ф+dФ дается выражением

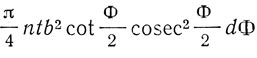
где n число атомов в единице объема рассеивающего материала, t - предполагаемая малой толщина материала и 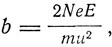где Ne - заряд в центре атома, Е - заряд наэлектризованной частицы, m - ее масса, и u - ее скорость.

Отсюда следует, что число рассеянных частиц на единицу площади для постоянного расстояния от точки падения пучка лучей меняется как cosec^4Ф/₂.Этот закон распределения был проверен экспериментально Гейгером для α-частиц и найден справедливым в пределах экспериментальных ошибок.

Из обсуждения общих результатов рассеяния различными материалами центральный заряд атома был найден очень близко пропорциональным его атомному весу. Точное значение заряда центрального ядра не было определено, но для атома золота оно приблизительно равно 100 единицам заряда".

В такой классически ясной и сжатой форме мир узнал об одном из величайших открытий в истории науки.

Через два года Резерфорд охарактеризовал более подробно свои работы и работы своих сотрудников, приведшие к открытию ядерной модели атома, в книге "Радиоактивные вещества и их излучения".

Здесь были приведены расчеты, позволяющие определить число α-частиц, рассеянных под углом φ к первоначальному направлению пучка:

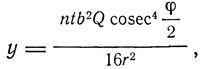
где n - число атомов в единице объема рассеивающего вещества, t - толщина рассеивающей пластинки, Q - число α-частиц, падающих на единицу площади рассеивающей пластинки, r - расстояние от источника до экрана, b - величина, определяемая равенством

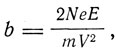
где Ne - заряд рассеивающего ядра, Е - заряд α-частицы, m - ее масса, V - скорость.

Закон Резерфорда позволяет не только проверить справедливость гипотезы ядерного строения атома, но и определить заряд ядра (Ne). Гейгер немедленно в том же, 1911 г. приступил к его проверке. Эксперимент подтвердил справедливость закона cosec^4φ/₂ и дал указание на то, что величина заряда приблизительно пропорциональна атомному весу. В 1913 г. Гейгер и Марсден предприняли новую экспериментальную проверку формулы Резерфорда, пользуясь методом сцинтилляции. "Это была весьма трудная и кропотливая работа, - писал Резерфорд, - так как нужно было сосчитать много тысяч частиц. Результаты Гейгера и Марсдена весьма близко согласуются с теорией".

Вот некоторые данные Гейгера и Марсдена.

При изменении скорости V и прочих неизменных параметрах формула Резерфорда дает, что yV⁴ = const. Данные Гейгера-Марсдена:

¹/_V⁴ (Относительная величина) 1,0 1,21 1,50 1,91 2,84 4,32 9,22

Для зависимости от угла формула Резерфорда дает

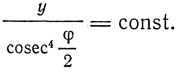
По данным Гейгера и Марсдена,

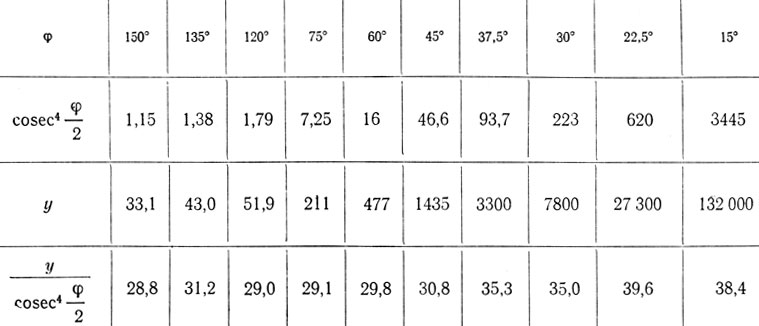
И наконец, для зависимости от заряда (Ne) формула Резерфорда дает постоянство отношений ^v'/_A², где А - атомный вес, v' = ^v/_nt - "приведенное число сцинтилляций". По данным Гейгера и Марсдена,

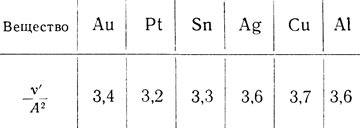
"Гейгер и Марсден нашли,- указывает Резерфорд,- что рассеяние различными атомами вещества приблизительно пропорционально квадрату атомного веса, откуда следует, что заряд атома приблизительно пропорционален атомному весу. Определив число α-частиц, рассеянных тонкими пленками золота, они заключили, что нуклеарный заряд приблизительно равен половине атомного веса, помноженной на заряд электрона. Вследствие трудностей опыта действительное число можно было определить лишь с точностью, не превосходящей 20%.

"Таким образом,- заключает Резерфорд изложение результатов опытов Гейгера и Марсдена,- экспериментальные результаты Гейгера и Марсдена оказались в полном согласии с предсказаниями теории и указали на то, что сделанная мною гипотеза о строении атома, в ее простейших чертах правильна". Интересно отметить, что еще в 1913 г. Резерфорд принимал заряд ядра равным +Ne, т. е. допускал возможность как положительного, так и отрицательного заряда ядра. Действительно, механика отклонения допускает как положительный, так и отрицательный заряд атома. Но целый ряд фактов, и в частности исследования Д. Д. Томсона с положительными лучами, о которых мы вскоре будем говорить, показали, что носители положительного электричества всегда сопряжены с массой, большей или равной массе атома водорода. Массивное ядро может быть носителем только положительных зарядов. Правда, уже в 1913 г. Бор пришел к выводу, что в составе ядра должны быть и электроны. Эта гипотеза была впервые высказана Марией Склодовской-Кюри. Во всяком случае, к 1913 г. окончательно выяснилась связь между зарядом ядра и порядковым номером элемента в менделеевской таблице (ван ден Брук, Мозли).