Глава пятнадцатая. Развитие атомной физики (1918-1925)

Развитие теории Бора. Принцип соответствия

Обратимся теперь к истории изучения электронной оболочки атома. В 1918 г. Бор выступил в Копенгагене с докладом "О квантовой теории линейчатых спектров", в котором сделал существенное дополнение к своей теории в виде так называемого принципа соответствия, или "принципа аналогии", как его иногда называли в то время. Условие частоты Бора не позволяло дать никаких заключений об интенсивности и характере поляризации излучения. В этом отношении оно уступало классической теории излучения, которая представляет движение разложенным на компоненты ряда Фурье, она позволяла вывести совершенно точные заключения об амплитудах и фазах компонент и тем самым об интенсивности и поляризации излучения. Однако, как писал Бор, "оказалось, что существует глубокое соответствие между различными типами возможных переходов от одного стационарного состояния к другому, с одной стороны, и различными гармоническими компонентами разложения - с другой". Бор разбирает случай водородного спектра. Орбита водородного атома определяется соотношениями, которые получаются из классической механики и были даны им еще в первой статье.

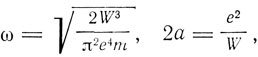
где W - энергия, оцениваемая работой, затрачиваемой на удаление электрона с данной орбиты в бесконечность. Из формулы Бальмера следует, что энергия должна иметь вид

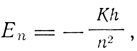
и, подставляя отсюда значения E_n вместо W, получаем

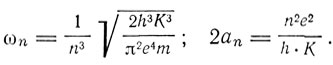
Между частотой обращения по орбите ω_n и частотой излучения υ нет ничего общего. Но для больших квантовых чисел n' и n", несмотря на постоянное значение разности n' - n", отношение ^ω_n'/_ωn" стремится к 1 так, что ω_n' = ω_n" = ω. Частота излучения υ для больших n' и n" представляется формулой

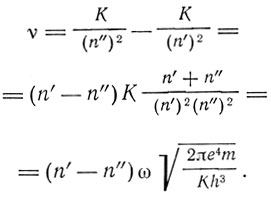
Эта частота совпадает с обертоном разложения:

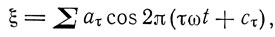
если 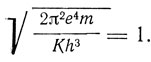Отсюда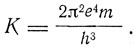

Это значение постоянной Ридберга получается из измерений водородного спектра. "Такое совпадение устанавливает связь между спектром и моделью атома водорода,- пишет Бор.- Если принять во внимание фундаментальное различие между представлениями теории квантов и обычной теорией излучения, то найденная связь становится тем более замечательной".

Н. Бор

Бор указывает, что, хотя в области больших квантовых чисел классическая и квантовые частоты совпадают, механизм излучения в обоих случаях совершенно различен. Тем не менее найденное соответствие позволяет сделать дальнейшие выводы. "Задаваясь вопросом о более глубоком значении найденного соответствия,- пишет Бор,- мы вправе, естественно, ожидать, что соответствие не ограничивается совпадением частот спектральных линий, вычисляемых тем и другим методом, но простирается и на интенсивность. Такое ожидание равносильно тому, что вероятность определенного перехода между двумя стационарными состояниями связана известным образом с амплитудой соответствующей гармонической компоненты".

"Дальнейшее рассмотрение,- продолжает Бор,- приводит нас к тому, что эта своеобразная связь является общим законом переходов между стационарными состояниями; мы должны предположить, что возможность перехода между двумя данными стационарными состояниями связана с наличием определенной гармонической компоненты в движении системы".

Н. Бор в своей лаборатории

Этот принцип, установленный Бором, имел исключительное значение для развития квантовой теории. Но сущность его оставалась совершенно загадочной. Зоммерфельд писал во втором издании своей книги "Строение атома": "Бор нашел в своем принципе соответствия ту волшебную палочку, которая позволяет воспользоваться результатами классической волновой теории для теории квантов для устранения принципиальных противоречий". Принцип соответствия включил в себя и уточнил правило отбора, найденное в том же, 1918 г. А. Рубиновичем. Согласно этому правилу возможны только такие переходы, при которых орбитальный момент количества движения может меняться только на ±^h/_2π и, следовательно, азимутальное квантовое число k только на ±1 (Δk = ± 1), Бор рисовал диаграммы состояний, изображая энергетические состояния точками на параллельных горизонтальных прямых, каждой из которых соответствует свое значение &, так что при переходе от одной горизонтальной прямой к соседней k меняется на 1. Разрешенные переходы изображаются стрелками, соединяющими точки, лежащие на соседних горизонтальных прямых. Состояния в первом горизонтальном ряду (k = 1), который обозначают буквой S, соответствуют переменному члену в "резкой побочной серии", излучаемой при переходе к первому состоянию второй линии Р. В свою очередь, состояния, обозначаемые Р, соответствуют переменному члену "главной серии", излучаемой при переходе из состояния Р к первому состоянию - линии S. Далее идет линия D (k = 3), соответствующая переменному члену "диффузной побочной серии", и т. д. Чертеж Бора соответствует символическим обозначениям серий:

Главная серия

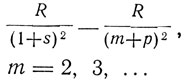
1-я побочная: (диффузная):

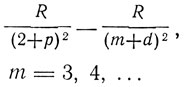
2-я побочная: (резкая):

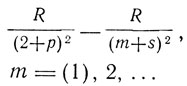
Серия Бергмана:

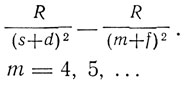
Бор, однако, не пользуется такими обозначениями и предпочитает писать выражение энергетического терма в виде

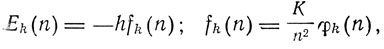
где К - постоянная Ридберга. Принцип соответствия позволяет Бору решить вопрос о поляризационарных соотношениях в случае возмущения атомной системы, вызванного внешним силовым полем. Если возмущенная система допускает разложение на периодические компоненты, то, по принципу соответствия, всякому стационарному движению невозмущенной системы соответствует некоторое число состояний возмущенной системы. Принцип соответствия позволяет понять поляризационные соотношения, наблюдаемые при расщеплении спектральных линий в электрическом поле (эффект Штарка) или в магнитном поле (эффект Зеемана). В последнем случае оказывается, что переходы, для которых k меняется более чем на единицу, невозможны (правило отбора Рубиновича). Рубинович обосновал свое правило, опираясь на закон сохранения механического и электромагнитного импульса при излучении. Эмпирически поляризованная волна, как показал в 1914 г. Абрагам, обладает вращательным импульсом:

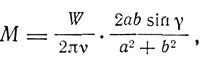
где W - энергия, переносимая волной, поляризованной по эллипсу с полуосями а, b, в единицу времени, γ - разность фаз между взаимно перпендикулярными компонентами^*. Предполагая, что соотношение Абрагама применимо и к атому Бора, Рубинович пишет:

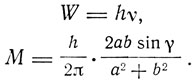
^* (К. Н. Шапошников и Г. Буш в том же, 1914 г. нашли это выражение для волны, поляризованной по кругу, опираясь на исследования А. И. Садовского. В 1915 г. К. Н. Шапошников подробно исследовал вопрос о механических действиях света.)

Но, по Бору, М может меняться только на целое кратное ^h/_2π. Таким образом, при излучении или поглощении энергии атомом вращательный момент меняется по уравнению

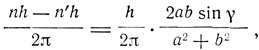
или

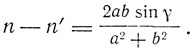
Для волны, поляризованной по кругу a = b, γ = 1, n - n' = 1. Для эллиптически поляризованной, например для a>b,

Так как теория Бора допускает изменение импульса только на целое число ^h/_2π, то n - n' может быть только +1 или 0.

Указывая на этот результат Рубиновича, Бор пишет: "Однако в отношении к системам с радиальной и осевой симметрией можно получить более детальное заключение только при одновременном пользовании принципом соответствия и началом сохранения момента импульса во время процесса излучения. Так, например, в случае атома водорода, возмущаемого центральной силой, на основании начала сохранения момента импульса можно сделать только тот вывод, что при всяком переходе k не может изменяться более чем на единицу, между тем принцип соответствия определенно требует, чтобы при всяком возможном переходе k менялось на 1, и, таким образом, исключается, например, случай неизменности k".

Мы видели, что у Рубиновича Δk = 0 + 1, принцип соответствия же Бора дает только Δk = ± 1. "Кроме того,- продолжает Бор,- принцип соответствия дает не только средство для исключения определенных переходов, как невозможных (в этом смысле принцип соответствия - "принцип отбора"), но и представляет возможность суждения об относительной вероятности различных типов переходов на основании изучения величин амплитуд гармонических колебаний, на которые может быть разложено движение".