Квантовая теория дисперсии

Заметим, что эйнштейновская теория излучения, вводящая коэффициенты, определяющие вероятность излучения и поглощения энергии атомом, уже начала применяться в квантовой теории дисперсии и абсорбции света. Первые шаги в этом направлении были предприняты учеником Рентгена Рудольфом Ладенбургом, который посвятил этому вопросу статью, опубликованную в четвертом томе журнала "Annalen der Physik". Выдвинутые им в этой статье положения были подробно развиты в статье "Абсорбция, рассеяние и дисперсия в Ооровской теории атома", опубликованной в уже неоднократно упоминавшемся нами юбилейном номере "Die Naturwissenschaften" (1923).

Основные положения теории Ладенбурга следующие:

1. Излучение и поглощение света осуществляется согласно постулату Бора в процессе перехода атома из одного квантового состояния в другое. Излучаемая (или поглощаемая) энергия определяется разностью энергии E' и E" в обоих стационарных состояниях, при этом частота излучаемой энергии в соответствии с постулатом Бора равняется:

Процесс абсорбции является полным обращением процесса излучения, и поглощаемая частота в точности равняется частоте, испускаемой при обратном переходе.

2. "Оптические линии поглощения невозбужденного атома соответствуют переходам наиболее слабо связанных электронов атома с нормальной орбиты на высшие возможные орбиты". Далее, возбужденный каким-либо образом атом может при дальнейшем поглощении кванта перейти в еще более высокое квантовое состояние. "Так возникают линии, поглощения возбужденных, и светящихся паров и газов, не принадлежащие к сериям поглощения нормального атома". При этом меняется дисперсия газа. "Эти процессы являются экспериментальным доказательством конечного времени пребывания атома в возбужденном состоянии и тем самым первого постулата Бора". "Опыты по абсобрции и аномальной дисперсии электрически или оптически возбужденных светящихся газов и паров можно истолковать только благодаря воровскому постулату, что атомы и в состоянии с высшей энергией могут находиться конечное время не излучая. Например, в водороде молекула под действие электрического возбуждения расщепляется на атомы, и в то же время электрон переходит во второе квантовое состояние - основное состояние известной серии Бальмера".

3. В вопросе об интенсивности процессов поглощения Ладенбург опирается на результаты Эйнштейна. "При нашем незнании процессов перехода мы при описании этих процессов вынуждены пока принять вместе с Эйнштейном, что они регулируются вероятностными законами". Ладенбург имеет в виду знаменитую работу Эйнштейна 1917 г. о световых квантах. Вместе с Эйнштейном Ладенбург вводит коэффициент а_ki, характеризующий вероятность спонтанного перехода атома из состояния (k) в состояние (/). Далее, вероятность обратного перехода атома из состояния (i) в состояние (k) при поглощении энергии hv характеризуется коэффициентом b_ki ("отрицательное излучение"). Ладенбург усматривает здесь аналогию с поведением классического квазиупругого осциллятора, способность к излучению которого определяется только внутренними свободами отциллятора, подобно тому как коэффициент им зависит только от свойств атомной системы. Точно так же действие внешнего излучения на атом "соответствует тому, что испытывает классический осциллятор под действием внешней волны". Эта важная аналогия связана с принципом соответствия.

4. Методом расчета дисперсии и поглощения у Ладенбурга является введение классических осцилляторов - "электронов дисперсии", которые в совокупности производят такое же действие, как и N квантовых переходов в N атомах. Обозначая число этих электронов дисперсии через N', Ладенбург пишет для энергии, поглощаемой ими в единицу времени в единице объема, коэффициент излучения:

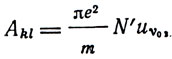
где u_v0 - объемная плотность энергии излучаемой частоты v₀. С другой стороны, если N_i - число атомов в единице объема, находящихся на энергетическом уровне i, то при переходе их на высший уровень k под влиянием энергии падающей волны будет поглощаться энергия:

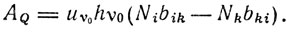
Приравнивая A_kl и A_e, находим

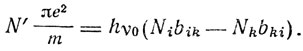
По Эйнштейну, в равновесном состоянии

Далее, согласно Эйнштейну

где g_i и g_k - статистические веса квантовых состояний i и k. Тогда

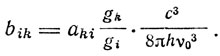
И Ладенбург получает соотношение

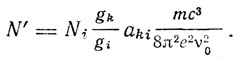
Это число N' электронов дисперсии определяет закон дисперсии:

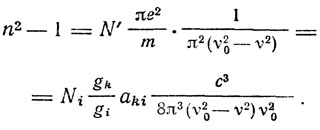
В случае многих резонирующих центров формула Ладенбурга принимает вид

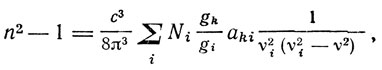
где a_ki - вероятность перехода из высшего состояния k в низшее состояние i, причем низший уровень i может быть и возбужденным.

Суммируя итоги своей теории, Ладенбург и Рейхе подчеркивают, что хотя "мы не знаем механизма, посредством которого падающая волна воздействует на атом" и "не можем описать в деталях реакцию атомов", однако можно думать, что "конечный результат воздействия излучения частоты v на атом не отличается существенно от действия, производимого такой волной на осциллятор". Это действие сострит в том, что "возникают вторичные волны с той же частотой v и в фазе с падающей волной".

Эйнштейн на лекции в Принстоне

Таким образом, классический расчет дает результаты, приближенно согласующиеся с наблюдениями. "Но не всегда!"- подчеркивают авторы. "В предложенном сообщении,- пишут они,- была сделана попытка объяснить эту несостоятельность классической теории на основе атомной теории Бора в духе принципа соответствия. Именно было показано, что количество рассеянной энергии излучения и преломляющая способность, которые классически измерялись числом N' электронов дисперсии, квантовотеоретически определялись величиной вероятности возможных квантовых переходов действительного атома и отношением статистических весов рассматриваемых квантовых состояний".

Сотрудник Бора Гендрик Антони Крамерс развил результаты Ладенбурга и Рейхе. Он не только допустил (это допускали и Ладенбург и Рейхе), что низший уровень i может быть возбужденным, но и учитывал переходы на этот уровень как с высшего уровня k, так и с более низкого уровня j. Формула дисперсии Крамерса в этих предположениях принимает вид ne2N

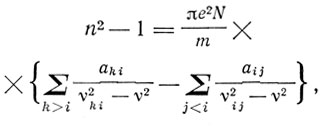
где

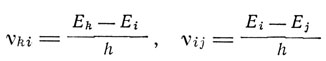
и a_ki, a_ij - эйнштейновские коэффициенты для вероятностей перехода с уровня k на уровень i и с уровня i на уровень j. Это введение Кра-мерсом "отрицательной дисперсии" оказалось оправданным. Сама же формула Крамерса "выходила за рамки качественных следствий принципа соответствия и в действительности представляла результат, который получается из квантовой механики в ее современной форме".