О снежках, орехах, пузырьках и... жидком гелии

Ель в лесу, под елью белка, 
Белка песенки поет 
И орешки все грызет, 
А орешки не простые, 
Все скорлупки золотые, 
Ядра - чистый изумруд,-
 Вот что чудом-то зовут.

(А. С. Пушкин "Сказка о царе Салтане")

Гелий находится почти в самом начале таблицы Менделеева, и тем не менее с момента открытия он доставил физикам массу хлопот необычностью своих свойств. Правда, эти хлопоты с лихвой окупаются красотой и уникальностью явлений, происходящих в жидком гелии, а также теми возможностями, которые он открывает перед исследователями и инженерами для получения очень низких температур. Среди причуд этой квантовой жидкости, наряду со сверхтекучестью^*, стоит и особый, не такой, как в других жидкостях, механизм переноса электрического заряда, о котором мы и расскажем ниже.

^* (См. книгу: Эдельман В. С. Вблизи абсолютного нуля.- М.: Наука, 1983,- Библиотечка "Квант", вып. 26.)

Когда в конце 50-х годов физики только приступали к исследованию этого вопроса, то казалось, что самыми подходящими кандидатами в носители заряда являются электроны и положительные ионы, которые образуются при ионизации гелия. При этом предполагалось, что положительный заряд переносят не непосредственно ионы гелия (они сравнительно тяжелы и трудно разгоняются электрическим полем), а ... дырки. Для того чтобы понять, что такое "дырка", представьте себе, что электрон, находящийся в атоме гелия, в какой-то момент "перепрыгивает" со своего атома на оказавшийся поблизости положительный ион гелия. На его освободившееся место "перепрыгивает" электрон с соседнего атома, на место этого электрона - третий, со следующего атома, и так далее. Со стороны такая чехарда электронов выглядит как движение положительного заряда в противоположную сторону. А так как на самом деле этого положительного заряда нет, а имеет место просто отсутствие очередного электрона на его "рабочем месте", то такой объект называют "дыркой". Этот механизм обычно "работает" в полупроводниках, но представлялось весьма вероятным, что он годится и для жидкого гелия.

Для измерения масс носителей положительного и отрицательного заряда исследовались их траектории в жидком гелии при наложении однородного магнитного поля. Как известно, при попадании заряженной частицы с некоторой начальной скоростью в магнитное поле ее траектория "закручивается" в окружность или спираль. Зная начальную скорость, величину магнитного поля и измерив радиус кругового движения частицы, можно легко определить ее массу. Результаты этих экспериментов оказались весьма неожиданными: массы носителей положительного и отрицательного зарядов в десятки тысяч раз превышали массу свободного электрона!

Конечно, движение электронов и дырок в жидком гелии происходит в окружении атомов, с которыми они взаимодействуют, и поэтому найденные таким образом массы носителей могут отличаться от массы свободного электрона, однако отличаться на пять порядков - это уж слишком! Столь разительное расхождение теоретических расчетов и экспериментальных данных непозволительно даже для необычного гелия. Поэтому необходимо было предложить что-то новое, какой-то до тех пор неизвестный механизм.

Правильное объяснение структуры носителей положительного заряда в жидком гелии вскоре было предложено американским физиком Аткинсом. Известно, что для перевода вещества из жидкого в твердое состояние не обязательно понижать температуру - можно при постоянной температуре повышать давление и этим заставлять вещество затвердевать. То давление, при котором вещество затвердевает, называется давлением затвердевания (Р_тв). Естественно, что величина Р_тв зависит от температуры: чем температура выше, тем труднее путем повышения давления заставить жидкость перейти в твердую фазу, то есть с увеличением температуры Р_тв растет. Оказалось, что вся "хитрость" в структуре носителя положительного заряда заключена именно в сравнительно малом давлении затвердевания жидкого гелия: при достаточно низких температурах Р_тв = 25 атм. Именно этот факт и приводит к весьма необычной структуре носителей положительного заряда в жидком гелии.

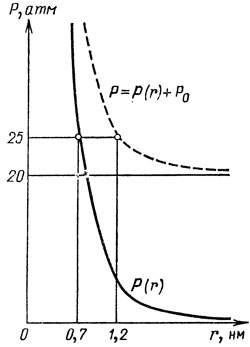
Рис. 1

Мы уже упоминали, что в жидком гелии могут существовать положительные ионы. Взаимодействие такого иона с нейтральным атомом Не приводит к тому, что его электроны чуть-чуть притягиваются к положительному иону, а положительно заряженное ядро атома, наоборот, отталкивается от него. В результате центры положительного и отрицательного зарядов в атоме перестают совпадать и оказываются разнесенными на некоторое расстояние. Таким образом, наличие положительных ионов в жидком гелии приводит к поляризации его атомов. Эти поляризованные атомы притягиваются к положительному иону, что приводит к повышению их концентрации (то есть к появлению избыточной плотности), а следовательно, и к повышению давления по мере приближения к иону. Графически зависимость избыточного давления от расстояния r до положительного иона показана на рис. 1.

Как мы уже говорили, при давлении в 25 атм и низких температурах жидкий гелий затвердевает. Поэтому, как только давление вблизи положительного иона достигнет этого значения, соответствующий объем жидкого гелия вокруг него затвердеет. Из рис. 1 видно, что при малом внешнем давлении затвердевание происходит на расстоянии r₀ = 0,7 нм от иона. Таким образом, положительный ион оказывается как бы "вмерзшим" в "снежок" из твердого гелия. Если мы теперь приложим внешнее электрическое поле, то этот "снежок" начнет двигаться. Однако поскольку он является центром области избыточной плотности атомов гелия, то двигаться в электрическом поле "снежок" будет не один, а в сопровождении "почетного эскорта" - за ним потянется весь "хвост" избыточной плотности. Поэтому полная масса носителя положительного заряда определится суммой трех вкладов. Первый из них - это масса самого "снежка". Она равна произведению плотности твердого гелия на объем "снежка" и при нормальном внешнем давлении составляет 32m₀ (m₀ = 6,7*10^-27 кг - масса атома гелия). Не намного меньшей оказывается и сопровождающая "снежок" "свита" - масса "хвоста" избыточной плотности, которую тащит за собой ион, составляет 28m₀.

Кроме того, при движении тела в жидкости происходит перемещение ее слоев. На это расходуется энергия. Поэтому для того чтобы сообщить телу при его движении в жидкости некоторое ускорение, необходимо приложить к нему большую силу, чем это потребовалось бы в пустоте. Таким образом, в жидкости тело движется так, как если бы его масса была на некоторую величину больше истинной. Эту дополнительную массу, связанную с перемещением слоев жидкости, называют присоединенной^*. Для "снежка", движущегося в жидком гелии при нормальном атмосферном внешнем давлении, присоединенная масса оказывается равной 15m₀.

^* (Мы уже встречались с этим понятием во второй части книги.)

Итак, для полной массы носителя положительного заряда, движущегося в жидком гелии, расчет дает значение 75m₀, что уже хорошо согласуется с величиной, измеренной при эксперименте.

Для объяснения механизма переноса положительного заряда таким образом нам понадобились лишь представления классической физики. Иначе обстоит дело с носителями отрицательного заряда. Прежде всего оказывается, что отрицательно заряженных ионов атома гелия не существует (правда, могут образовываться отрицательные молекулярные ионы Не^-₂, но таких ионов образуется немного, и в переносе заряда главную роль играют не они). Поэтому претендентом в носители отрицательного заряда по-прежнему остается электрон, которому, правда, катастрофически не хватает массы для согласия с экспериментальными данными. Тут-то и приходится столкнуться с причудами квантового мира. Эксперимент показывает, что электрон, которому мы уготовили роль носителя отрицательного заряда в жидком гелии,... не может даже беспрепятственно в него проникнуть.

Для того чтобы в этом разобраться, нам придется сделать небольшое отступление и рассказать об устройстве атомов, имеющих несколько электронов.

В микромире действует важнейший принцип, определяющий поведение коллектива одинаковых частиц. Применительно к электронам его называют принципом Паули. Согласно этому принципу никакие два электрона не могут одновременно находиться в одинаковых квантовых состояниях. Именно принцип Паули объясняет "нелюбовь" атомов гелия к свободным электронам, определяющую те трудности, которые электрону нужно преодолеть, чтобы проникнуть в жидкий гелий.

Энергия электрона в атоме, как мы уже не раз говорили, принимает только определенные квантовые значения. При этом важно, что данному значению энергии может соответствовать несколько различных состояний электрона, отличающихся характером его движения в атоме (например, формой орбиты, а на квантовом языке - устройством облака вероятности, определяющего размазывание электрона в пространстве). Состояния с одинаковым значением энергии образуют оболочку. Согласно принципу Паули с ростом числа электронов в атоме (порядкового номера элемента) они не скапливаются в одинаковых состояниях, а постепенно заполняют все новые оболочки.

Сначала заполняется первая оболочка, отвечающая наименьшей возможной энергии. В ней, вблизи ядра, размещаются только два электрона. Поэтому у гелия, имеющего порядковый номер 2 в таблице Менделеева, первая оболочка оказывается целиком заполненной. Третьему электрону тут уже места нет, и он может расположиться только на достаточном отдалении от ядра. При приближении "лишнего" электрона на расстояние порядка размера атома гелия возникают силы отталкивания, препятствующие дальнейшему сближению.

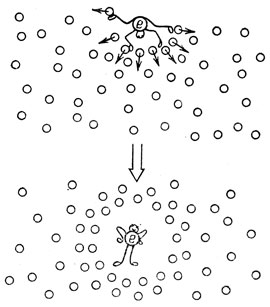
Рис. 2

Таким образом, чтобы загнать электрон в толщу гелия (например, через поверхность), необходимо совершить некоторую "работу входа". Итальянские физики Каррери, Фазоли и Гаэта предположили, что электрон "расталкивает" атомы, к которым он не имеет права приближаться слишком близко, и образует вокруг себя сферически симметричную полость - своеобразный "пузырек" (рис. 2). Такой пузырек вместе с "мечущимся" в нем электроном и является носителем отрицательного заряда в жидком гелии.

Размеры этого пузырька можно оценить. Хоть на близких расстояниях электрон и отталкивается от атомов гелия, однако с увеличением расстояния силы отталкивания быстро падают. В то же время с удаленными атомами Не электрон поступает точно так же, как и положительный ион,- он поляризует их. Поэтому на больших расстояниях взаимодействие электрона с атомами гелия будет таким же, как и в рассмотренном выше случае "снежка". Следовательно, по мере приближения к "пузырьку", в котором "сидит" электрон, избыточное давление в гелии возрастает по тому же закону (см. рис. 1). Однако в случае малого внешнего давления на границе "пузырька" оно еще остается гораздо меньшим 25 атм из-за сравнительно большого его размера. Кроме этого давления, связанного с избыточной плотностью поляризованного гелия, на границе "пузырька" действуют силы поверхностного натяжения, направленные так же, как и силы избыточного давления, к центру "пузырька". Что же уравновешивает эти силы изнутри? Оказывается, противодействие им создает сам электрон.

Действительно, согласно соотношению неопределенностей, о котором мы подробно говорили в специальном разделе, погрешность в измерении импульса электрона связана с неопределенностью в его положении в пространстве соотношением Δp~h/Δx. В рассматриваемом случае положение электрона определяется с точностью до размеров самого "пузырька", то есть Δх~2R. Следовательно, находясь внутри "пузырька", электрон не "сидит на месте", как мы считали выше, а непрерывно "мечется" по нему, обладая импульсом порядка h/2R и, следовательно, кинетической энергией E_k=p²/2me~h²/8m_eR². В результате его соударений со стенками создается некоторое давление (вспомните основное уравнение молекулярно-кинетической теории, связывающее давление газа со средней кинетической энергией хаотического движения его частиц и их концентрацией: P = ₂/₃n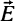_к), которое и компенсирует полное давление на "пузырек" извне. Иными словами, электрон внутри "пузырька" ведет себя подобно газу в закрытом сосуде, но этот газ состоит всего лишь из одной частицы! Концентрация такого газа, очевидно, есть n=1/V=³/₄nR³. Подставляя эту величину и кинетическую энергию Е_к≈h²/8m_eR⁵ в выражение для давления, находим, что P_eπ≈ћ²/4m_eR⁵ (точный квантовомеханический расчет дает для этой величины весьма близкое значение P_eπ≈²ћ²/4m_eR⁵).

Пока внешнее давление мало, то давление на пузырек в основном определяется силами поверхностного натяжения: Р_л = 2σ/R. Приравнивая Р_е = Р_л, находим, что радиус устойчивого пузырька составляет

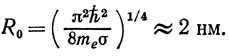
Итак, мы выяснили, что носителями отрицательного заряда в жидком гелии являются "пузырьки" с электронами внутри. Масса таких носителей вычисляется так же, как и масса "снежков". Однако теперь собственной массы "пузырька" практически нет - она равна массе электрона и пренебрежимо мала по сравнению с массой увлекаемой жидкости ("свитой") и присоединенной массой. Поэтому полная масса носителя заряда в жидком гелии определяется лишь присоединенной массой и массой "хвоста" увлекаемой избыточной плотности, которая сопровождает "пузырек" при его движении; из-за большого размера "пузырька" она оказывается значительно больше массы "снежка" и составляет 245m₀.

Теперь рассмотрим, как влияет на свойства носителей зарядов рост внешнего давления Р₀. На рис. 1 показана зависимость полного давления вблизи иона в жидком гелии (с учетом внешнего давления) от расстояния до иона для Р^*₀ = 20 атм. Такая зависимость для произвольного внешнего давления Р₀>25 атм получается переносом зависимости для Р₀=0 вдоль оси ординат. Как видно из рис. 1, чем больше внешнее давление, тем на большем расстоянии от иона полное давление становится равным 25 атм. Поэтому с ростом внешнего давления "снежок" ведет себя подобно настоящему снежному кому, спущенному с горы вниз: он стремительно обрастает "снегом" - твердым гелием, становясь все больше и больше. Зависимость размера снежка r(Р₀) от внешнего давления показана на рис. 3.

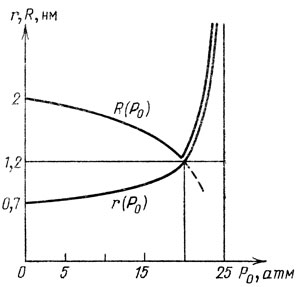
Рис. 3

А как ведет себя "пузырек" с ростом внешнего давления? До поры до времени, подобно любому пузырьку в жидкости, при нарастании внешнего давления он покорно сжимается. Его радиус R(P₀) уменьшается, как это показано на рис. 3. Но вот, при давлении Р^*₀ = 20 атм, графики зависимостей r (Р₀) и R (Р₀) пересекаются - при этом давлении размеры "пузырька" и "снежка" становятся одинаковыми и равными 1,2 нм. Что будет делать "снежок" при дальнейшем увеличении давления, мы знаем - он будет стремительно наращивать свои размеры за счет затвердевающего на его поверхности гелия. А как вести себя "пузырьку" - сжиматься дальше (штриховая линия на рис. 3)? Тут-то "пузырек" и проявляет свой норов - при дальнейшем повышении давления он, подобно "снежку", начинает обрастать ледяной коркой из твердого гелия. Действительно, как это видно из рис. 1, при внешнем давлении Р_*0 = 20 атм полное давление на границе пузырька (на расстоянии 1,2 нм от его центра) становится равным 25 атм, то есть достигает давления затвердевания жидкого гелия. "Пузырек" при этом "одевается в ледяную скорлупу", внутренний радиус которой при дальнейшем повышении давления остается приблизительно неизменным, а внешний в точности равен размеру "снежка" при соответствующем давлении.

Итак, при внешних давлениях больше Р_*0 = 20 атм "пузырьки" обрастают "ледяной скорлупой" и превращаются, таким образом, в некое подобие орехов. Однако ядрышко у этих "орехов" весьма своеобразное - это электрон, который "мечется" внутри скорлупы из твердого гелия.

Остается добавить, что при Р₀→25 атм внешний радиус "ореха", как и "снежка", стремится к бесконечности, что соответствует полному затвердеванию жидкого гелия во всем объеме сосуда. В твердом гелии носителями отрицательного заряда оказываются вмерзшие в него "пузырьки" с размерами, равными внутреннему радиусу бывшего "ореха",- примерно 1,2 нм. Положительный заряд переносят вмерзшие ионы гелия - остатки бывших "снежков". Однако теперь переносить заряды не так-то просто - ведь они находятся в твердом веществе. Поэтому и подвижность этих носителей на много порядков ниже, чем у "снежков" и "пузырьков" в жидком гелии.