Элементы квантовой теории

Квантовая теория исходит из признания двойственной природы частиц (частица - волна). В предыдущей главе мы видели, что во многих случаях свет проявляет волновые свойства, и его длину волны легко измерить. Ньютон (1704) впервые начал рассматривать свет как поток частиц, или корпускул; в дальнейшем такой подход нашел свое отражение в понятии фотон, которое ввел Эйнштейн (1905) для объяснения процесса испускания электронов атомом под действием света. В этом процессе, названном фотоэффектом, свет проявляет свойства частиц, энергия которых зависит от длины световой волны. Подобные корпускулярные свойства обнаруживают все виды электромагнитного излучения. Позднее де Бройлем (1924) была сформулирована и обратная мысль: все объекты, которые обычно ведут себя как частицы, проявляют волновые свойства и характеризуются определенной длиной волны, зависящей от их энергии. Двойственная природа обнаруживается даже у таких относительно больших объектов, как атомы, которые также иногда проявляют волновые свойства.

Существенным моментом квантовой теории является положение о том, что энергия любой системы, проявляющей волновые свойства, может изменяться лишь дискретно определенными элементарными порциями, так называемыми квантами. Энергия кванта прямо пропорциональна частоте соответствующего колебания. Итак, если волна длиной λ распространяется со скоростью v, то ее частота υ (определяемая числом волн проходящих через данную точку в единицу времени), очевидно равна

Например, скорость световых волн составляет около 3*10^8м/_с, а длины волн видимой области спектра около 0,6*10^-6 м, тогда их частота равна 5*10¹⁴ герц (Гц).

Величина кванта энергии для такой волны находится из уравнения

где h - постоянная Планка (названная в честь Макса Планка, который в 1901 г. получил подобное соотношение в другой связи). Эта постоянная весьма мала - 6,6*10^-34Дж/_с. Поэтому дискретный характер изменения энергии заметно проявляется лишь на очень высоких частотах, для которых квант энергии достаточно велик. Кстати, квант света, то есть энергия светового фотона, составляет 3*10^-19 Дж. Изменения энергии такого порядка важны лишь на уровне атома.

До сих пор мы говорили только о понятии энергии в квантовой теории. Теперь рассмотрим другую характеристику частиц - количество движения, или импульс, который определяется как произведение массы частицы на ее скорость mv. В гл. 3, рассматривая кинетическую теорию газов, мы получили соотношение между количеством движения молекул газа и его давлением на стенки сосуда. С помощью чувствительной аппаратуры можно обнаружить давление света^* на освещаемый объект, которое обусловлено наличием у фотонов света импульса. Импульс фотона q связан с его длиной волны следующим соотношением:

^* (Давление света на тела впервые было экспериментально установлено в 1899 г. выдающимся русским физиком П. Н. Лебедевым.- Прим. ред.)

Когда в 1924 г. де Бройль приступил к рассмотрению основных положений квантовой теории, он предположил, что длина волны частицы связана с ее импульсом той же зависимостью, которая характерна для любого вида излучения, то есть соотношением (4.3). В дальнейшем это положение было подтверждено результатами многочисленных экспериментов.

Цель настоящего раздела книги - подготовить читателя к анализу процесса взаимодействия излучения с материальными телами. Для лучшего понимания подобного рода явлений обратимся к простейшей модели атома водорода - модели Бора. В этой модели электроны рассматриваются как классические частицы, которые, вращаясь вокруг ядра, удерживаются на своих орбитах кулоновскими силами электростатического взаимодействия с положительно заряженным ядром. Для поддержания движения частицы по окружности необходимо наличие силы, направленной к центру этой окружности. Если же частица движется без какого-либо воздействия внешней силы, то ее движение, согласно первому закону Ньютона, будет прямолинейным. Легко показать, что при движении со скоростью v по круговой траектории радиуса r частица постоянно испытывает ускорение, равное ^v2/_r и направленное к центру окружности. Как мы знаем из второго закона Ньютона, в этом случае на частицу должна действовать сила, также направленная к центру окружности и пропорциональная ускорению и массе частицы. Сила электростатического взаимодействия электрона с ядром прямо пропорциональна заряду ядра Z и обратно пропорциональна квадрату расстояния между ними. Орбита электрона будет устойчивой, если выполняется соотношение

где C - коэффициент пропорциональности.

Отсюда получаем радиус круговой орбиты электрона

Если импульс электрона равен то, то из уравнения (4.3) мы получаем выражение для длины волны де Бройля:

Согласно этой модели, если поведение электронов не изменяется во времени, то должен существовать ряд длин волн, соответствующих данной круговой орбите, то есть

где π - целое число (1, 2, 3 и т. д.). На основании уравнений (4.5), (4.6) и (4.7) получим

Таким образом, электроны могут находиться только на определенных орбитах, радиусы которых определяются из уравнения (4.8) для каждого n. Далее, каждый электрон обладает кинетической энергией, поскольку он движется, и потенциальной энергией, обусловленной электростатическим взаимодействием с ядром (так как для увеличения расстояния между ними необходимо совершить работу). Можно показать, что полная энергия электрона равна

где A - постоянная, зависящая от выбора положения, при котором потенциальная энергия электрона приравнивается нулю. С учетом уравнения (4. 8) находим

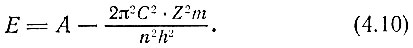
Если в это уравнение последовательно подставлять n (1, 2, 3 и т. д.), мы получим возрастающий ряд значений энергии, которые называются разрешенными энергетическими уровнями электрона. Если электрон характеризуется одним из этих значений энергии, он находится в стационарном состоянии. И покуда электрон остается в атоме, он должен быть в одном из этих состояний.

При переходе электрона с одной орбиты (радиуса r₁) на другую (радиуса r₂) его энергия возрастает на величину

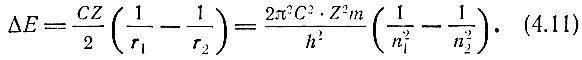
Если переход происходит за счет поглощения излучения, то энергия захваченного фотона должна равняться ΔΕ. Тогда соответствующую энергии такого фотона частоту мы находим из уравнения

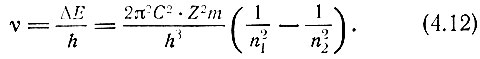
Если какую-либо исходную орбиту электрона охарактеризовать главным квантовым числом n₁, то можно определить спектр частот (и, следовательно, длин волн) излучения, испускаемого при переходе электрона на различные более удаленные орбиты, характеризуемые главными квантовыми числами n2. Очевидно, если энергия поглощаемого фотона выше энергии, необходимой для перехода электрона на самую удаленную орбиту, то электрон покидает атом, что и наблюдается при фотоэлектрическом эффекте.

Итак, чтобы получить представление об энергетических уровнях, о поглощении фотона и т. д., мы воспользовались очень простой моделью атома. Боровская модель достаточно хорошо описывает атом водорода, содержащий лишь один электрон. Для атомов более сложного строения такая модель оказывается слишком упрощенной. Тем не менее теперь мы уже можем приступить к анализу поведения более сложных систем, учитывая при этом, что наши приближения достаточно грубы. В современной квантовой механике отказались от представления об электронах как о частицах, вращающихся вокруг ядра. Однако понятие энергетических уровней, полученное на основе простейших моделей, является существенным элементом и более поздних работ.