Первое начало термодинамики

Машину, предназначенную для получения механической работы, можно схематически представить состоящей из поршня и цилиндра, как показано на рис. 37. Вращение воображаемого выходного вала машины совершается здесь через поступательное движение поршня. Такое устройство называется двигателем. Результаты, полученные при рассмотрении этого простейшего типа двигателей, можно распространить на другие, реальные, двигатели. Для упрощения анализа термодинамического поведения такого двигателя будем считать, что пространство внутри цилиндра заполнено идеальным газом, о котором мы уже говорили в гл. 3. Вещество, содержащееся в пространстве между поршнем и цилиндром двигателя, обычно называют рабочим веществом.

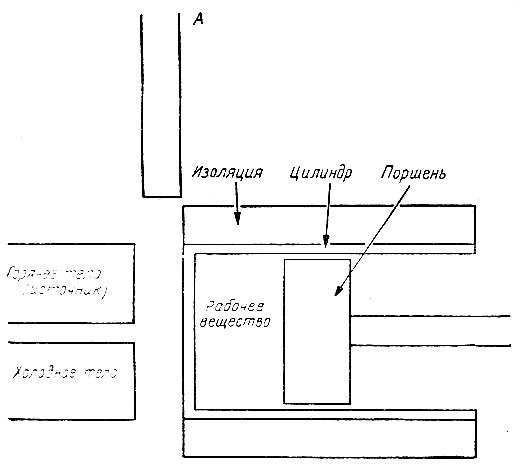
Рис. 37. Простая тепловая машина. А - отдельно показана изоляция цилиндра со стороны торца

Подробно описывать свойства этой среды нет необходимости, мы будем только предполагать, что давление здесь настолько ничтожно, что практически не оказывает сопротивления движению поршня.

Если мы приведем в контакт с цилиндром более нагретое тело, то внутренняя энергия газа увеличивается за счет дополнительной тепловой энергии, полученной цилиндром от тела. Для упрощения предположим, что энергия стенок цилиндра при этом не изменяется. Тогда поступившая на вход системы энергия Q₁ целиком идет на увеличение внутренней энергии газа. Если приращение внутренней энергии мы обозначим через ΔU₁, то получим соотношение

Согласно нашим представлениям, увеличение внутренней энергии идеального газа приводит к повышению его температуры и, как следствие этого (см. гл. 3) - к увеличению давления. Теперь удалим горячее тело, заменив его теплоизолирующим покрытием, которое препятствует рассеянию тепла из цилиндра. (Такая теплоизолирующая оболочка называется адиабатической.) Под действием увеличившегося давления поршень начинает перемещаться, при этом, он совершает работу и может приводить в движение какой-нибудь механизм. В отсутствие теплопередачи через стенки цилиндра такая работа производится лишь за счет уменьшения внутренней энергии газа. Предположим, поршень перемещается до тех пор, пока внутренняя энергия газа не уменьшится до исходной величины, которую она имела перед нагреванием. Пусть в процессе перемещения поршень совершит некоторую работу W₁. Внутренняя энергия, полученная системой в результате нагревания, полностью преобразуется в работу. Тогда мы можем записать равенство W₁ = ΔU₁ и, следовательно, W₁ = Q₁. (Однако не следует думать, что это предел. Если поршню позволить двигаться, и дальше, то он и дальше будет совершать работу, при этом внутренняя энергия газа упадет ниже первоначального значения.)

Это, казалось бы, противоречит сделанному в начале главы замечанию о том, что система не может вернуться в исходное состояние. Когда внутренняя энергия газа падает до своего первоначального значения, поршень оказывается в положении, отличном от исходного. И для непрерывного получения работы мы должны каждый раз возвращать систему в исходное положение, а затем повторять описанный процесс, то есть система должна совершать определенный цикл. Чтобы вернуть систему в исходное состояние, недостаточно просто переместить поршень обратно, при этом необходимо совершить работу по сжатию газа, в результате чего его внутренняя энергия в конце, процесса окажется больше исходной. Таким образом, мы видим, что вернуть систему в первоначальное состояние не просто. Прежде чем сжимать газ, нужно уменьшить его внутреннюю энергию, то есть понизить его температуру. С этой целью можно, например, удалить теплоизоляцию цилиндра, так чтобы часть энергии ΔU₂ перешла через стенки к другому более холодному телу в виде тепла Q₂ = ΔU₂, причем это количество тепла равно работе, затраченной на возвращение поршня в исходное состояние. Следовательно, W₂ = ΔU₂. Таким образом, количество тепловой энергии, затраченной на весь цикл, равно. Q₁ - Q₂, при этом энергия, полученная в виде работы, составляет W₁ - W₂. Поскольку мы считаем, что внутренняя энергия системы в целом не изменилась, то справедливо соотношение

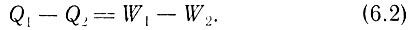
Это уравнение представляет собой одну из форм записи первого начала термодинамики, гласящего, что дли любой системы, совершающей полный цикл, при котором она снова возвращается в первоначальное состояние, затраты тепловой энергии равны совершенной системой работе. В этом случае можно говорить о сохранении энергии. Хотя к подобной мысли пришли давно, но впервые она была сформулирована в 1908 г. Пуанкаре, правда, в несколько ином виде: для любого процесса, в котором системе передается тепло Q, а совершаемая при этом работа равна W, равновесие достигается при изменении внутренней энергии системы

на величину ΔU, которая определяется из соотношения

Это уравнение часто используют в термодинамике как основополагающее для определения внутренней энергии системы, не прибегая к рассмотрению поведения частиц с точки зрения кинетической теории.

На первый взгляд кажется, что в таких процессах теплота ничем не отличается от работы. Напомним, что в 40-х годах прошлого столетия английский физик Джоуль поставил серию экспериментов, в которых определенное повышение температуры, а следовательно, и соответствующее изменение внутренней энергии простой системы было получено как за счет ее нагревания, так и при совершении над ней механической работы. В своих экспериментах, знакомых многим из нас, Джоуль наблюдал повышение температуры при трении, при прохождении электрического тока через цепь с сопротивлением и т. д. В результате была установлена связь между единицами теплоты и работы и введен некий коэффициент пропорциональности, получивший название механического эквивалента теплоты. В настоящее время для измерения и теплоты, и работы пользуются одной и той же единицей, которая называется джоулем. (В этой книге мы будем использовать более удобную и широко известную единицу - 1 кВт*ч = 3,6 МДж.)