АБЕЛЯ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

Расстановка ударений: А`БЕЛЯ ИНТЕГРА`ЛЬНОЕ УРАВНЕ`НИЕ

АБЕЛЯ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ - интегральное ур-ние

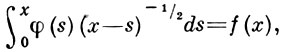
где f(х) - известная ф-ция, φ(х) - искомая ф-ция. Получено и решено Н. Абелем (N. Abel) в 1823 при рассмотрении движения материальной точки в вертик. плоскости под действием силы тяжести. А. и. у. часто возникает при решении т. н. обратных задач, напр. при определении потенц. энергии по периоду колебаний или при восстановлении рассеивающего поля по эффективному сечению в классич. механике. А. и. у. относится к классу Вольтерры уравнений 1-го рода, рассматривают также обобщённое А. и. у.

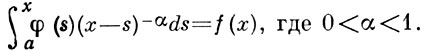
. Если f(х) - непрерывно дифференцируемая ф-ция, то это ур-ние имеет единств, непрерывное решение:

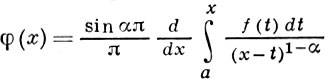
В классе обобщенных функций решение существует при любых α.

Лит.: Гельфанд И. М., Шилов Г. Е., Обобщенные функции и действия над ними, 2 изд., М., 1959; Михлин С. Г., Лекции по линейным интегральным уравнениям. М., 1959.

С. В. Молодцов

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.

силовой медный кабель гибкий четырехжильный