АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ

Расстановка ударений: АБЕРРА`ЦИИ ОПТИ`ЧЕСКИХ СИСТЕ`М

АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ (от лат. aberratio - уклонение, удаление) - искажения изображений, даваемых реальными оптич. системами, заключающиеся в том, что оптич. изображения неточно соответствуют предмету, оказываются размыты (монохроматич. геом. А. о. с.) или окрашены (хроматич. А. о. с.). В большинстве случаев аберрации обоих типов проявляются одновременно.

В приосевой, т. н. параксиальной, области (см. Параксиальный пучок лучей) оптич. система близка к идеальной, т. е. точка изображается точкой, прямая линия прямой и плоскость - плоскостью. Но при конечной ширине пучков и конечном удалении точки- источника от оптич. оси нарушаются правила параксиальной оптики: лучи, испускаемые точкой предмета, пересекаются не в одной точке плоскости изображений, а образуют кружок рассеяния, т. е. изображение искажается - возникают аберрации.

Геом. А. о. с. характеризуют несовершенство оптич. систем в монохроматич. свете. Происхождение А. о. с. можно понять, рассмотрев прохождение лучей через центрированную оптич. систему L (рис. 1). OO₁ - плоскость предмета, O'O'₁ - плоскость изображений, РР₁ и P'P'₁ - соответственно плоскости входного и выходного зрачков. В идеальной оптич. системе все лучи, испускаемые к.-л. точкой С(z, у) предмета, находящейся в меридиональной плоскости (z=0) на расстоянии y=l от оси, пройдя через систему, собрались бы снова в одну точку С'(z'₀, y'₀). В реальной оптич. системе эти лучи пересекают плоскость изображения O'O'₁ в разных точках. При этом координаты z' и y' точки В пересечения луча с плоскостью изображения зависят от направления луча и определяются координатами р_у и p_z точки А пересечения с плоскостью входного зрачка. Отрезок С'В характеризует несовершенство изображения, даваемого данной оптич. системой. Проекции этого отрезка на оси координат равны δg=y'-y'₀ и δG=z'-z₀ и характеризуют поперечную аберрацию. В заданной оптич. системе δg' и δG' являются ф-циями координат падающего луча СА: δg'=f₁(l, p_y, p_z) и δG'=f₂(l, p_y, p_z). Считая координаты малыми, можно разложить эти ф-ции в ряды по p_у, p_z и l.

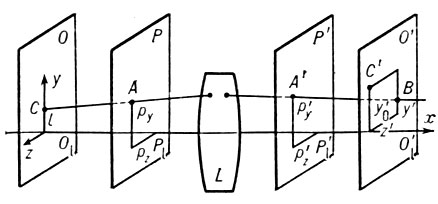
Рис.1

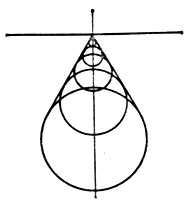
Рис.2. Кома

Линейные члены этих разложений соответствуют параксиальной оптике, следовательно коэфф. при них должны быть равными нулю; чётные степени не войдут в разложение ввиду симметричности оптич. системы; т. о. остаются нечётные степени, начиная с третьей; аберрации 5-го порядка (и выше) обычно не рассматривают, поэтому первичные А. о. с. наз. аберрациями 3-го порядка. После упрощений получаются след. ф-лы

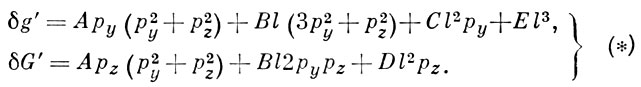
Коэфф. А, В, С, D, E зависят от характеристик оптич. системы (радиусов кривизны, расстояний между оптич. поверхностями, показателей преломления). Обычно классификацию А. о. с. проводят, рассматривая каждое слагаемое в отдельности, полагая др. коэфф. равными нулю. При этом для наглядности представления об аберрации рассматривают семейство лучей, исходящих из точки-объекта и пересекающих плоскость входного зрачка по окружности радиуса ρ с центром на оси. Ей соответствует определённая кривая в плоскости изображений, а семейству концентрич. окружностей в плоскости входного зрачка радиусов ρ, 2ρ, 3ρ и т. д. соответствует семейство кривых в плоскости изображений. По расположению этих кривых можно судить о распределении освещённости в пятне рассеяния, вызываемом аберрацией.

Сферическая аберрация соответствует случаю, когда А≠0, а все др. коэфф. равны нулю. Из выражения (*) следует, что эта аберрация не зависит от положения точки С в плоскости объекта, а зависит только от координаты точки А в плоскости входного зрачка, а именно, пропорциональна ρ³. Распределение освещённости в пятне рассеяния таково, что в центре получается острый максимум при быстром уменьшении освещённости к краю пятна. Сферич. аберрация - единств, геом. аберрация, остающаяся и в том случае, если точка- объект находится на гл. оптич. оси системы.

Кома определяется выражениями при коэфф. В≠0. Равномерно нанесённым на входном зрачке окружностям соответствуют в плоскости изображения семейства окружностей (рис. 2) с радиусами, увеличивающимися как ρ², центры к-рых удаляются от параксиального изображения также пропорционально ρ². Огибающей этих окружностей (каустикой) являются две прямые, составляющие угол 60°. Изображение точки при наличии комы имеет вид несимметрич. пятна, освещённость к-рого максимальна у вершины фигуры рассеяния и вблизи каустики. Кома отсутствует на оси центрированных оптич. систем.

Астигматизм и кривизна поля соответствуют случаю, когда не равны нулю коэфф. С и D. Из выражения (*) следует, что эти аберрации пропорциональны квадрату удаления точки-объекта от оси и первой степени радиуса отверстия. Астигматизм обусловлен неодинаковой кривизной оптич. поверхности в разных плоскостях сечения и проявляется в том, что волновой фронт деформируется при прохождении оптич. системы, и фокус светового пучка в разных сечениях оказывается в разных точках. Фигура рассеяния представляет собой семейство эллипсов с равномерным распределением освещённости. Существуют две плоскости - меридиональная и перпендикулярная ей сагиттальная, в к-рых эллипсы превращаются в прямые отрезки. Центры кривизны в обоих сечениях наз. фокусами, а расстояние между ними является мерой астигматизма.

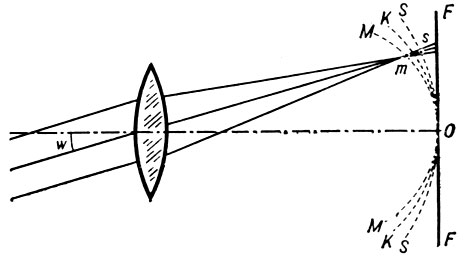
Рис.3. Астигматизм

Пучок параллельных лучей, падающих на оптич. систему под углом w (рис. 3), в меридиональном сечении имеет фокус в точке m, а в сагиттальном - в точке s. С изменением угла w положения фокусов m и s меняются, причём геом. места этих точек представляют собой поверхность вращения MOM и SOS вокруг гл. оси системы. На поверхности КОК, находящейся на равных расстояниях от MOM и SOS искажение наименьшее, поэтому поверхность КОК наз. поверхностью наилучшей фокусировки. Отклонение этой поверхности от плоскости представляет собой аберрацию, наз. кривизной поля. В оптич системе может отсутствовать астигматизм (напр., если MOM и SOS совпадают), но кривизна поля остаётся: изображение будет резким на поверхности КОК, a в фокальной плоскости FF изображение точки будет иметь вид кружка.

Дисторсия проявляется в случае, если E≠0 как видно из ф-л (*), она может быть в меридиональной плоскости: δg'=El³; δG'=0. Дисторсия не зависит от координат точки пересечения луча с плоскостью входного зрачка (поэтому каждая точка изображается точкой), но зависит от расстояния точки до оптич. оси (∼l³), поэтому изображение искажается, нарушается закон подобия. Напр., изображение квадрат; имеет вид подушкообразной и бочкообразной фигур (рис. 4) соответственно в случае E>0 и E<0.

Труднее всего устранить сферич. аберрацию и кому. Уменьшая диафрагму, можно было бы практически полностью устранить обе эти аберрации, однако уменьшение диафрагмы уменьшает яркость изображения и увеличивает дифракц. ошибки.

Рис.4. Дисторсия

Подбором линз устраняют дисторсию, астигматизм и кривизну поля изображения.

Хроматич. аберрации. Излучение обычных источников света обладает сложным спектральным составом, что приводит к возникновению хроматич. аберраций. В отличие от геометрических, хроматич. аберрации возникают и в параксиальной области. Дисперсия света порождает два вида хроматич. аберраций: хроматизм положения фокусов и хроматизм увеличения. Первая характеризуется смещением плоскости изображения для разных длин волн, вторая — изменением поперечного увеличения. Подробнее см. Хроматическая аберрация.

Лит.: Слюсарев Г. Г., Методы расчета оптических систем, 2 изд., Л., 1969; Сивухин Д. В., Общий курс физики, [т. 4] — Оптика, 2 изд., М., 1985; Теория оптитческих систем, 2 изд., М., 1981.

Г. Г. Слюсарев

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.