АВТОМОДЕЛЬНАЯ АСИМПТОТИКА

Расстановка ударений: АВТОМОДЕ`ЛЬНАЯ АСИМПТО`ТИКА

АВТОМОДЕЛЬНАЯ АСИМПТОТИКА в квантовой теории поля — независимость асимптотич. формы амплитуд и сечений процессов взаимодействия элементарных частиц при высоких энергиях и больших передачах импульса (глубоко неупругих процессов, инклюзивных и эксклюзивных процессов, адронадронных взаимодействий) от размерных динамич. параметров, таких как массы частиц, эфф. радиус сильного взаимодействия и др. Единств, переменными, от к-рых зависит А. а., являются безразмерные отношения больших кинематич. инвариантов, характеризующих рассматриваемый процесс (не меняющиеся при выборе единиц измерения энергии и импульса частиц), т.е. автомодельное асимптотич. поведение тесно связано с масштабной инвариантностью при высоких энергиях. Автомодельное поведение в физике высоких энергий находится в близкой аналогии со свойством подобия или самоподобия (автомодельности) в задачах газо- и гидродинамики (см. Автомодельное течение), откуда и был заимствован термин (см. также Автомодельность).

Сформулированный в 1969 принцип автомодельности в физике элементарных частиц [1], определяющий наиб, общую форму А. а. амплитуд и сечений процессов, позволяет, опираясь лишь на законы физ. подобия и анализ размерностей, прогнозировать поведение наблюдаемых характеристик процессов взаимодействия лептонов и адронов с адронами при предельно высоких энергиях. Напр., для процесса глубоко неупругого взаимодействия, в к-ром адрону с 4-импульсом р передаётся от лептона большой 4-импульс q, в т. н. бьёркеновском пределе [2] q² ∼ υ = 2pq >> p² = m² (m — масса адрона; используется система единиц, в к-рой c=1) при фиксированных значениях безразмерного отношения больших кинематич. инвариантов ^υ/_q² структурные функции F(q², υ) имеют в соответствии с принципом автомодельности следующий наиб, общий вид:

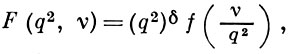
где показатель степени δ определяется физической размерностью структурной ф-ции, а f — произвольная ф-ция [1].

На основе принципа автомодельности было также предсказано поведение сечений процесса образования мюонных пар (μ⁺, μ,^-)в адронных столкновениях в области больших передач 4-импульса [3].

В квантовой теории поля А. а. при больших передачах импульса связывается с локальными свойствами взаимодействия частиц на малых расстояниях. Строгое обоснование непротиворечивости А. а. и их взаимнооднозначная связь с характером сингулярности произведений двух локальных токов j_μ(x) j_μ(x') (х, х' - пространственно-временные точки, μ=0, 1, 2, 3) на световом конусе [т. е. при (х—х')²=0] на основе общих принципов квантовой теории поля, таких как локальность, причинность, спектральность и др. (см. Аксиоматическая квантовая теория поля), даны в работах [4]. Однако в теории с асимптотической свободой (напр., в квантовой хромодинамике, в моделях великого объединения) А. а. нарушается множителями, логарифмически зависящими от q².

Гипотеза автомодельности и учёт кварковой структуры адронов привели в 1973 к формулировке кваркового счёта правил, определяющих скорость степенного убывания амплитуд и сечений различных эксклюзивных процессов при больших передачах импульсов в зависимости от кваркового содержания участвующих в этих процессах частиц.

Лит.: 1) Матвеев В. А., Мурадян Р. М., Тавхелидзе А. Н., Об автомодельном характере асимптотического поведения формфакторов электромагнитных и слабых процессов, [Дубна, 1969]; 2) Вjогken I. D., Lecture in Varenna School, Course 41, 1967; 3) Матвеев В. А., Мурадян Р. М., Тавхелидзе А. Н., Автомодельность, коммутаторы токов и векторная доминантность в глубоко неупругих лептон-адронных взаимодействиях, в кн.: Проблемы физики элементарных частиц и атомного ядра, т. 2, в. J.М., 1971; 4) Боголюбовы. Н., Владимиров В. С., Тавхелидзе А. Н., Об автомодельной асимптотике в квантовой теории поля II, «ТМФ», 1972, т. 12, № 3, с. 305.

В. А. Матвеев

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.