АВТОМОДЕЛЬНОЕ ТЕЧЕНИЕ

Расстановка ударений: АВТОМОДЕ`ЛЬНОЕ ТЕЧЕ`НИЕ

АВТОМОДЕЛЬНОЕ ТЕЧЕНИЕ — течение жидкости (газа), к-рое остаётся механически подобным самому себе при изменении одного или неск. параметров, определяющих это течение. В механически подобных явлениях наряду с пропорциональностью геом. размеров соблюдается пропорциональность механич. величин — скоростей, давлений, сил и т. д. (см. Подобия теория).

А. т. — частный случай течения жидкости (газа), когда общая задача гидроаэромеханики сводится к системе безразмерных обыкновенных дифференц. ур-ний и граничных условий, зависящих от одной надлежащим образом выбранной безразмерной независимой переменной. Благодаря этому задача расчёта течения упрощается, и удаётся получить её численное, а в ряде случаев и аналитич. решение.

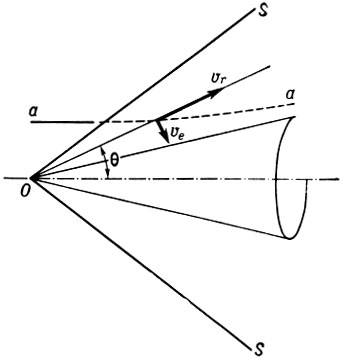
Рис.1. Обтекание бесконечного конуса равномерным сверхзвуковым потоком идеального газа; OS — коническая ударная волна, аα — линия тока

Так, при обтекании бесконечного конуса сверхзвуковым равномерным потоком идеального газа (рис. 1) нельзя выделить характерный линейный размер, поэтому при растяжении или сжатии картины течения относительно вершины конуса О в произвольное число раз картина не изменяется, т. е. остаётся подобной самой себе. Все безразмерные характеристики течения — относит, скорости, давления и т. д. зависят от одной независимой геом. переменной — полярного угла θ . Обтекание конуса описывается системой из двух ур-ний — с граничными условиями на поверхности конуса и на присоединённой конич. ударной волне:

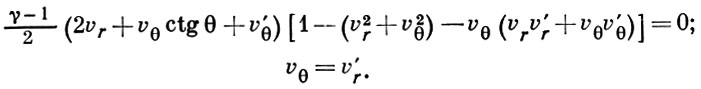
Здесь υ_r, υ_θ — составляющие относит, скорости в полярной системе координат r, θ, γ=^c_p/_cV, — отношение уд. теплоёмкостей.

А. т. в ламинарном пограничном слое существуют лишь при нек-рых спец. законах изменения скорости U вне пограничного слоя, в частности при постоянной скорости U=const (пограничный слой на продольно обтекаемой бесконечной плоской пластине). Т. к. в рассматриваемом течении нет к.-л. характерной длины, то профили скорости v в автомодельном пограничном слое в разл. поперечных сечениях x=const подобны друг другу и в безразмерных переменных представляются универсальной ф-цией ^υ/_U=φ(^y/_δ), где y - расстояние по нормали к пластине, δ — толщина пограничного слоя. Безразмерная ф-ция тока f(η) в автомодельном пограничном слое удовлетворяет обыкновенному дифференц. ур-нию

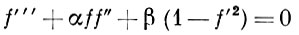
с граничными условиями f=0, f'=0 при η=0 и f'=1 при η=∞. Здесь α, β — нек-рые постоянные, a η -безразмерная автомодельная переменная, пропорциональная ^y/_δ. Аналогичные А. т. возможны и в пограничном слое, возникающем при свободной (естественной) конвекции.

А. т. возникает и в осн. участке турбулентной свободной струи (рис. 2), вытекающей из плоского или круглого сопла в неподвижную среду, т. к. в сходственных точках любых двух поперечных сечений безразмерные величины скорости (темп-ры, концентрации) одинаковы.

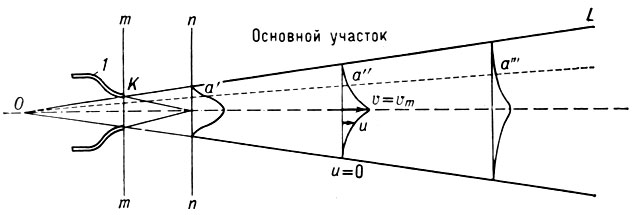
Рис.2. Схема свободной турбулентной струи: О — полюс, 1 — сопло, m — m — сечение среза сопла, n — n — конец начального участка, KL — граница струи, α', α ', α'' — сходственные точки на профилях скорости

Для нестационарных А. т. состояние течения в нек-рый момент времени t, характеризуемое распределением давлений, скоростей, темп-р в пространстве, механически подобно состоянию течения при любом др. значении t. Такие течения образуются, напр., в случае сильного взрыва, а также при распространении в горючей смеси фронта пламени или детонации. В случае сферич. симметрии взрыв (поджигание смеси) происходит в точке, в случае цилиндрич. симметрии — вдоль прямой, а в случае плоских волн — вдоль плоскости. Если в момент t=0 мгновенно выделяется конечная энергия Е₀, а нач. плотность газовой среды равна ρ₁, то введение безразмерной автомодельной переменной

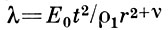
(где r — расстояние от места взрыва, ν=3 — для сферич. волн, ν=2 — для цилиндрических и ν=l —для плоских) позволяет свести задачу определения безразмерных давлений, скоростей, темп-р за взрывной (ударной) волной к решению системы обыкновенных дифференц. ур-ний с автомодельными граничными условиями на ударной волне.

В широком смысле под автомодельностью течения иногда понимают независимость безразмерных параметров, характеризующих течение, от подобия критериев. Так, коэфф. лобового аэродинамич. сопротивления C_X (см. Аэродинамические коэффициенты) можно считать автомодельным по Маха числу М или Рейнолъдса числу Re, если в нек-ром диапазоне их изменения С_X от них не зависит. Автомодельность коэфф. C_X по М и Re существует для большинства тел, обтекаемых газом, при больших М (М>8) или достаточно больших Re (Re>10⁷).

Лит.: Седов Л. И., Методы подобия и размерности в механике, 9 изд., М., 1981; Xеиз У.-Д., Пробстин Р.-Ф., Теория гиперзвуковых течений, пер. с англ., М., 1962; Шли хтинг Г., Теория пограничного слоя, М., 1974.

С. Л. Вишневецкий

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.