
АВТОФАЗИРОВКА
Расстановка ударений: АВТОФАЗИРО`ВКА
АВТОФАЗИРОВКА (фазовая устойчивость) — явление устойчивости движения частиц в продольном (вдоль орбиты) направлении в резонансных ускорителях, обусловленное зависимостью промежутка времени Т между последующими ускорениями от полной энергии ё частицы. Открыто в 1944—45 В. И. Векслером и независимо от него Э. М. Макмилланом (Е. М. McMillan). Лежит в основе действия большинства совр. резонансных ускорителей заряж. частиц.
В простейшем случае циклич. ускорителя с однородным магн. полем период обращения Т связан со значением магн. индукции В на круговой орбите и полной релятивистской энергией частицы ξ соотношением
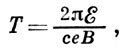 (1)
(1)где е — заряд частицы. Из (1) видно, что с ростом энергии частицы период обращения увеличивается. Обозначим через φ0 «равновесную фазу» — фазу поля (отсчитываемую от его макс, значения; рис. 1) в ускоряющем зазоре, попадая в к-рую частица набирает такую энергию eV0cosφ0 (V0 — ускоряющее напряжение), чтобы непрерывно двигаться в резонанс с ускоряющим полем. Период обращения Т этой частицы равен или кратен периоду ускоряющего поля Tуск, T=qTуск, где q - целое число, наз. кратностью ускорения. Очевидно, фаза - φ0, будет также равновесной, т. к. в этой фазе частица набирает точно такую же энергию, как и в фазе φ0. Если частица попадёт в фазу φ1>φ0, она наберёт энергию eV0cosφ0 меньшую eV0cosφ0, прирост её энергии будет меньше равновесного значения, а следовательно, согласно (1), и период станет меньше равновесного. Поэтому при следующем обороте частица придёт к ускоряющему промежутку раньше, т. е. её фаза приблизится к равновесной. Напротив, немного отставшая частица (φ2<φ0) приобретёт избыточную энергию (т. к. eV0cosφ2>eV0cosφ0), её период обращения станет больше равновесного, вследствие чего на следующем обороте она позже придёт к ускоряющему зазору и её фаза тоже приблизится к равновесной.
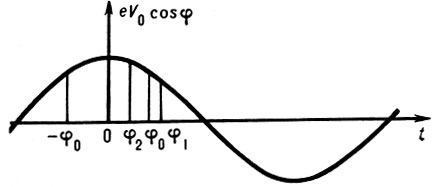
Малые отклонения энергии частицы от равновесной также имеют тенденцию уменьшаться. Действительно, если частица находится в равновесной фазе φ0, но её энергия больше равновесной (соответствующей периоду ускоряющего поля Tуск), то её период обращения больше qTуск и она приходит на след, обороте к зазору с опозданием, т. е. её фаза φ'>φ0, а энергия eV0cosφ'<eV0cоsφ0. Т. о., отличие энергии от равновесной будет уменьшаться.
Благодаря описанному механизму частицы, находящиеся в нек-рой окрестности равновесной фазы φ0 (т. н. область захвата), совершают колебания около этой фазы, т. е. фаза φ0, динамически устойчива. Все частицы, находящиеся в области захвата, колеблясь около фазы φ0, набирают в ср. такую же энергию, как и частица в равновесной фазе (т. н. равновесная частица), т. е. ускоряются.
Аналогично можно показать, что вторая равновесная фаза -φ0, неустойчива: малые отклонения от неё приводят к дальнейшему уходу частиц от этой фазы.
В общем случае для циклич. ускорителей с магн. полем, зависящим от азимута и радиуса, ф-лу (1) следует заменить на соотношение
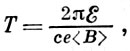
где 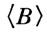 — нек-рое усреднённое по орбите значение магн. индукции, зависящее от энергии частицы; поэтому характер зависимости Т от ξ оказывается более сложным. Если ∂Т/∂ξ>0, т. е. период растёт с ростом энергии, то, как и раньше, оказывается устойчивой равновесная фаза φ0, вблизи к-рой ускоряющее электрич. поле убывает с увеличением времени. Если же ∂Т/∂ξ<0, т. е. период обращения убывает со временем, то устойчива фаза -φ0, вблизи к-рой ускоряющее поле нарастает со временем.
— нек-рое усреднённое по орбите значение магн. индукции, зависящее от энергии частицы; поэтому характер зависимости Т от ξ оказывается более сложным. Если ∂Т/∂ξ>0, т. е. период растёт с ростом энергии, то, как и раньше, оказывается устойчивой равновесная фаза φ0, вблизи к-рой ускоряющее электрич. поле убывает с увеличением времени. Если же ∂Т/∂ξ<0, т. е. период обращения убывает со временем, то устойчива фаза -φ0, вблизи к-рой ускоряющее поле нарастает со временем.
Для более точного описания изменения фазы следует количественно рассмотреть динамику частицы, энергия к-рой мало отличается от энергии равновесной частицы, движущейся в точном синхронизме с ускоряющим полем и набирающей за каждый оборот энергию eV0cosφs , где φs — равновесная фаза. Неравновесная частица, проходящая ускоряющий зазор в фазе φ, набирает энергию eV0cosφ. Избыточная энергия (по сравнению с равновесным приростом), приобретённая частицей за оборот, равна:
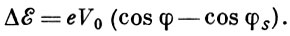 (3)
(3)Этому отклонению энергии соответствует отклонение частоты обращения
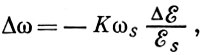 (4)
(4)где ξs и ωs — равновесные значения энергии и частоты в данный момент ускорения, а коэфф. К определяется соотношением
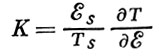 (5)
(5)и является удобной дифференц. характеристикой ускорителя.
Отклонение частоты обращения от равновесной на Δω со приводит к скольжению фазы ускоряющего напряжения со скоростью
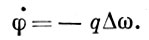 (6)
(6)Соотношения (3), (4) и (6) и определяют колебания фазы и энергии во времени.
Переходя в (3) к изменению энергии в единицу времени (а не за период обращения 2π/ωs), получаем:
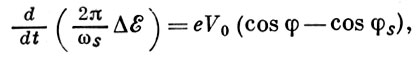
что с учётом (4) и (6) приводит к дифференц. ур-нию для фазы
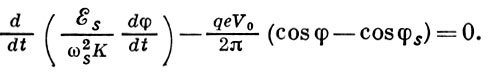
По форме оно совпадает с ур-нием колебаний физ. маятника с моментом инерции I=ξs/ω2sK, моментом силы тяжести Gg=(qeV0/2π)cosφ и внешним момент G=—(qeV0/2π)cosφs (рис. 2). Для маятника физически очевидно, что могут существовать два положения равновесия: φ=φ0 и φ=-φ0. Нижнее положение равновесия (φ=φ0) устойчиво, а верхнее (φ=-φ0) - неустойчиво. Маятник может совершать движения двух качественно разл. типов - либо колебания около устойчивой равновесной фазы φ0 , либо (при очень больших нач. отклонениях от равновесия или при очень больших нач. скоростях) вращат. движение, при к-ром он проходит все углы φ.
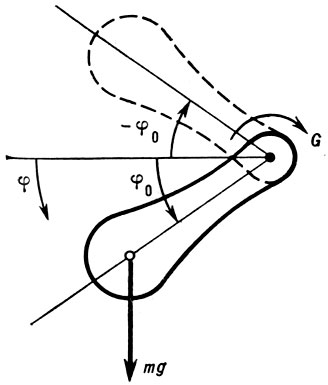
Рис. 2
Соответственно и в ускорителе фаза частицы может либо совершать колебат. движения около равновесной фазы φs (т. н. синхрот ронные колебания), либо скользить по фазе, пробегая все значения фаз. Колебат. движению частицы по фазе соответствуют, согласно (4) и (6), колебания энергии частицы и её частоты обращения вокруг равновесных значений. Существует нек-рая область нач. условий (соответствующая области захвата), при к-рых частица участвует в процессе ускорения, т. е. приобретает в ср. ту же энергию, что и равновесная. Частицы, не попавшие в область захвата, скользя по всем фазам, в ср. энергии не набирают и выпадают из процесса ускорения.
Т. о., если период ускоряющего электрич. поля и величина управляющего магн. поля меняются во времени так, что энергия ξs(t) равновесной частицы, определяемая вытекающим из (2) соотношением
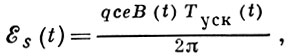
непрерывно растёт, то механизм А. обеспечивает ускорение всего ансамбля частиц внутри области захвата, окружающей устойчивую равновесную фазу.
Приведённые рассуждения справедливы при К>0. Случай К<0 соответствует «отрицат. массе» физ. маятника, так что механич. аналогия становится менее наглядной, но из ур-ния (7) вытекает, что при этом устойчивой оказывается отрицат. фаза -φs, около к-рой существует аналогичная область захвата.
Величина К зависит от параметров структуры ускорителя и от энергии ускоряемой частицы. В нек-рых циклич. ускорителях, напр, в ускорителях с азимутально однородным магн. полем, она сохраняет знак на протяжении всего цикла ускорения. В других — меняет знак при определ. энергии, наз. переходной или критич. энергией. В последнем случае при прохождении критич. значения энергии устойчивая равновесная фаза становится неустойчивой, и наоборот. Для обеспечения дальнейшего ускорения частиц нужно в момент достижения критич. энергии «перенести» все ускоряемые частицы из окрестности прежней равновесной фазы в окрестность новой устойчивой фазы, что технически осуществляется быстрым скачком фазы ускоряющего напряжения.
В линейных ускорителях соотношение (2) заменяется соотношением между временем пролёта Т характерной длины L (расстояния между соседними ускоряющими структурами или длины волны в ускоряющей волноводнои структуре) и скоростью частицы υ:
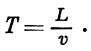
Отсюда видно, что для линейных ускорителей Т всегда уменьшается с ростом энергии, ∂Т/∂ξ<0, так что устойчива всегда отрицат. фаза -φ0 (см. Протонный линейный ускоритель).
В линейных ускорителях требование фазовой устойчивости, или фазировки (φs<0), приходит в противоречие с условием устойчивости движения в поперечном к орбите направлении, т. е. с условием фокусировки частиц в ускорителе, требующим φ>0. В связи с этим был разработан метод знакопеременной фазировки, при к-ром ускоряющие промежутки располагаются так, чтобы в них попеременно происходила то фазировка (а следовательно, расфокусировка), то расфазировка (и следовательно, фокусировка). При надлежащем выборе параметров структуры оказывается возможным одноврем. обеспечение одним и тем же электрич. полем устойчивости движения как в продольном, так и в поперечном направлениях.
А. отсутствует в ускорителях в тех случаях, когда Т не зависит от ξ. В циклич. ускорителях это имеет место в изохронном циклотроне, а в линейных - при релятивистских скоростях ускоряемых частиц, когда скорость практически не меняется с увеличением энергии.
Лит.: Коломенский А. А., Лебедев А. Н., Теория циклических ускорителей, М., 1962; Вальднер О. А., Власов А. Д., Шальнов А. В., Линейные ускорители, М., 1969; Лебедев А. Н., Шальнов А. В., Основы физики и техники ускорителей, ч. 1, М., 1981.
Источники:
- Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.
|
ПОИСК:
|