АДИАБАТИЧЕСКИЕ ИНВАРИАНТЫ

Расстановка ударений: АДИАБАТИ`ЧЕСКИЕ ИНВАРИА`НТЫ

АДИАБАТИЧЕСКИЕ ИНВАРИАНТЫ — физ. величины, остающиеся практически неизменными при медленном (адиабатическом), но не обязательно малом изменении внеш. условий, в к-рых находится система, либо самих характеристик системы (внутр. состояние масса, электрический заряд и пр.). Отмеченное изменение должно происходить за времена (τ), значительш превышающие характерные периоды движения системы (Т).

В классич. механике А. и. являются переменны действия

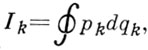
где p_K — обобщённый импульс, q_K — обобщённая координата, интегрирование производится по периоду (или квазипериоду).

Для гармонич. осциллятора А. и. является отношение его энергии к частоте. Характерно, что адиабатич. изменении условий становятся связанным между собой физ. величины, к-рые вообще независимы напр, амплитуда колебаний маятника и его длина.

Физически важным примером А. и. служит магн. момент, создаваемый током заряж. частицы при её движении в медленно меняющемся (в пространств или во времени) магн. поле:

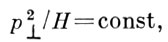
где р_⊥,— проекция импульса заряж. частицы на плоскость, перпендикулярную направлению магн. поля (Н) в данной точке пространства.

На сохранении А. и. основано т. н. дрейфовое принижение, широко используемое в физике плазмы, а также действие «магн. пробок» и основанных на них адибатич. ловушек — пробкотронов (см. Открытые ловушки), применяемых в исследованиях по удержанию горячей плазмы для целей управляемого термоядерного синтеза и осуществляющихся, напр., в магн. поле Земли (см. Радиационный пояс).

Кол-во А. и. не превышает числа степеней свободы, по к-рым движение системы финитно (ограничено в пространстве). Так, в магн. ловушках, кроме магн. момента, может сохраняться продольный А. и., соответствующий движению вдоль магн. силовых линий:

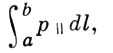
где р_|| — проекция импульса частицы на направление Н, а интеграл берётся вдоль траектории между точками поворота частицы.

Расчёты, проводимые в небесной механике, а также исследования длительности удержания заряж. частиц в адиабатич. ловушках вызвали вопрос о точности, с к-рой сохраняются А. и. Строго говоря, А. и. может изменяться в значит, пределах, если во временной зависимости внеш. условий присутствуют частоты, кратные частотам самой системы (параметрический резонанс). Если не рассматривать такие ситуации, то А. и. сохраняется с точностью большей, чем любая степень малого параметра ^Т/_τ.

Интерес к А. и. сильно возрос в годы установления понятий квантовой механики. В квантовой механике А. и. являются те из квантовых чисел (n), для к-рых частоты ω=^{(ε_n+1-ε_n)}/_ћ (где ε — энергия) удовлетворяют условию адиабатичности (ωτ >> 1). Иными словами, квантовая система, находящаяся под адиабатич. воздействием, остаётся в одном и том же состоянии (хотя само состояние меняется, адиабатически следуя за изменением внеш. воздействия). Все переходы такой системы из одного состояния в другое наз. неадиабатическими переходами и связаны с пересечением соответствующих уровней энергии (ω=0) (см. Пересечение уровней).

Лит.: Шифф Л., Квантовая механика, пер. с англ., 2 изд., М., 1959; Ландау Л. Д., Лифшиц В. М., Теоретическая физика, т. 1— Механика, 3 изд., М., 1973; Нортроп Т., Адиабатическая теория движения заряженных частиц, пер. с англ., М., 1967; Арнольд В. И., Математические методы классической механики, 2 изд., М., 1979.

А. М. Дыхне

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.