АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ

Расстановка ударений: АДИАБАТИ`ЧЕСКОЕ ПРИБЛИЖЕ`НИЕ

АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ — метод приближённого решения задач квантовой механики, применяемый для описания квантовых систем, в к-рых можно выделить «быструю» и «медленную» подсистемы. Исходная задача решается в два этапа: сначала рассматривается движение быстрой подсистемы при фиксир. координатах медленной подсистемы, а затем учитывается движение последней.

Если r и R — соответственно координаты быстрой и медленной подсистем, то полный гамильтониан системы можно представить в виде

,

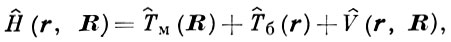где _б(r) и _M(R) — операторы кинетич. энергии быстрой и медленной подсистем, a 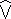(r, R) — оператор потенциальной энергии всей системы. В А. п. из решения ур-ния

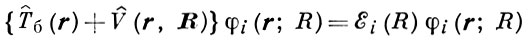
сначала находят волновые ф-ции φ_i(r;R) быстрой подсистемы при фиксир. значениях координат R и собств значения энергии ε_i(R) быстрой подсистемы (термы спектральные), к-рые зависят от координат R медленной подсистемы так, как от параметра.

Полная волновая ф-ция системы представляется в виде разложения по базису φ_i(r; R):

,

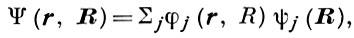где под знаком суммы следует понимать не только суммирование по дискретному спектру, но также интегрирование по сплошному спектру j оператора

.

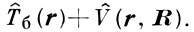При подстановке этого разложения в ур-ние Шрёдингера

,

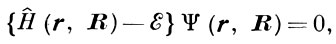где ε — энергия всей системы, домножении его слева на ф-ции φ_i(r; R) и интегрировании по переменным r возникает бесконечная система ур-ний

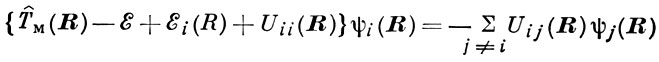
для ф-ций φ_j(R) , описывающих движение медленной подсистемы в эфф. потенциалах ε_i(R) и

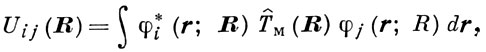
создаваемых движением быстрой подсистемы.

Эта система ур-ний полностью эквивалентна исходному ур-нию Шрёдингера с гамильтонианом (r, R). Она может быть использована для прецизионных расчётов свойств квантовых систем, точность к-рых сравнима с точностью наилучших расчётов, проведённых вариационными методами. Такое описание квантовых систем получило в англоязычной литературе назв. метода возмущённых стационарных состояний; в совр. литературе используют также термин «адиабатич. представление», наиб, адекватно отражающий суть и особенности обсуждаемого подхода.

Собственно А. п. в его первонач. формулировке, известное в литературе как Борна-Оппенгеймера метод, состоит в предположении, что U_ij(R)=0. В этом случае волновую ф-цию системы можно приближённо представить в виде произведения:

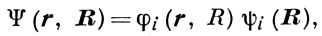
т. е. движения быстрой и медленной подсистем в данном приближении независимы. Для уточнения такого приближённого решения необходимо учесть неадиабатич. матричные элементы U_ij(R), осуществляющие связь между движениями медленной и быстрой подсистем.

«Классич. область» приложения А. п. в квантовой механике — теория молекулярных спектров, а методически наиболее простой случай его использования — молекулярный ион водорода H₂⁺. В теории спектров молекул оператор _б(r) соответствует движению электронов, а оператор T_м(R) — относит, движению ядер в молекуле. Следуя Борну и Оппенгеймеру, можно ввести параметр неадиабатичности χ=(m/М)^1/4, где m — масса электрона, а М — приведённая масса ядер молекулы. Физ. смысл параметра χ — отношение среднеквадратичного отклонения ядер от положения равновесия к размеру молекулы, к-рый определяется протяжённостью электронного облака. Используя параметр χ, полную энергию S системы можно приближённо представить в виде

,

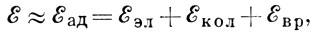где ε_эл≈ε_i(R₀) — энергия электронов в молекуле, приближённо равная значению терма ε_i(R) при равновесном расстоянии R₀ между ядрами, ε_кол≈ χ²ε_эл — энергия колебаний ядер вблизи положения равновесия R₀, ε_вр≈ χ⁴ε_эл — вращат. энергия молекулы.

Указанный результат для ε_ад следует из ур-ний адиабатич. подхода при отбрасывании матричных элементов U_ij (R) при i≠j. Недиагональные матричные элементы U_ij(R) имеют порядок малости 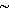χ⁴=^m/_М и описывают связь колебаний с вращениями молекулы и другие, более тонкие эффекты. Их учёт приводит к появлению в разложении для S по степеням х членов 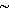χ⁶ и более высоких.

А. п. эффективно используется также в квантовой химии для построения волновых ф-ций многоэлектронных молекул, в атомной физике при описании медленных столкновений атомов и молекул и в теории твёрдых тел.

Лит.: Борн М., Хуан Кунь, Динамическая теория кристаллических решеток, пер. с англ., М., 1958; Давыдов А. С., Квантовая механика, 2 изд., М., 1973; Слэтер Дж., Электронная структура молекул, пер. с англ., М., 1965; Никитин Е. Е., Уманский С. Я., Неадиабатические переходы при медленных атомных столкновениях, М., 1979.

Л. И. Пономарёв

Источники:

1. Физическая энциклопедия/Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т.I. Ааронова - Бома эффект - Длинные линии. 1988. 704 с., ил.