ГЛАВА ШЕСТАЯ

Через несколько лет космонавты возвратятся с Марса. Они привезут с собой тонны кинопленки и образцов. Но не в этом будет главная ценность их полета — все это могут доставить и роботы. Космонавты привезут с собой впечатления. Об этих впечатлениях им будет очень трудно рассказать. Прежде всего потому, что в земном языке нет слов, которые бы точно соответствовали всему тому, что их поразило.

Глава шестая

Но с этой трудностью они сообща справятся уже во время долгого обратного пути: перебирая недавние впечатления, они будут вынуждены придумать для них новые слова или непривычные сочетания слов — иначе они просто не смогут между собой договориться.

Настоящие трудности начнутся потом, по возвращении на Землю, когда они захотят рассказать о своих впечатлениях всем остальным. Ведь все те, кто не летал вместе с ними, будут понимать их слова по-старому, по-земному. Пройдет немалое время, прежде чем слушатели овладеют новыми словами и станут вкладывать в них тот же смысл, что и сами космонавты.

Так происходит всегда: в науке и в искусстве, в технике и политике. Значение слов определяется традицией и привычкой, но их истинный смысл выясняется только в контексте. Узнавая новые явления, человек называет их старыми словами, но вкладывает в них другой смысл — смысл, который нельзя понять, если не знать происхождения новых понятий и их связей с прежними.

Это стремление хоть как-то отделить нужное значение слов от привычного приводит к появлению жаргона в науке, который вызывает понятное недовольство редакторов. Дилетанты от науки впадают в другую крайность: они воспринимают все ее утверждения буквально, не зная той сложной системы условностей, которыми окружено любое утверждение науки. Сплошь и рядом из-за этого возникают недоразумения — смешные для физиков, огорчительные для самих дилетантов.

В конце прошлого — начале нашего века физики открыли новый мир — мир атома. Их ошеломило богатство новых явлений, форм и закономерностей. Они наскоро придумали им названия, но не вполне понимали, какой смысл в них надо вкладывать. В поисках однозначности многие из них вообще перестали доверять словам и верили только уравнениям. То было «смутное время» в физике, хотя именно тогда были добыты основные факты, которыми до сих пор жива наука об атоме. Пока что мы стремились узнать как можно больше таких фактов. Теперь попытаемся найти слова, чтобы правильно об этих фактах рассказать.

Новый мир — мир атома

Рассказ о квантовой механике мы начали с определения: квантовая механика — это наука о строении и свойствах атомных объектов и явлений. Сразу же оказалось, что мы не в состоянии определить понятие «атом». Вполне однозначно мы не можем определить его и сейчас, хотя знаем о нем гораздо больше, чем вначале. В первой части мы подробно проследили, как под влиянием опытов умозрительные образы сменялись более сложной, менее наглядной, но зато и более реальной картиной атома.

В начале века уже никто не верил в атомы — твердые шарики, и от первоначальных представлений Демокрита сохранилась только одна идея: в природе существует предел делимости материи, после которого она переходит в новое качество.

Ученые постепенно доказали, что атом действительно существует, но совсем не похож на атом Демокрита. Узнали, что он состоит из ядра и электронов. Выяснили, что он может испускать лучи. Установили, что это излучение связано с движением электронов в атоме. Необходимо было найти законы этого движения. И тогда изобрели квантовую механику.

Начал создавать ее Нильс Бор: он первый отчетливо понял, что постоянная Планка h не забавная гипотеза, помогающая объяснить спектр абсолютно черного тела, а физическая реальность, которую необходимо учитывать при объяснении всех атомных явлений. На основе этой идеи он сформулировал свои знаменитые постулаты — о стационарном состоянии и квантовом скачке. Постулаты Бора противоречили всей прежней физике, однако внесли неожиданный порядок в первозданный хаос новых опытных фактов.

Но наука ничего не принимает на веру — даже если это постулаты Бора. Надо было либо отбросить их, либо устранить их противоречия. Как удалось решить эту задачу и построить последовательную теорию атомных явлений — об этом и будет рассказано дальше.

ТЕОРИЯ БОРА ГЛАЗАМИ СОВРЕМЕННИКОВ

В 1949 году Альберт Эйнштейн так вспоминал об эпохе создания квантовой механики.

«Все мои попытки приспособить теоретические основы физики к новым результатам потерпели полную неудачу. Это было так, точно из-под ног ушла земля и нигде не видно было твердой почвы, на которой можно было бы строить. Мне всегда казалось чудом, что этой колеблющейся и полной противоречий основы оказалось достаточно, чтобы позволить Бору — человеку с гениальной интуицией и тонким чутьем — найти главнейшие законы спектральных линий и электронных оболочек атомов, включая их значение для химии. Это мне кажется чудом и теперь. Это наивысшая музыкальность в области мысли».

Издали всегда много легче и надежнее оценивать значение открытий. Современникам гораздо труднее: они еще слишком мало знают, чтобы отличить достоинства теории от ее недостатков. Современники Бора, несмотря на все успехи его теории, были глубоко не удовлетворены.

То, что они писали и говорили в то время, для нас непривычно и поучительно.

«Если это правильно, то это означает конец физики как науки» (А.Эйнштейн, 1913).

«Атом существует вечно, мы это, бесспорно, знаем. Но понимаем ли мы это? Нет, не понимаем. Наше непонимание мы прикрываем непонятными же квантовыми условиями. Процесс лучеиспускания — это акт возрождения разрушенного атома. Механизм его нам непонятен. Свое непонимание мы вновь прикрываем непонятным квантовым условием, второй гипотезой Бора... Весь этот метод Бора основан на квантовании — совершенно слепом, мало логическом процессе - мысли, на формальной, если можно так выразиться, интуиции» (Д. С. Рождественский, 1919).

«Теория квантов подобна другим победам в науке: месяцами вы улыбаетесь им, а затем годами плачете» (Г. Крамере, 1920).

«Законы квантования в своей теперешней формулировке носят до некоторой степени теологический характер, для натуралиста совершенно неприемлемый, так что многие ученые по справедливости возмущаются этими Bauern-Regeln (крестьянскими законами)» (П. Эпштейн, 1922).

«Мы неизмеримо далеки от такого описания атомного механизма, которое позволило бы проследить, например, все движения электрона в атоме или понять роль стационарных состояний...

...Теорию квантов можно сравнить с лекарством, излечивающим болезнь, но убивающим больного» (Г. Крамерс, X. Гольст, 1923).

«Физика теперь снова зашла в тупик, во всяком случае для меня она слишком трудна, и я предпочел бы быть комиком в кино или кем-нибудь вроде этого и не слышать ничего о физике!» (В. Паули, 21 мая 1925г.).

Даже у самого Бора тогдашнее положение теории вызывало «чувство грусти и безнадежности».

Это единодушное недовольство трудно понять тем, кто совсем незнаком со структурой и методами нынешней физики. Чтобы осознать причину подобного недовольства, необходимо хотя бы в общих чертах представить себе внутреннюю логику естественных наук. Занятие это непривычное и, пожалуй, непростое, однако для понимания квантовой механики абсолютно необходимое.

В учебнике квантовой механики человека неискушенного прежде всего поражает обилие формул и уравнений. Довольно скоро он убеждается, однако, что это необходимая, но не самая трудная часть науки об атоме. Гораздо сложнее понять, что скрывается за формулами или, как принято говорить в физике, «понять физический смысл формул». Трудности эти не следует преувеличивать, но, поскольку они все-таки реально существуют, помнить о них полезно. Их суть в том, что многие слова, привычные нам с детства, в квантовой механике мы вынуждены использовать в необычном смысле.

Теория Бора глазами современиков

ЯВЛЕНИЕ, ОБРАЗ, ПОНЯТИЕ, ФОРМУЛА

Всякое познание природы начинается с ощущений: ребенок трогает рукой деревянную лошадь, слушает голос матери, сосет соску — словом, с первых же дней жизни он попадает в мир явлений, которые рождают у него свои образы. Для этих явлений и образов у него нет пока даже названий — лишь постепенно он начинает узнавать слова, им соответствующие, и обучается понимать, какие образы скрываются за словами других людей. Довольно скоро он догадывается, что одни и те же слова рождают у разных людей различные образы, и, наконец, выясняет, что есть слова (или группы слов), которые не связаны непосредственно с образами, хотя и появились благодаря им. Это понятия.

Понятия обобщают коллективный опыт, они намеренно лишены деталей, присущих конкретным образам, и потому пригодны для общения разных людей между собой.

Развиваясь, ребенок начинает мыслить понятиями, он вдруг понимает, что «деревянная лошадь» — только одна из «игрушек», а «вода» — это не обязательно морская вода, вода из реки или из-под крана,— это просто вода. Способность к абстракции — первый признак взрослого человека и непременное условие всякой науки. Иначе она превратилась бы в беспорядочный набор фактов.

Однако и понятия не вполне однозначны — хотя бы потому, что рождают у разных людей различные образы. Даже в повседневной жизни подобное может привести к недоразумениям. В науке это еще опаснее: ведь ее результаты претендуют на объективный смысл и не должны зависеть от капризов воображения или мнений отдельных людей. Поэтому в науке каждому понятию сопоставлен набор символов и чисел и заданы строго определенные правила действий над ними. Этим достигается та однозначность науки, которая позволяет общаться между собой ученым разных стран и поколений.

Связь:

явление -> образ -> понятие -> формула —

можно изобразить схематически и пояснить на примере возникновения понятия волна.

Понятие волна

Люди наблюдали различные явления: волны на море и круги от брошенного камня в пруду, распространение света и колебания струны. У них при этом возникали вполне конкретные образы. Постепенно им стало ясно, что этим разным явлениям присуще нечто общее: все они связаны с некоторым периодическим процессом, характерные признаки которого — явления интерференции и дифракции (о них мы подробно говорили раньше). Так возникло новое понятие волна; А чтобы сделать его вполне однозначным, с ним связали четыре характеристики: амплитуду А, скорость распространения v, длину волны λ и частоту ν.

Точно так же понятие частица не предполагает, что у вас при этом возникает конкретный образ бильярдного шара, дроби или пылинки. Физику вполне достаточно знать, что частица — это некий объект, внутренним строением которого он не интересуется, но у которого есть масса m, скорость v, импульс р = mv и траектория движения, которую физик может проследить.

Траектория — еще одно новое понятие, которое необходимо использовать, определяя понятие «движение частицы». На первый взгляд процесс этот беспределен: чтобы определить понятие, нужно использовать другое понятие, которое вновь необходимо определять, и т. д. Однако это не так. В физике существует несколько первичных понятий, которые можно определить без ссылок на другие, а именно — задав точные рецепты измерения величин, которые этим понятиям соответствуют. Таковы понятия: время t, координата x, заряд е и т. д.

Траектория движения частицы задана, если в каждый момент времени t мы можем указать положение частицы — ее координаты х — в пространстве. Нужно только либо измерить координаты х в моменты времени t, либо вычислить их. Первую задачу решает экспериментальная физика, вторую — теоретическая. Однако вторую задачу можно решить лишь в том случае, если известны физические законы, по которым частица движется.

Что есть физический закон? Это постоянная связь явлений и величин, записанная с помощью математических символов в виде уравнений. Для каждой группы явлений существуют свои законы движения: в механике — одни законы (уравнения Ньютона), в электродинамике — другие (уравнения Максвелла). А все вместе взятое в совокупности: понятия, физические законы, формулы, их выражающие, и следствия из них — принято называть точной наукой.

Каждая законченная наука должна быть логически непротиворечива. Это означает, в частности, что каждое понятие в рамках этой науки можно употреблять только в одном строго определенном смысле. Добиться этого трудно, но необходимо, поскольку ученые, как и все люди, общаются между собой не формулами, а с помощью слов. Формулы нужны им лишь для однозначной записи результатов исследований.

Логическая непротиворечивость

Примером логически завершенной науки долгое время служила механика, которую за ее совершенство назвали классической. Механика — это наука о движении тел. Ее законам подчиняются почти все видимые движения в природе — будь то порхание мотылька или полет планет. Классическое совершенство механики долгое время гипнотизировало ученых, и они пытались объяснить с ее помощью не только механические, но и все другие движения в природе.

«Все единодушно признают, что задачей физики является подведение всех явлений природы под простые законы механики»,— писал Генрих Герц даже в 1894 году, на пороге революции в физике.

Движение — одно из самых сложных понятий физики. С ним воображению вольно связывать любые образы—от шелеста листьев до бегущего носорога. Однако даже самые фантастические картины движения, доступные нашему воображению, содержат нечто общее: перемещение одних объектов относительно других с течением времени. После введения понятия траектории понятие движения становится более определенным — вероятно, потому, что при этом оно вновь приобретает черты наглядности. Только теперь эта наглядность особого сорта: возникающий образ никак не похож на мотылька или носорога. И все же наглядность, связанная с понятием траектории, опасна. Действительно, частое повторение словосочетания «траектория движения» приводит к тому, что оба понятия просто перестают различать, хотя совпадают они только для одного вида движений — механических. Но поскольку условия развития и воспитания человека таковы, что ему трудно вообразить иное движение, кроме механического, то и все другие виды движения он пытается осмыслить также с помощью понятия траектории. Это ему, естественно, не удается, например, при попытке осмыслить электрические движения. Можно, конечно, представить себе высоковольтную линию передачи или междугородный телефон и вообразить, что провода и есть «траектории» электрических сигналов, однако реального смысла такие образы не имеют: волны электрических сигналов не жидкость, текущая по проводам.

Определить понятие движения в квантовой механике еще сложнее. Более того: именно тот день, когда это понятие удалось определить непротиворечиво, можно считать днем рождения современной квантовой механики.

АТОМНАЯ МЕХАНИКА ГЕЙЗЕНБЕРГА

Когда прошел восторг первых успехов теории Бора, i все вдруг трезво осознали простую истину: схема Бора противоречива. От такого факта некуда было укрыться, и им объясняется тогдашний пессимизм Эйнштейна, равно как и отчаяние Паули.

Физики вновь и вновь убеждались, что электрон при движении в атоме не подчиняется законам электродинамики: он не падает на ядро и даже не излучает, если атом не возбужден. Все это было настолько необычно, что не укладывалось в голове: электрон, который «произошел» от электродинамики, вдруг вышел из-под контроля ее законов. При любой попытке найти логический выход из подобного порочного круга ученые всегда приходили к выводу: атом Бора существовать не может.

Однако природе нет дела до наших логических построений: атомы вопреки всякой логике устойчивы и, насколько мы знаем, существуют вечно. А если законы электродинамики не могут обеспечить устойчивость атома, тем хуже для них, значит, движение электрона в атоме подчиняется каким-то другим законам.

Впоследствии оказалось, что постулаты Бора — это удачная догадка о тогда еще неизвестных, но фундаментальных законах, которые чуть позже назовут законами квантовой механики.

Квантовая механика — это наука о движении электронов в атоме. Она первоначально так и называлась: атомная механика. А Вернер Карл Гейзенберг — первый из тех, кому выпало счастье эту науку создавать.

Весной 1925 года по приглашению Бора Гейзенберг приехал в Копенгаген из Мюнхена, где только что закончил университет под руководством Зоммерфельда. В Дании он сразу же попал в обстановку научных споров, в среду людей, для которых физика стала главным делом жизни. Полгода прошли в работе и бесконечных дискуссиях все о том же: почему электрон — объект электродинамики — не подчиняется ее законам в атоме и в чем причина удивительной силы нелогичных постулатов Бора? Наконец, что означает в этом случае само понятие «движение»?

Наступило лето. В июне заболевший Гейзенберг уехал отдохнуть на остров Гельголанд в Балтийском море. Отдохнуть ему не удалось — там он вдруг понял неожиданную истину: нельзя представлять себе движение электрона в атоме как движение маленького шарика по траектории. Нельзя, потому что электрон не шарик, а нечто более сложное, и проследить движение этого «нечто» столь же просто, как движение бильярдного шара, нельзя. И если эта догадка верна, то, пытаясь проследить траекторию электрона в атоме, мы задаем природе незаконные вопросы вроде тех, которые задавали в древности: «На чем держится Земля?», «Где у нее край?» А немного позднее: «Где у нее верх и низ?»

Гейзенберг утверждал: уравнения, с помощью которых мы хотим описать движение в атоме, не должны содержать никаких величин, кроме тех, которые можно измерить на опыте. А из опытов следовало, что атом устойчив, состоит из ядра и электронов и может испускать лучи, если его вывести из состояния равновесия. Эти лучи имеют строго определенную длину волны и, если верить Бору, возникают при перескоке электрона с одной стационарной орбиты на другую. При этом схема Бора ничего не говорила о том, что происходит с электроном в момент скачка, так сказать «в полете» между двумя стационарными состояниями. А все, и Гейзенберг в том числе, по привычке добивались ответа именно на этот вопрос. Но в какой-то момент ему стало ясно: электрон не бывает «между» стационарными состояниями, такого свойства у него просто нет!

А что есть? Есть нечто, чему он не знал пока даже названия, но был убежден: оно должно зависеть только от того, куда перешел электрон и откуда.

До сих пор, исходя из уравнений электродинамики, все пытались найти гипотетическую траекторию электрона в атоме, которая непрерывно зависит от времени и которую можно задать рядом чисел х₁, х₂, х₃, ..., отмечающих положение электрона в моменты времени t₁, t₂, t₃. Гейзенберг утверждал: такой траектории в атоме нет, а вместо непрерывной кривой X(t) есть набор дискретных чисел X_nk, значения которых зависят от номеров n и k начального и конечного состояний электрона.

Это важное и довольно сложное утверждение можно пояснить простой аналогией. Представьте, что перед вами шахматная доска, по которой ползет муха. При желании можно очень подробно проследить ее путь, если в каждый момент времени t отмечать ее положение х. По этим измерениям вы затем легко сможете начертить кривую X(t), то есть траекторию движения мухи. Если у вас нет такого желания, то вы можете ограничиться только указанием квадратов, которые посетила муха на своем пути. Это тоже даст некую информацию о ее перемещении, но легко сообразить, что с точки зрения классической механики такое описание будет неполным.

Теперь представьте, что вы за той же доской играете в шахматы и решили, например, сделать традиционный ход е2—е4. В этом случае результат вашего хода совершенно не зависит от того, по какому пути вы передвинули пешку. Это и понятно: правила шахматной игры не зависят от законов механики, а потому и не нуждаются в понятии траектории.

Гейзенберг сообразил, что «правила атомной игры» тоже не требуют знания траектории. В соответствии с этим ой представил состояние атома в виде бесконечной шахматной доски, в каждом квадрате которой написаны числа X_nk. Естественно, что значения этих чисел зависят от положения квадрата на «атомной доске», то есть от номера n строки (начальное состояние) и номера столбца k (конечное состояние), на пересечении которых стоит число X_nk.

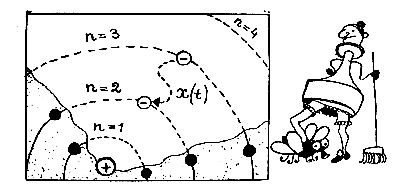
состояние атома в виде бесконечной шахматной доски

Никого не удивляет тот факт, что запись шахматной партии позволяет повторить ее даже много лет спустя. Конечно, при этом мы не узнаем, как долго она длилась в действительности, что переживали при этом шахматисты и как именно двигали они пешки и фигуры. Но это и неважно, коль скоро нам интересна только игра сама по себе.

Точно так же, если нам известны числа X_nk — эта своеобразная запись «атомной игры», — мы знаем об атоме все необходимое, чтобы предсказать его наблюдаемые свойства: спектр атома, интенсивность его спектральных линий, число и скорость электронов, выбитых из атома ультрафиолетовыми лучами, а также многое другое.

Числа X_nk нельзя назвать координатами электрона в атоме. Они заменяют их, или, как стали говорить позже, представляют их. Но что означают эти слова — на первых порах не понимал и сам Гейзенберг.

Действительно, вместо таблицы чисел {Х_nk} с таким же успехом можно нарисовать все, что угодно, скажем цветок, и сказать, что именно он представляет движение электрона в атоме. Однако тут же с помощью Макса Борна (1882—1970) и Паскуаля Иордана удалось понять, что таблица чисел {Х_nk} не просто таблица, а матрица.

Что означает это слово? Математика имеет дело с величинами и символами, и каждый символ в ней подчиняется своим правилам действия. Например, простые числа можно складывать и вычитать, умножать и делить, и результат этих действий не зависит от того, в каком порядке мы эти действия производим: 5 + 3 = 3 + 5 и 5 • 3 = 3 • 5.

Но в математике есть и более сложные объекты: отрицательные и комплексные числа, матрицы и т. д. Матрицы — это таблицы величин типа {X_nk}, для которых существуют свои строго определенные операции сложения и умножения.

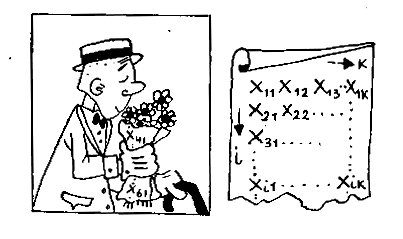
Матрицы

В частности, результат перемножения двух матриц зависит от порядка, в котором они перемножаются, и

{X_nk} • {P_nk} ≠ {P_nk} • {X_nk}.

Это правило может показаться странным и подозрительным, но никакого произвола в себе не содержит. По существу, именно это правило отличает матрицы от других величин. Менять его по своей прихоти мы не вправе — в математике тоже есть свои незыблемые законы. Законы эти, независимые от физики и всех других наук, закрепляют на языке символов все мыслимые логические связи в природе. Причем заранее неизвестно, реализуются ли все эти связи в действительности.

Конечно, математики о матрицах знали задолго до Гейзенберга и умели с ними работать. Однако для всех было полной неожиданностью, что эти странные объекты с непривычными свойствами соответствуют чему-то реальному в мире атомных явлений. Заслуга Гейзенберга и Борна в том и состоит, что они преодолели психологический барьер, нашли соответствие между свойствами матриц и особенностями движения электронов в атоме и тем самым основали новую, атомную, квантовую, матричную механику.

Атомную — потому, что она описывает движение электронов в атоме.

Квантовую — ибо главную роль в этом описании играет понятие кванта действия h.

Матричную — поскольку математический аппарат, необходимый для этого, — матрицы.

В новой механике каждой характеристике электрона: координате х, импульсу р, энергии Е — сопоставлялись соответствующие матрицы: {X_nk}, {P_nk} и {E_nk} — и уже для них (а не для чисел) записывали уравнения движения, известные из классической механики. А затем надо было только проследить, чтобы все действия над величинами {X_nk}, {P_nk}, {E_nk} не нарушали правил математики.

Гейзенберг установил даже нечто большее: он выяснил, что квантовомеханические матрицы координаты {X_nk} и импульса {P_nk} — это не вообще матрицы, а только те из них, которые подчиняются коммутационному (или перестановочному) соотношению:

{X_nk} • {P_nk} - {P_nk} • {X_nk} = i ħ,

где i = √ (-1), а = h/2π.

В новой механике это перестановочное соотношение играло точно такую же роль, как условие квантования Бора в старой механике. И точно так же, как условия Бора выделяли стационарные орбиты из набора всех возможных, коммутационное соотношение Гейзенберга выбирает из множества всех матриц только квантовомеханические.

Не случайно, что в обоих случаях — и в условиях квантования Бора, и в уравнениях Гейзенберга — необходимо присутствует постоянная Планка h. Как мы увидим в дальнейшем, постоянная Планка непременно входит во все уравнения квантовой механики, и по этому признаку их можно безошибочно отличить от всех других уравнений.

Новые уравнения, которые нашел Гейзенберг, были непохожи ни на уравнения механики, ни на уравнения электродинамики и потому никак не могли их нарушить. С точки зрения этих уравнений состояние атома полностью задано, если известны все числа X_nk или P_nk, то есть известны матрицы {X_nk} или {Р_nk}. Причем структура этих матриц такова, что в невозбужденном состоянии атом не излучает.

Обратите внимание: в наших рассуждениях нигде не использовано понятие «движение электрона в атоме». Теперь Оно просто не нужно. Согласно Гейзенбергу движение - это не перемещение электрона-шарика по какой-либо траектории вокруг ядра.

Движение — это изменение состояния системы во времени, которое описывается матрицами {X_nk} и {P_nk}.

Вместе с вопросами о характере движения электрона в атоме сам собой отпал и вопрос, об устойчивости атома. С новой точки зрения в невозбужденном атоме электрон покоится, а потому и не должен излучать.

Теория Гейзенберга была внутренне непротиворечива, чего схеме Бора так недоставало. Вместе с тем она приводила к таким же результатам, что и правила квантования Бора. Кроме того, с ее помощью удалось наконец показать, что гипотеза Планка о квантах излучения Е = hν — это простое и естественное следствие новой механики.

Можно и дальше пытаться без формул излагать следствия механики Гейзенберга. Однако это будет так же неестественно, как попытка пересказать словами музыку.

Чтобы постигнуть глубины квантовой механики, необходимо штудировать математику, учиться работать с матрицами — одним словом, надо овладевать ремеслом физика.

В матрицах нет ничего мистического или непостижимого: изучить их значительно проще, чем усвоить, скажем, латынь. Но, пожалуй, не стоит этого делать в автобусе. Этому, как и музыке, надо учиться специально. Иначе неприятный осадок полузнания отравит даже то удовольствие, которое доступно каждому: без формул и вычислений почувствовать красоту образов и законченность понятий любой глубокой науки.

Глубины математики

Появление матричной механики Гейзенберга физики встретили с огромным облегчением: «Механика Гейзенберга снова вернула мне радость жизни и надежду. Хотя она и не дает решения загадки, но я верю, что теперь снова можно продвигаться вперед»,— писал Паули 9 октября 1925 года.

Возвращение радости жизни

Свою веру он вскоре сам же и оправдал. Применив новую механику к атому водорода, он получил те же формулы, что и Нильс Бор на основе своих постулатов. Конечно, при этом возникли новые трудности, однако это уже были трудности роста, а не безнадежность тупика.

ВОКРУГ КВАНТА

ФУНДАМЕНТ ФИЗИКИ

Основные понятия физики: длина, время, масса, заряд и т. д. — нельзя определить однозначно с помощью слов по двум причинам: во-первых, эти понятия первичны и ни к чему другому более простому не сводятся; во-вторых, физика — наука количественная и потому понятиям сразу же необходимо соотнести числа. Существует только один способ сделать такие понятия однозначными: задать точный рецепт измерения величин, которые им соответствуют.

Мы уже определяли понятие «длина»: 1 м — это такая длина, на которой укладывается 1 650 763,73 волны оранжевой линии спектра Кr-86 в вакууме (изотоп криптона с массовым числом 86). Принятая за эталон, спектральная линия соответствует переходу электрона в атоме криптона между его уровнями 5d и 2р. Один метр приближенно равен 1/40000000 части парижского меридиана, принятой первоначально, в 1799 году, за эталон длины.

Единица массы в 1 кг определяется как масса платино-иридиевого цилиндра специальной формы (его высота 39 мм равна диаметру основания), который изготовлен в 1789 году. Эта масса приближенно совпадает с массой одного литра дистиллированной воды при 4 градусах Цельсия.

Чтобы определить единицу времени, надо использовать какой-нибудь стабильный циклический процесс, например вращение Земли вокруг Солнца. 1 секунда — это 1/31 556 925, 9747 часть тропического года, который равен промежутку времени между двумя одинаковыми положениями Земли относительно звезд. Однако продолжительность тропического года медленно меняется (на 0,5 сек. в столетие) из-за прецессии земной оси и других возмущений, поэтому в эталоне принята продолжительность 1900 года, а точнее — года, который начался в 12 часов дня 31 декабря 1899 года.

С течением времени убедились, однако, что единицу времени — так же, как и единицу длины — лучше всего определять на основе спектроскопических измерений, поскольку до сих пор это самая точная область физики. В 1967 году XIII Генеральная конференция по мерам и весам дала новое определение секунды, согласно которому 1 сек. — это продолжительность 9 192 631 770 периодов излучения, соответствующего переходу электрона между двумя сверхтонкими уровнями основного состояния изотопа цезия с массовым числом 133 (Cs-133).

Переход к атомным стандартам длины и времени был неизбежен не только потому, что спектроскопия — самый точный отдел физики. Дело в том, что атомные стандарты необычайно стабильны: они не зависят ни от температуры, ни от давления, ни даже от космических катастроф, чего нельзя сказать о первоначально принятых эталонах. (Например, «стандартный метр» хранят под стеклянным колпаком, при постоянной температуре и с прочими предосторожностями.) Еще хуже обстоят дела с секундой. В самом деле, если через солнечную систему неожиданно пролетит какое-то небесное тело, то период обращения Земли вокруг Солнца необратимо изменится, а вместе с ним изменится и продолжительность секунды. Ничто подобное не грозит атомным стандартам: они устойчивы и неизменны, как сам атом, на свойствах которого они основаны.

Три величины — метр (м), килограмм (кг), секунда (сек.) — образуют часть системы единиц СИ и достаточны для описания всех механических движений. Электромагнитная теория требует измерения еще двух фундаментальных величин: заряда е и скорости света с. А чтобы описать атомные явления, необходимо знать также величину постоянной Планка h.

Для точного определения фундаментальных физических констант в 1875 году создано Международное бюро мер и весов, которое раз в шесть лет собирает генеральные конференции мер и весов. На этих съездах тщательно оговариваются все подробности условий, в которых происходят измерения: температура, давление, высота над уровнем моря и т. д. Столь же скрупулезно перечисляются все детали приборов для измерения эталонных величин.

Отметим важную особенность таких измерений: только в редких случаях удается определить одну величину независимо от других. Для измерения остальных величин необходимо использовать законы физики. Скажем, если скорость v частицы постоянна, можно определить ее, измерив расстояние Δх, которое частица пройдет за время Δt:

v = (Δх)/(Δt).

Это простой пример того, что все фундаментальные константы в некотором смысле взаимосвязаны. Существует целый специальный и довольно сложный раздел физики, задача которого непротиворечиво определить весь набор этих констант, учитывая одновременно все данные об их измерениях.

Но самый трудный вопрос — это вопрос о границах применимости понятий, определенных таким способом.

Легко сообразить, что единицы измерения — метр, килограмм, секунда — выбраны так, что человеку легко их представить, поскольку они соизмеримы с размерами самого человека. Действительно, 1 м — это рост пятилетнего ребенка, 1 кг весит буханка хлеба, 1 сек. — это один удар сердца. Сохраняют ли эти понятия свой прежний смысл при переходе к очень большим и очень малым расстояниям, массам и промежуткам времени?

Общего ответа на этот вопрос пока не существует. Однако у нас был случай убедиться, что к электрону понятие размера уже неприменимо. В теории атома (где понятие «движение» пришлось заменить новым) прежние понятия «длина», «масса», «время» все еще сохраняют свою силу. Это означает, что, по крайней мере, расстояния 10^-10 м, массы 10^-27 кг и промежутки времени 10^-17 сек. все еще можно понимать в их обычном смысле.

Аналогичная проблема возникает и в астрономии при попытке осмыслить огромные расстояния до галактик и их массы. Пожалуй, здесь она даже труднее, чем в теории элементарных частиц. Действительно, никто не может с легким сердцем утверждать, что он вполне понимает слова «один миллиард световых лет». Формально все предельно просто: это расстояние, которое проходит луч света за 10⁹ лет, то есть расстояние в 10⁹ • 3,15 • 10⁷ сек • 3 • 10⁸ м/сек = 10²⁵ м. Но как понять или хотя бы почувствовать, что в действительности скрывается за этим символом? Для сравнения напомним, что расстояние от Земли до Солнца 1,5 • 10¹¹ м луч света проходит «всего» за 8 минут; до ближайшей звезды — α Центавра — за 4,35 года, а до центра нашей Галактики — за 30 000 лет.

ИСТОРИЯ ПЕРВОГО МЕТРА

В 1788 и 1789 годах многие города Франции обратились к правительству с просьбой о введении единой системы мер, чтобы покончить со злоупотреблениями на этой основе. Талейран (в то время еще епископ Отенский) внес этот вопрос в Национальное собрание. Была создана комиссия французской академии в составе Борда, Лагранжа, Лапласа, Монжа и Кондорсе. Она рекомендовала принять за единицу длины какую-либо часть земного экватора или меридиана, как это давно предлагал инженер-географ Бонн. 30 марта 1791 года Национальное собрание постановило принять в качестве метра одну сорокамиллионную долю земного меридиана. Вскоре после этого Мешен в Испании и Деламбр во Франции приступили к измерению дуги меридиана между Дюнкерком и Барселоной. Время было тревожное — шла Великая французская революция, лишь недавно казнили короля. В землях санкюлотов, где пришлось работать Деламбру, многие колокольни были разрушены, приходилось строить пирамиды из досок и обтягивать их белой холстиной. Но тут взбунтовались окрестные крестьяне: белый цвет — символ королевской власти. Пришлось обшивать полотно по краям голубыми и красными полосами.

В набожной Испании, где работал Мешен, колоколен было сколько угодно, но туда просто не пускали, обвиняя ученых в кощунстве. К тому же все вокруг были напуганы чумой и потому запрещали Мешену свободно переезжать с места на место, заставляли все. его бумаги смачивать уксусом и создавали массу других мелких помех. Разбитый и больной, Мешен хотел просить отставки, но, не дождавшись ее, умер.

Его работу продолжили члены Парижской академии Араго и Био, которым повезло больше: им помогало правительство, протекции крупных епископов и даже один знаменитый главарь разбойников. По окончании работ Био уехал во Францию как раз незадолго до вторжения французских войск в Испанию. Араго тотчас схватили: конечно же, это он расставлял знаки на вершинах, чтобы потом привести по ним французскую армию. В плену Араго читал испанские журналы, в которых сообщалось, что он казнен и принял смерть мужественно, как подобает христианину.

Вскоре, однако, Араго бежит в Алжир и там садится на корабль, идущий в Марсель. Но по дороге корабль захватывают испанские корсары, и снова Араго гоняют по испанским тюрьмам вместе со всяким сбродом. На его счастье, некий африканский властитель на том же корабле посылал подарок Наполеону — двух африканских тигров. Властитель пригрозил войной Испании, корабль был выдан, пленники отпущены и на том же корабле отправились в Марсель. Но корабль сбился с пути и попал в Бужи. Отсюда Араго вернулся опять в Алжир, со многими приключениями прошел пешком Кабилию, его вновь схватили, опять грозили тюрьмой, но, наконец, разрешили вернуться во Францию. Удивительнее всего, что после всех этих нескончаемых приключений записи, зашитые в белье, и даже инструменты остались целыми и невредимыми.

На основании измерений Мешена и Деламбра искусный механик Ленуар изготовил хорошо известный теперь всем эталон метра, и законом от 25 июня 1800 года новая единица длины была введена во всеобщее употребление. «Из всех хороших предприятий, которые у нас останутся в памяти о Французской революции, это то, за которое мы всего менее заплатили...» — писал позднее Деламбр в своем отчете 1806 года.