ГЛАВА СЕДЬМАЯ

В свои 23 года венгерский офицер Янош Бояи открыл неевклидову геометрию и был счастлив этим до тех пор, пока не узнал, что где-то на границе Азии и Европы Николай Иванович Лобачевский опубликовал ту же геометрию несколькими годами ранее. И тогда его жизнь стала походить на кошмар: повсюду ему чудились шпионы и соглядатаи, он стал резок и подозрителен, обвинял всех, даже своего отца, всю жизнь посвятившего той же проблеме. Наверное, Фаркаш Бояи не был так гениален, но он был человечнее и мудрее сына. Умирая, он говорил ему: «Не отчаивайся: когда приходит весна, все фиалки расцветают сразу».

Глава седьмая

В науке об атоме такая весна наступила в 1925 году. Всего за три года появилась, расцвела и даже дала первые плоды новая наука — квантовая механика. С тех пор в ней изменилось очень немногое: так внезапно среди океана возникает вулканический остров и затем уже не меняется столетиями. Конечно, все это — и остров в океане, и весна — неожиданны лишь для тех, кто не следил за подземными толчками и равнодушно проходил мимо набухших почек. В первой части мы стремились почувствовать именно эти глухие толчки, разглядеть то незаметное движение соков, с которых и началась весна квантовой механики.

По-настоящему она пришла тогда, когда Вернер Гейзенберг, взломав лед предрассудков, под коим были погребены застывшие основы физики, дал новую жизнь понятию о движении и создал новую, матричную механику. Это была первая последовательная теория атома, которая объясняла его устойчивость и которую так долго искали. Но (вполне по законам весны!) всего четыре месяца спустя Эрвин Шредингер создал еще одну механику — волновую, которая столь же хорошо объясняла строение атома, но была совсем не похожа на матричную механику.

Впоследствии мы узнаем, что и матричная, и волновая механики просто разные формы записи единой квантовой механики — науки о строении атомов. Но прежде мы должны понять, в чем суть волновой механики, и усвоить те простые идеи, из которых она выросла.

ЛУИ ДЕ БРОЙЛЬ

Гейзенберг родился в 1901 году. Когда он заканчивал гимназию, его родина Германия воевала со всем миром: с Россией — родиной Менделеева, с Англией — родиной Резерфорда. Она воевала и с Францией, где в 1892 году родился принц Луи Виктор де Бройль — потомок королей и будущий нобелевский лауреат. В то время он не занимался физикой — он воевал — и лишь после войны стал работать в лаборатории своего старшего брата Мориса де Бройля. Брат изучал рентгеновские спектры элементов, и поэтому в его лаборатории хорошо знали работы Бора.

Как и многих в то время, Луи де Бройля занимал все тот же вопрос: «Почему атомы устойчивы? И почему на стационарных орбитах электрон не излучает?»

Первый постулат Бора выделял эти орбиты из набора всех мыслимых орбит квантовым условием, которое связывает радиус орбиты r, скорость v и массу m электрона с целым числом квантов действия h:

m v; r = n(h/2π).

Де Бройль хотел найти разумные основания для этого условия, то есть стремился объяснить его с помощью других, более привычных понятий. (Или, как теперь принято говорить, пытался понять его физический смысл.)

Когда ищут объяснение непонятным фактам, как правило, прибегают к аналогиям. Точно так же поступил и де Бройль в поисках выхода из тупика противоречивых представлений об атоме. Он догадался, что трудности эти сродни тем, которые возникли при попытках понять противоречивые свойства света.

Со светом дело запуталось окончательно в 1923 году, когда Артур Комптон поставил свой знаменитый опыт и доказал, что рассеяние рентгеновых лучей на электронах нисколько не похоже на рассеяние морских волн, зато в точности напоминает столкновение двух бильярдных шаров, один из которых — электрон с массой m, а другой — световой квант с энергией E = hν. После опыта Комптона уже нельзя было сомневаться в том, что в природе реально существуют световые кванты, а их энергия E = hν однозначно связанна с длиной световой волны λ = c/ν , которой эти кванты соответствуют. В 1926 году по предложению Дж. Льюиса их стали называть фотонами.

Ни де Бройль, ни его современники не могли объяснить, что означают слова: «Световые кванты соответствуют световой волне». Однако у них не было оснований подвергать сомнению эксперименты, из которых следовало, что в одних условиях световой луч ведет себя как волна с длиной λ и частотой ν = /cλ, а в других — как поток частиц — фотонов — с энергией E = hνи импульсом р = (hν)/c

Вычисления

Года через три-четыре все поймут, что это явление - лишь частный случай корпускулярно-волнового дуализма в природе, но в то время де Бройлю пришлось находить верную дорогу ощупью.

Корпускулярно-волновой дуализм

ВОЛНЫ МАТЕРИИ

Де Бройль верил в единство природы, верил искренне и глубоко — как все великие ученые до него. Поэтому он не мог допустить, что луч света — нечто особенное и ни на что другое в природе не похожее. Де Бройль предположил: не только луч света, но и все тела в природе должны обладать и волновыми, и корпускулярными свойствами одновременно. Поэтому, кроме световых волн и частиц материи, в природе должны реально существовать и кванты света, и волны материи.

Такое простое и сильное утверждение нелегко высказать: для этого нужны смелость и вера. Еще труднее его понять — на это способен лишь непредвзятый ум, привычный к абстрактному мышлению. И это очень трудно представить — природа, доступная восприятию наших пяти чувств, не создала зримых образов, которые могли бы помочь нам в этих усилиях. В самом деле, при слове «частица» вам может прийти на память все, что угодно, — песчинка, бильярдный шар, летящий камень, но вы никогда не вспомните морские волны или колеблющуюся струну. Для нормального человека это настолько противоречивые образы, что объединить их в один кажется противоестественным.

Всякий рассказ о рождении новой физической теории заведомо неточен даже в устах ее создателя: такой рассказ, как правило, использует понятия, которых в момент создания теории не было. У ныне живущих физиков понятие «волна материи» вызывает в сознании некий сложный образ, который ни с чем привычным в окружающем нас мире сравнить нельзя. Образ этот складывается постепенно, при работе с формулами квантовой механики, при решении атомных задач, и рассказать о нем словами довольно трудно. Понятно, что использовать такой сложный и совершенный образ в 1922 году де Бройль не мог, и потому в его тогдашних рассуждениях мы встречаем некий заменитель: образ волны, которая возникает при колебаниях струны.

Хорошо известно, что при ударе по натянутой струне она начинает звучать, и звук этот зависит от длины струны. Механизм возникновения звука также хорошо известен: колебания струны передаются воздуху, и мы воспринимаем уже колебания воздуха, а не колебания струны, которые их породили. Однако между ними существует строгая связь. Например, если мы слышим ноту ля из первой октавы, то в этот момент струна колеблется с частотой ν=440 герц, то есть 440 колебаний в секунду. А поскольку скорость звука в воздухе равна v = 334 м/сек, то длина этих звуковых волн равна

λ = v/ν = 76 см.

Волны материи

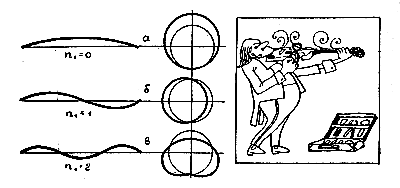
При колебаниях струны мы слышим основной тон — такое колебание, когда вся струна колеблется как целое. Однако при ее возбуждении возникают и дополнительные колебания — обертоны. Картина колебаний усложняется, на струне появляются «узлы», то есть такие точки, которые остаются неподвижными в процессе колебания. Но всегда строго соблюдается одно условие: на длине струны умещается целое число полуволн λ/2 - Для основного тона на длине струны укладывается ровно половина волны λ/2. Для первого обертона — две половины волны, между которыми расположен Неподвижный «узел», и так далее.

Все это де Бройль вспомнил, представив себе колеблющуюся струну. Дальнейшее — сравнительно просто.

Свернем наши струны в кольцо и представим себе, что это орбиты электрона в атоме. Теперь заменим движение электрона по ним колебаниями волн, которые «соответствуют электрону», — де Бройль был убежден, что это разумно. Легко видеть, что при сворачивании струн в кольцо на них появляется дополнительный узел, то есть основной тон растянутой струны превращается в первый обертон кольцевой струны. А это, в свою очередь, означает, что на кольцевой струне может уместиться самое меньшее целая волна λ, а не половина волны λ/2 (как прежде на плоской струне). Таким образом, движение электрона будет устойчивым тогда — и только тогда! — когда на длине орбиты укладывается целое число n «волн электрона» λ. Отсюда следует простое условие:

2 π r= n λ

Де Бройль сравнил это условие с первым постулатом Бора:

m v r = n(h/2π)

и нашел отсюда «длину волны электрона»:

λ = h/(m v)

Волны

Вот и все. Это действительно просто. Но это так же просто, как формула Планка E = hν, как постулаты Бора, как закон всемирного тяготения Ньютона, — это гениально просто. Такие открытия просты, ибо требуют самых простых понятий. Но в истории развития человеческого духа их считанное число, ибо они меняют самые основы нашего мышления. И никогда нельзя до конца понять, как они были совершены. Это всегда чудо, объяснить которое не под силу даже самим создателям. Они могут лишь строго и просто повторить вслед за Ньютоном: «Я все время об этом думал».

Де Бройлю было 30 лет, когда он нашел свою формулу. Но искать ее он начал за одиннадцать лет до этого — с тех самых пор, как его брат Морис приехал из Брюсселя, где был секретарем первого Сольвеевского конгресса. Того самого конгресса 1911 года, на котором Планк рассказал о развитии «гипотезы квант». Значительность открытий, живые впечатления старшего брата от общения с великими физиками настолько поразили воображение младшего, что он не смог забыть их даже на войне. Постоянное напряжение мысли разрешилось наконец в 1922 году гипотезой о волнах материи. Теперь де Бройль смог дать новое определение понятию «стационарная орбита»: это такая орбита, на которой укладывается целое число «волн электрона» λ.

Если это действительно так, то проблемы устойчивости атома не существует, ибо в стационарном состоянии электрон подобен струне, колеблющейся в вакууме без трения. Такие колебания не затухают, а потому без внешнего воздействия электрон останется в стационарном состоянии навсегда.

Самое трудное — высказать гипотезу. Это всегда процесс нелогический. Но как только гипотеза высказана, строгие законы логики позволяют извлечь из нее все следствия. Главное из них очевидно: если «волны материи» существуют, то их можно обнаружить и измерить. Их действительно обнаружили и доказали их реальность с той степенью достоверности, какая вообще доступна в физике. Однако случилось это четыре года спустя; и об этом мы расскажем потом.

Свои формулы де Бройль написал в 1923 году — за два года до работ Гейзенберга и Шредингера. Их простота и прозрачность основной идеи очень напоминали постулаты Бора. И точно так же, как постулаты Бора, идеи де Бройля еще не были теорией атома — для этого их необходимо было записать на языке уравнений. Когда Вернер Гейзенберг создал матричную механику, он тем самым превратил идеи Бора в точные формулы и строгие уравнения.

Идеи де Бройля стали началом волновой механики, которую создал Эрвин Шредингер.

ОПТИКО-МЕХАНИЧЕСКАЯ АНАЛОГИЯ

Сейчас мы должны усвоить несколько новых фактов. Пусть вначале они покажутся не очень простыми — все равно понять их необходимо, если мы не хотим без конца повторять гладкие, обкатанные фразы о «таинственной стране микромира», которые лишь засоряют ум, поскольку на поверку ничего реального не означают.

Говорим ли мы об атомах или о квантах — мы вновь и вновь обращаемся к свойствам светового луча. Это не случайно. По существу, в нем заключена почти вся нынешняя физика. Сейчас мы еще раз — и более пристально — взглянем на его свойства. Для этого нам нужно возвратиться к Исааку Ньютону и вспомнить смысл его спора с Христианом Гюйгенсом о природе светового луча.

Всегда, во все времена все знали, что луч света в пустоте распространяется прямолинейно; это знание человек приобретает в детстве без всякой науки и физических приборов — после того, как несколько раз ушибется об угол стола. Впоследствии это знание помогает ему избегать многих других опасностей, и постепенно он убеждается в его истинности. Чтобы сделать явление распространения луча более наглядным, в учебниках обычно соединяют источник света и глаз наблюдателя прямой линией, то есть рисуют воображаемую траекторию светового луча.

Траектория светового луча

И по смыслу, и по возникающим образам траектория светового луча ничем не отличается от траектории движения частицы. На этом основании во времена Ньютона луч света представляли себе как поток очень маленьких частиц. Конечно, путь этих «световых частиц» (как и путь обычных частиц) может искривляться, допустим, при переходе из воздуха в воду, но понятие траектории ив этом случае сохраняется. В повседневной жизни это понятие очень полезно и не приводит к недоразумениям: оно помогает избегать автомобилей на улицах, определять положение звезд на небе и конструировать фотоаппараты.

Оптико-механическая аналогия

С развитием экспериментальной физики люди раздвинули узкие границы повседневного опыта и обнаружили новые свойства светового луча: оказывается, он нацело теряет свои привычные свойства, если огибает «очень маленькое препятствие». Физика — наука количественная, и в ней такое неопределенное утверждение не имеет смысла. Маленькое — по сравнению с чем?

Христиан Гюйгенс представлял себе распространение света как колебания некоего «светового эфира». Образ, при этом возникающий в сознании, напоминает круги от брошенного в пруд камня либо же бесконечные ряды морских волн. В правомерности этих образов перестали сомневаться вовсе после трудов Максвелла и Герца, которые доказали, что свет — это просто частный случай электромагнитных колебаний.

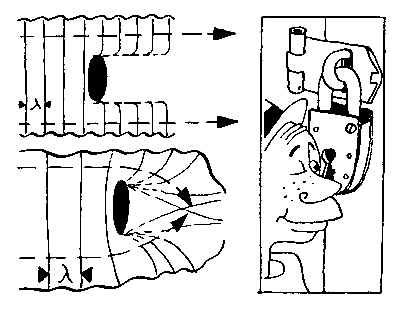
Вспомним (мы об этом говорили в первой главе): у всякого колебания есть характеристика — длина волны. Теперь наше утверждение приобретает строгий смысл: «Луч света теряет свои привычные свойства, если размеры препятствия сравнимы с длиной его волны». В этом случае луч света уже не распространяется прямолинейно — происходит явление дифракции. Кроме того, отдельные волны луча начинают взаимодействовать между собой — усиливать и гасить друг друга, или, как принято говорить в физике, начинают интерферировать. Оба явления — дифракция и интерференция — в конечном итоге дают на экране дифракционную картину, которую с точки зрения Ньютона понять довольно трудно. Волновая же теория света объясняет ее вполне естественно, и это определило ее победу.

Cо временем к свойствам света настолько привыкли, что они превратились в некий эталон для всех вообще волновых процессов. Теперь, если в каком-либо процессе замечали вдруг явления интерференции и дифракции, то уже не сомневались в его волновой природе. Потому, собственно, все сразу и признали гипотезу де Бройля о волнах материи, увидев первые снимки дифракции электронов.

Взгляните на три почти одинаковые фотографии на странице 164: слева — дифракция видимого света, справа — дифракция электронов, внизу — волны на воде. Глядя на них, не поверить в волновую природу электрона очень трудно. Для нынешнего поколения физиков это уже не вопрос веры, а факт точного знания и даже средство для технических приложений.

В стройной теории волновой оптики оставалась одна неувязка: луч света мы воспринимаем все-таки как луч, а не как волну. Как объяснить такой факт с точки зрения волновой оптики? Задачу решил Огюстен Жан Френель, и его объяснение можно найти теперь в любом учебнике физики.

Оказывается, при интерференции все волны от источника света гасят друг друга, кроме тех, которые находятся внутри узкого канала толщиной в половину длины волны света. (Для видимого света толщина канала λ/2 Ǻ 3 10^-5 см.) Если мы пренебрежем толщиной «светового канала», то получим ту самую траекторию светового луча, к которой все мы привыкли в обычной жизни.

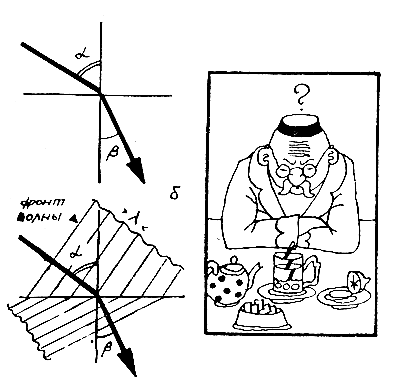
Известен даже способ ее построения: сначала нужно провести линии через все гребни волн — как говорят в физике, отметить фронт волны. А затем от источника света провести линию, которая перпендикулярна к фронту волны. Это и будет траектория светового луча. Если вблизи препятствия фронт волны искажается, то одновременно с этим искривляется и траектория луча — луч света огибает препятствие, происходит, дифракция.

Траектория светового луча

В 1834 году Уильям Роуан Гамильтон (1805—1865), знаменитый профессор астрономии в Дублинском университете, занимался непонятной для современников задачей. Он хотел доказать, что формальная аналогия между траекторией движения частицы и траекторией светового луча имеет строгий математический смысл.

Мы уже знаем: в физике понятию закона движения соответствуют формулы — уравнения движения. Для волн и частиц они совершенно различны: решая одни, мы вычисляем траекторию частицы, решая другие, находим форму и скорость фронта волны. Но мы также знаем, что в оптике можно нарисовать траекторию светового луча, зная движение фронта его волны.

Траектория частицы

Гамильтон доказал, что в механике можно сделать нечто противоположное: заменить траекторию частицы движением фронта некоторой волны. Или более точно: уравнения движения механики можно записать в таком виде, что они полностью совпадут с уравнениями геометрической оптики, которые описывают распространение луча света без учета его волновых свойств. Тем самым Гамильтон доказал оптико-механическую аналогию: движение частицы по траектории можно представить как распространение луча света без учета его волновых свойств.

ВОЛНОВАЯ МЕХАНИКА ШРЕДИНГЕРА

Эрвин Шредингер (1887—1961) в 1911 году окончил Венский университет, где были еще живы традиции Доплера, Физо, Больцмана и весь дух классических времен физики: основательность при изучении явлений и неторопливый к ним интерес. В 1925 году это был уже немолодой профессор Цюрихского университета, сохранивший, однако, юношеское стремление понять самое главное в тогдашней физике: «Как устроен атом? И как в нем движутся электроны?»

В конце 1925 года в одной из статей Эйнштейна Шредингер прочел несколько слов похвалы в адрес де Бройля и его гипотезы. Этих немногих сведений ему оказалось достаточно, чтобы поверить в гипотезу де Бройля о волнах материи и развить ее до логического конца (что всегда трудно, и не только в науке).

Ход его рассуждений легко понять, по крайней мере, теперь, почти полвека спустя. Прежде всего, он вспомнил оптико-механическую аналогию Гамильтона. Он знал, что она доказана лишь в пределе геометрической оптики — тогда, когда можно пренебречь волновыми свойствами света. Шредингер пошел дальше и предположил: оптико-механическая аналогия остается справедливой также и в случае волновой оптики. Это означает, что всегда любое движение частиц подобно явлению распространения волн.

Как и всякое глубокое открытие, гипотеза Шредингера ниоткуда логически не следовала.

Но, как всякое открытие, логические следствия она имела.

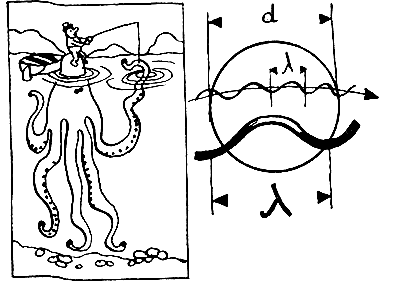
Прежде всего, если Шредингер прав, то движение частиц Должно обнаруживать волновые свойства в тех областях пространства, размеры которых сравнимы с длиной Волны этих частиц. В большой степени это относится и к движению электрона в атоме: сравнив формулы де Бройля (λ = h/mv) и Бора m (λ r = h/2π), легко усмотреть, что диаметр атома d = λ/π примерно в три раза меньше, чем длина волны электрона λ. Но эта длина — единственная, которую мы вспоминаем, когда говорим о размерах электрона в атоме. Теперь становится очевидным, Что представить его в атоме частицей невозможно, ибо тогда придется допустить, что атом построен из таких частиц, которые больше его самого. Отсюда сразу, и немного неожиданно, следует уже известный нам из предыдущей главы постулат Гейзенберга: не существует понятия траектории электрона в атоме.

Действительно, не может нечто большее двигаться внутри чего-то меньшего, и притом еще по какой-то траектории тогда не существует и проблемы устойчивости атома, так как электродинамика запрещает электрону двигаться в атоме лишь по траектории и не отвечает за явления, которые происходят при других типах движений. Все это означает, что в атоме электроны существуют не в виде частиц, а в виде некоторых волн, смысл которых мы поймем немного позже. А пока ясно только одно: какова бы ни была природа этих электронных волн, их движение должно подчиняться волновому уравнению. Шредингер нашел это уравнение. Вот оно:

[(d² ψ)/(d x) + 2m/(ħ²)][Е - U(x)]ψ = 0

Волновая механика

Для тех, кто видит его впервые, оно абсолютно непонятно и может возбудить лишь любопытство или чувство инстинктивного протеста, причем последнее без серьезных оснований.

Волны

В самом деле, представленный на этой странице рисунок столь же непонятен, как и уравнение Шредингера, однако мы принимаем его без внутреннего сопротивления. Мы совсем успокоимся, узнав, что это просто герб города Парижа, в котором мы никогда не были и, быть может, никогда не побываем. Только самые дотошные станут допытываться, почему он выглядит именно так, а не иначе. Как и в уравнении Шредингера, в этом гербе каждая черта и каждый символ исполнены смысла. Вверху — королевские лилии, которые появились в геральдических знаках Франции уже в конце V века — после победы Хлодвига над гуннами у берегов реки Ли. (По преданию, воины Хлодвига, возвращаясь домой, украсили свои шлемы и щиты цветами белых лилий «ли-ли», по-русски «белый-белый»). Внизу герба — корабль, похожий очертаниями на Ситэ — остров посреди Сены, где в древности обитало племя паризиев, по имени которых назван Париж. А форма герба напоминает парус — в память об основном занятии древних обитателей Парижа. Как видите, понять герб несложно, однако только жителям города он по-настоящему близок.

Подойдем к уравнению Шредингера точно так же. Примем его вначале просто как символ квантовой механики, как некий герб квантовой страны, по которой мы теперь путешествуем, и постараемся понять, почему он именно таков. Некоторые штрихи в этом гербе нам уже понятны: m — это масса электрона, ħ — постоянная Планка h, деленная на 2π, Е — полная энергия электрона в атоме, U(x) — его потенциальная энергия, х — расстояние от ядра до электрона. Несколько сложнее понять символ второй производной d²/dx², но с этим пока ничего нельзя поделать, вначале придется просто запомнить, что это символ дифференциального исчисления, из-за которого уравнение Шредингера не простое, а дифференциальное.

Самое сложное — понять, что собой представляет ψ-функция (читается: пси-функция). Это действительно не просто, и вначале даже сам Шредингер истолковал неправильно ее смысл. Мы также поймем его несколько позднее, а сейчас важно усвоить следующее: несмотря на свою необычность, пси-функция все же как-то представляет движение электрона в атоме. По-другому, чем матрицы Гейзенберга {X_nk} и {Р_nk}, но все-таки представляет, и притом хорошо. Настолько хорошо, что с ее помощью многие задачи квантовой механики можно решать значительно проще и быстрее, чем с помощью матриц Гейзенберга.

Физики довольно быстро оценили преимущества волновой механики: ее универсальность, изящество и простоту, и с тех пор почти забросили механику матричную.

Однако победа далась не сразу.

ВОКРУГ КВАНТА

ОПЫТ КОМПТОНА

Представьте себе, что вы стоите перед зеркалом в зеленом свитере и вдруг замечаете, что ваше изображение одето в красный свитер. Прежде всего вы, вероятно, протрете глаза, а если это не поможет, пойдете к врачу. Потому что «так не бывает». В самом деле, зеленые лучи — что волны, длина которых λ = 5500 Ǻ. Встретив на пути препятствие — зеркало, они отражаются, но при этом никак не могут изменить свою длину и стать, например, красными (λ = 7500 Ǻ). А Комптон наблюдал именно это явление. Направив на мишень пучок рентгеновых лучей с длиной волны λ, он обнаружил, что длина волны рассеянных лучей λ^' больше длины волны падающих, то есть рассеянные лучи действительно «краснее» первоначальных!

Чудо это можно понять, если вспомнить гипотезу Эйнштейна о квантах света, которую он предложил для объяснения явлений фотоэффекта. Действительно, в этом случае вместо рентгеновых волн с длиной λ и частотой ν = c/λ нужно представлять себе поток частиц—квантов с энергией E = h ν. Сталкиваясь с электронами атомов мишени, они выбивают их оттуда (затратив энергию Р), разгоняют до скорости v (дополнинительно затратив энергию (mv2))/2, а сами рассеиваются с меньшей энергией E^' = h v^'. Очевидно, что h ν = h ν^' + P + (mv2))/2.

Если атом полностью поглотит квант света (E^' = 0), то мы увидим обычное явление фотоэффекта, а уравнение Комптона превратится в уравнение Эйнштейна:

h ν = P + (m v²)/2

Оба эти опыта можно провести в камере Вильсона, проследить путь каждого выбитого электрона и тем самым наглядно представить процесс столкновения светового кванта с электроном.

Но в таком случае что нам мешает увидеть себя в красном свитере? Оказывается, все те же квантовые законы, которые запрещают электрону поглощать произвольные порции энергии. Электрон на стационарной орбите в атоме может поглотить только такой квант, который либо перебросит его из одного стационарного состояния в другое, либо выбросит его из атома (вспомните опыт Франка и Герца). Энергия «зеленых квантов» (длина их волны (λ = 5,5 • 10^-5 см = 5500Ǻ) равна

E = h ν = ((h c)/λ = 6,62 • 10^-27 • 3 • 10¹⁰)/(5,5 • 10^-5) = 3,6 • 10^-12

эрг ≈ 2эв.

А этого слишком мало, чтобы вырвать электрон из атома (нужно впятеро больше, Р ≈ 10 эв). Поэтому они упруго (без потери энергии) отразятся от атомов зеркала и при этом нисколько не «покраснеют».

Совсем другую картину являют собой рентгеновы лучи (λ ≈ 1 Ǻ). Их энергия примерно в 5—10 тысяч раз больше, и потому явления, которые с ними происходят, иные. Например, они вовсе не отражаются от зеркала, а свободно через него проходят, срывая по пути электроны с его атомов.

Конечно, даже простой процесс отражения зеленого света от зеркала несколько сложнее, чем мы это сейчас представили. Но существует еще одна — главная — трудность: в нашей стройной картине, где вместо волн света сплошь одни только кванты света, нет места опытам Фридриха, Книппинга и Лауэ, которые открыли дифракцию рентгеновых лучей и тем самым доказали их волновую природу.

Как примирить эти несовместимые представления: лучи-волны и лучи-кванты?

В следующей главе мы увидим, что квантовая механика справилась и с этой задачей.

ЭЛЕКТРОН: ЧАСТИЦА ИЛИ ВОЛНА?

Мы не думаем об этом каждый день, точно так же, как и об устройстве телефона. Мы просто пользуемся приборами, в которых электрон «работает», — телевизором, рентгеновским аппаратом, электронным микроскопом. Но если задуматься, как устроены эти аппараты, то вопрос о природе электрона сразу потеряет свой академический характер.

В телевизионной трубке изображение получают с помощью электронов, которые разгоняются напряжением V ≈ 10 000 в. При этом они приобретают скорость v; ≈ 5 • 10⁹ см/сек — всего в шесть раз меньше скорости света. Длину их волны легко вычислить по формуле де Бройля: λ = h/m v, она равна λ ≈ 0,1 Ǻ то есть в 10 раз меньше размеров атома. И поскольку в телевизоре электроны распространяются прямолинейно, мы их воспринимаем как поток частиц.

В электронном микроскопе тот же электрон работает как волна: пучок электронов разгоняют напряжением в 100000 вольт до скорости 10¹⁰ см/сек, что соответствует длине волны в 0,05 Ǻ. Кроме того, этот пучок проходит через систему магнитных линз, точно так же, как в обычном микроскопе луч света проходит через линзы оптические. В волновой оптике хорошо известно, что из-за явлений дифракции даже в лучший микроскоп нельзя разглядеть предмет, если его размеры меньше, чем половина длины волны света, которым он освещен. Длина волны видимого света равна 5000 Ǻ, поэтому в обычный микроскоп можно различать лишь предметы, размеры которых превышают 2500 Ǻ. Размеры бактерий превышают 10^-4 см = 10 000 Ǻ, поэтому их легко наблюдать в обычный микроскоп. Но уже вирусы в такой микроскоп различить нельзя: их размеры меньше 1000 Ǻ (например, диаметр вируса гриппа всего 800 Ǻ).

Теоретически электронный микроскоп позволяет разглядеть объекты размером до 0,02 Ǻ, то есть в 50 раз меньше атома. Означает ли это, что мы можем таким способом рассмотреть отдельный атом? Нет, конечно. Энергия связи электрона в атоме (Р) равна примерно 10 электрон-вольтам (энергия, которую приобретает электрон, пройдя разность потенциалов 10 в). А в электронном микроскопе электроны приобретают энергию около 100 тыс. электрон-вольт. Такие «лучи» сразу же, при первом столкновении с атомом, разрушат его. (В самом деле, легко сообразить, что если мы захотим получить на стене тень от пылинки, стреляя по ней из ружья, то ничего хорошего из такой затеи не выйдет.) Реально в электронный микроскоп удалось пока рассмотреть объекты размером 5—10Ǻ, то есть в 5—10 раз больше атома.

ДИФРАКЦИЯ ЭЛЕКТРОНОВ

Как и многие открытия в физике, дифракция электронов была обнаружена во многом «случайно», хотя, как любил повторять Пастер, «случай говорит только подготовленному уму».

В 1922 году по заказу американской фирмы «Белл-телефон» Клинтон Джозеф Дэвиссон (1881 —1958) и его сотрудник Кенсмен изучали отражение электронных пучков от поверхности металлов и вдруг заметили какие-то аномалии. В 1925 году, после работ де Бройля, ученик Макса Борна Вальтер Эльзассер предположил, что эти аномалии объясняются электронными волнами. Дэвиссон прочел эту заметку, но не придал ей значения. В 1926 году он приехал в Европу и показывал свои графики Максу Борну и Джеймсу Франку в Геттингене, а также Дугласу Хартри в Оксфорде. Все они единодушно признали в них волны де Бройля. В пути через океан Дэвиссон изучал работы Шредингера и вскоре по приезде в Америку вместе с Лестером Альбертом Джермером (род. 1896) подтвердил гипотезу де Бройля опытом.

Дж. П. Томсон подошел к проблеме с другого конца. Он с самого начала относился к гипотезе де Бройля с большим сочувствием и вскоре после посещения Англии Дэвиссоном стал обдумывать способы доказать ее на опыте. В Англии после работ Крукса и Дж. Дж. Томсона опыты с катодными лучами стали непременным и привычным элементом образования. Быть может, поэтому Дж. П. Томсон прежде всего задумался, а нельзя ли приспособить их для новых опытов. Почти сразу же отыскалась подходящая готовая установка в Абердине, с которой работал студент Александр Рейд. Уже через два месяца они получили на этой установке прекрасные фотографии дифракции электронов, которые в точности напоминали дифракцию рентгеновых лучей. Это было естественно, поскольку в их опытах электроны ускорялись потенциалом в 150 в (обычное напряжение городской сети). Длина волны таких электронов равна примерно Ǻ = 10^-8 см, то есть сравнима с длиной волны рентгеновых лучей и с размерами атомов.

Небольшая справка: Джордж Паджет Томсон — сын знаменитого Джи-Джи — Джозефа Джона Томсона, который в конце века установил, что электрон — это частица. По иронии судьбы тридцать лет спустя сын доказал, что электрон — это волна. И оба они правы, оба удостоены Нобелевской премии, за свои открытия.

ЗАГАДОЧНАЯ БУКВА Ψ

Греческую букву ψ («пси») для обозначения волновой функции Шредингер выбрал более или менее случайно. Но для многих она стала неким символом непонятности квантовой механики. Чтобы лишить ее мистического ореола, предлагаем читателям проследить предполагаемую эволюцию буквы «буки» древнерусского письма «глаголицы» и ее связь с более древними знаками и символами.

Качественный электрокардиограф 12-канальныйкупить выгодно.