
ЧЕЛОВЕК - СУЩЕСТВО СИММЕТРИЧНОЕ
Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае у большинства людей. И все же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! Стоп. Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так.
Ну конечно, каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Именно вопросам симметрии и зеркального отражения и посвящена лежащая перед вами книга.
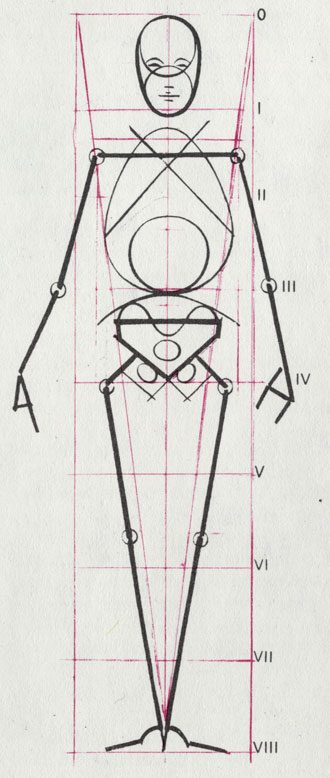
Рост человека в восемь раз больше размера его головы. Общий абрис его тела можно представить в виде простых геометрических фигур
Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае до тех цор, пока ими руководило желание в своих произведениях как можно точнее следовать природе. Известны каноны продорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя).
В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлиненным черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлиненной формы.
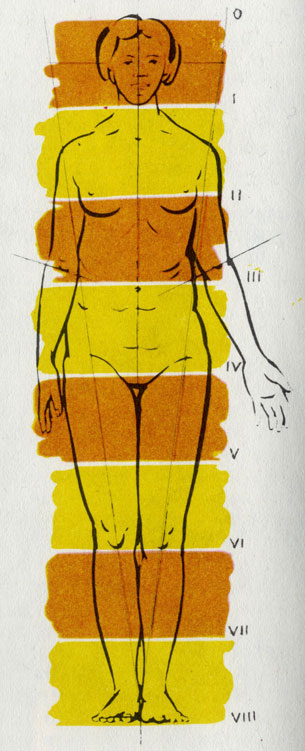
Человеческую фигуру, отвечающую определенным пропорциям, мы воспринимаем как совершенную (но вовсе не обязательно как привлекательную)
Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы в общем похожи друг на друга. (К сходству или подобию мы еще вернемся через несколько страниц.) Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчеркивают эту симметрию.
БЕЗУКОРИЗНЕННАЯ СИММЕТРИЯ СКУЧНА
И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина - левой.
Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Лишь изредка женщина обладает достаточной смелостью, чтобы надеть по-настоящему асимметричное платье (насколько сильные отклонения от симметрии допустимы, мы увидим дальше).
Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор - слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди, нередко подчеркнутый еще и платочком. Или надев кольцо на безымянный палец только одной руки. Лишь на одной стороне груди носятся ордена и значки (чаще на левой).

Время от времени у мужчин входят в моду длинные волосы. Альбрехт Дюрер смягчил в своем автопортрете строгую симметрию маленькими отклонениями от нее
Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от нее и придают характерные, индивидуальные черты. Знаменитый автопортрет Альбрехта Дюрера на первый взгляд кажется абсолютно симметричным. Но, приглядевшись внимательней, вы заметите маленькую асимметричную деталь, которая и сообщает картине живость и жизненность: прядку волос возле пробора.
И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или белой). А в наши дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна. Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.
ЧТО ТАКОЕ ПОДОБИЕ?
Нередко мы говорим, что какие-то два человека похожи друг на друга. Дети обычно похожи на своих родителей (во всяком случае, по мнению их бабушек). Похожи, но не одинаковы!
Попробуем разобраться, что понимается под сходством или подобием в математике. У подобных фигур соответствующие отрезки пропорциональны друг другу. В нашем случае мы можем сформулировать это положение так: подобные носы имеют одинаковую форму, но могут отличаться размером. При этом каждому отдельному участку носа (например, переносице) должны быть пропорциональны все остальные.
Этот закон подобия иногда таит в себе подвох. Например, в задаче такого рода:
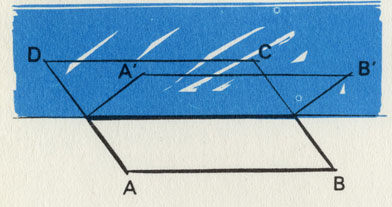
Высота башни А 10 м. На некотором расстоянии X от нее находится шестиметровая башня В. Если провести прямые от подножия и от вершины башни А через вершину башни В, то они встретятся соответственно с подножием и вершиной башни С, имеющей высоту 15м. Каково расстояние от башни А до башни В?
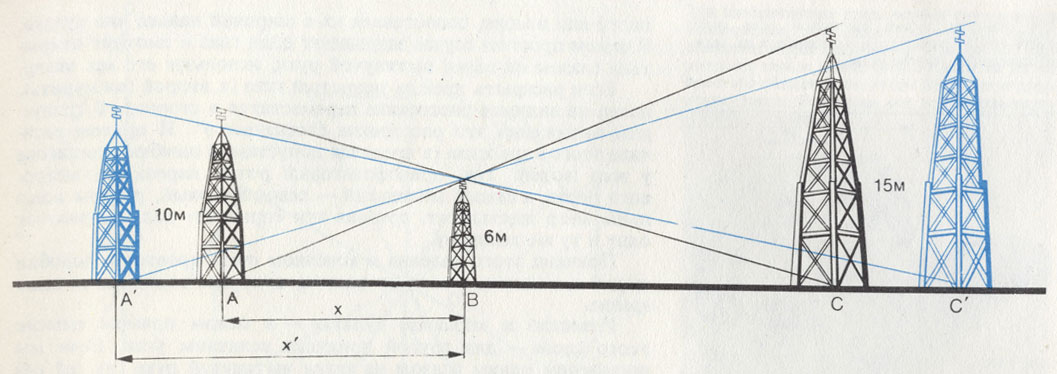
Требуется определить величину отрезка X, исходя из известной высоты трех башен. Как видно из цветного построения, решений здесь существует бесконечное множество. Это типичный пример задачи с 'ловушкой'
Казалось бы, для решения достаточно взять в руки циркуль и линейку. Но тут же выяснится, что ответов будет бесконечное множество. Иными словами, на вопрос о значении X не может быть однозначного ответа.
В этой книге вы нередко будете сталкиваться с задачами, требующими размышлений. В этом есть определенный педагогический смысл. Такого рода задачи, даже если они и не имеют решения, как, например, предложенная выше, касаются какой-либо проблемы, лежащей у пределов нашего знания. Большей частью это те самые пределы, перед которыми пасует знаменитый «здравый смысл», и лишь строго математическое логическое мышление вкупе с естественнонаучным познанием способно привести к правильному решению.
Обратимся снова к человеку: при сравнении живых существ сходство ощущается явно, если совпадают их пропорции. Поэтому могут быть похожи дети и взрослые. Хотя масса и размеры любой из частей тела, будь то нос или рот, различны, но пропорции похожих индивидов совпадают.
Поразительный пример подобия - глазомерная оценка расстояния с помощью большого пальца. Таким способом военные и моряки прикидывают расстояние между двумя пунктами на местности или в море, сопоставляя их с шириной пальца или кулака. В самом простом случае закрывают один глаз и смотрят открытым глазом на палец вытянутой руки, используя его как визир.
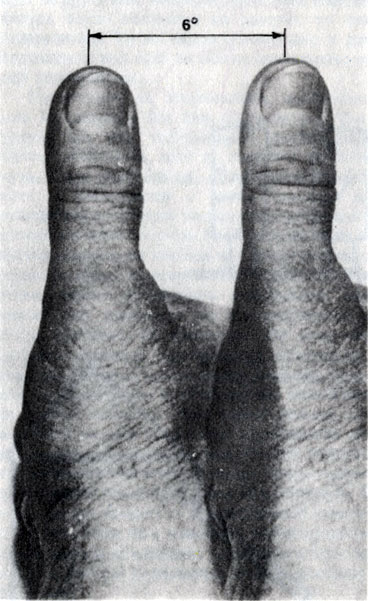
При визировании с помощью большого пальца вытянутой руки (один раз левым глазом, а другой - правым) палец 'отскакивает' примерно на 6°
Если раскрыть прежде закрытый глаз (а второй зажмурить), палец на видимое расстояние переместится в сторону. В градусном выражении это расстояние составляет 6°. И притом величина этого «прыжка» (в пределах допустимой ошибки) одинакова у всех людей! Так, правофланговый роты, парень двухметрового роста, и самый маленький - левофланговый, ростом всего лишь метр шестьдесят, сравнив эти «прыжки» пальца, получат одну и ту же величину.
Причина этого явления в конечном счете кроется в подобии людей и, конечно, в законах оптики, которым подчиняется наше зрение.
Известно и «правило кулака» - в самом прямом смысле этого слова - для грубой прикидки величины угла. Если мы посмотрим одним глазом на кулак вытянутой руки (на сей раз одним и тем же глазом), то ширина кулака составит 10°, а расстояние между двумя косточками фаланг 3°. Кулак и оттопыренный в сторону большой палец составят 15°. Комбинируя эти мерки, можно приблизительно измерить все углы на местности.
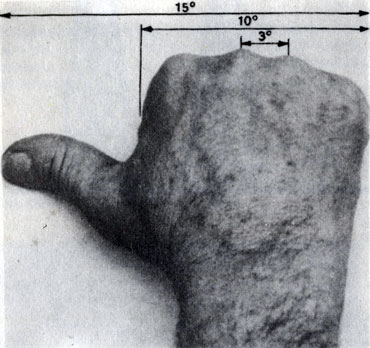
При помощи кулака вытянутой руки легко найти три основных угла. Комбинируя их, можно определять другие углы
И наконец, еще одна угловая мера нашего тела, которая может пригодиться при домашних работах. Угол между большим пальцем и мизинцем растопыренной ладони составляет 90°. Это кажется маловероятным, но вы можете тотчас проверить все сами, приложив растопыренные пальцы ладони к углу нашей книги. Положите мизинец строго параллельно одному краю и двигайте руку вдоль него вниз, пока большой палец также не ляжет на нижний край. Убедились?
Конечно, здесь ошибка порой оказывается сравнительно большой, так как в зависимости от возраста и разработанности кисти большой палец может отставляться на различные расстояния. Но для первого испытания, позволяющего решить, существенно ли отклоняется измеряемый угол от прямого, такой метод вполне пригоден.
ЛАЙНЛАНДИЯ И ФЛАТЛАНДИЯ
Люди, наделенные воображением, уже давно обратили внимание на то, что законы конгруэнтности, столь строгие для двумерного пространства, при применении на практике нередко требуют использования третьего измерения.
Когда сервируют стол к парадному приему гостей, салфетки обычно складывают треугольником. Но стоит собрать эти треугольники в стопку, один на другой, как обнаруживается, что треугольников этих два вида: одни сразу же «подходят» друг к другу, а другие приходится перевернуть «на правильную сторону». Аналогичная проблема возникает и при штамповке мелких деталей, когда кто-нибудь пытается сложить готовую продукцию в штабеля.
Поэтам и писателям свойственно фантазировать вокруг более или менее вероятных ситуаций. Так, существуют произведения, в которых рисуется жизнь в двумерном пространстве (где «салфетку» никак не перевернешь).
Некоторые авторы идут еще дальше и пробуют представить себе жизнь в одномерном пространстве, в Стране Прямой - Лайнландии. Лайнландия населена лишь тоненькими деревянными палочками, которые в простейшем случае ничем друг от друга не отличаются. Однако стоит придать им головки (сразу вспоминаются спички!), и у них тут же появляются две возможности.
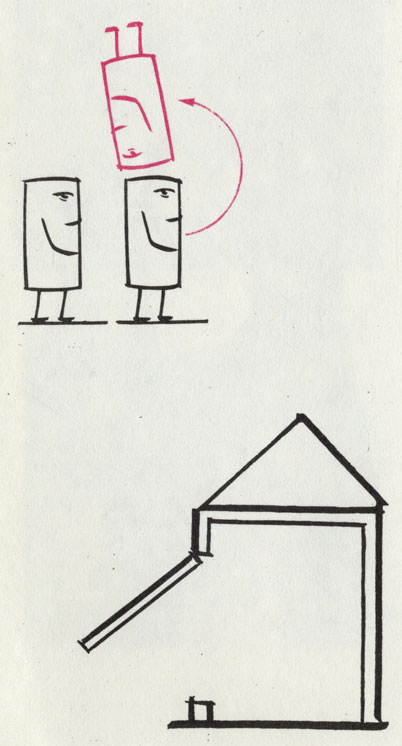
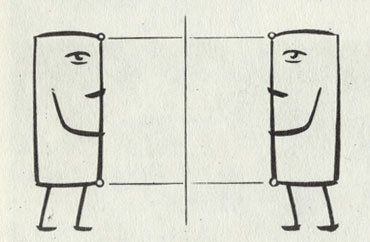
Если флатландцам захочется взглянуть друг на друга, одному из них придется встать на голову. Дома во Флатландии требуют особой конструкции дверей
Либо все спички обращены головками в одну сторону - тогда их совмещение не вызывает сложностей. Либо часть спичек лежит головками налево, а часть - головками направо. Математик из Лайнландии не имеет практической возможности перевести «левые» спички в «правые». Но математик из Страны Плоскости - Флатландии, который располагает еще одним измерением, сразу найдет простое решение: повернет спичку в плоскости.
Однако, по мнению некоторых писателей, жизнь и во Флатландии не так-то проста. Представим себе, что жители этой страны маленькие прямоугольники с глазом (а глаз у них только один) в одном из углов. Видеть такой прямоугольник может, конечно, только в плоскости, и ему никогда не удается взглянуть на эту плоскость сверху. Так что ни один флатландец никогда не сможет представить себе, как на самом деле он выглядит: для этого уже необходим взгляд из трехмерного пространства. Домики у флатландцев были бы примерно такими, как на детских рисунках. С той разницей, что двери находились бы сбоку и открывались бы только в этой же плоскости. Но вот дверные петли пришлось бы делать вне плоскости, выше или ниже ее. Кроме того, понадобилась бы сложная система подпорок, чтобы стена домика не рухнула, когда его обитатели захотели бы открыть дверь. А двое флатландцев смогли бы взглянуть друг на друга лишь в том случае, если бы одному из них удалось встать на голову.
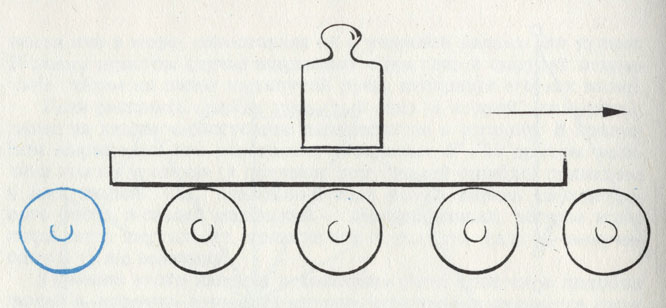
Грузы во Флатландии перевозятся на кругах. Постройка платформы или тележки там невозможна: ведь для устройства оси и ее крепления необходимо третье измерение
Положение усложнилось бы еще больше, если бы Флатландию населяли два народца. Скажем, лево- и правосторонние флатландцы. Требуется большое воображение, чтобы живописать все возможные последствия такой ситуации, особенно если учесть, что мы-то привыкли мыслить в трех измерениях!
Поскольку и Лайнландия, и Флатландия представлялись писателям в юмористическом свете, не приходится удивляться, что литература на эту тему возникла в Англии.
В 1880г. английский педагог Эдвин Эбони Эбботт написал книгу о Флатландии и ее жителях (Эбботт Э. Э. Флатландия. В кн.: Эбботт Э. Э. Флатландия. Бюргер Д. Сферландия. -М.: Мир, 1976). Флатландец Эбботта, попав во сне в Лайнландию, тщетно пытается убедить тамошних обитателей в существовании плоскости.
По ходу действия одному из флатландцев удается познать трехмерное пространство, за что его признают «безумнейшим из безумных».
Через двадцать с лишним лет, в 1907 г., Ч. Г. Хинтон опубликовал роман «Случай во Флатландии». В нем два флатландских народца ведут войну. Поскольку все флатландцы обращены лицом в одну сторону, один из народцев всегда в безнадежном проигрыше: он не может повернуться и нанести ответный удар в нужном направлении - ненавистный враг постоянно сидит у него на шее. Но в конце концов добро побеждает. Какая-то умная голова замечает, что Флатландия расположена на шарике и, значит, можно, обежав вокруг него, зайти врагу в тыл.
Автор романа строит свой рассказ в молчаливом предположении, что флатландцы могут двигаться только по определенным генеральным направлениям, исключающим обход сбоку, а опрокинуть врага через голову для них невозможно.
Как видно, по поводу жизни в двумерном пространстве выдвигались самые изощренные теории, однако они никогда не находили приложения. Надо думать, и эти книги, и их авторы были бы давно позабыты, если бы Лайнландия и Флатландия не были так нужны для пояснения теории зеркального отражения и если бы составителям задач на сообразительность не приходилось все снова и снова обращаться к Флатландии, чтобы извлекать идеи из ее двумерия (кстати, не так давно в Венгрии был создан мультфильм о путешествии школьника Адоляра во Флатландию).
В числе прочего флатландцы перевозят грузы, накатывая платформы на круги. Всякий раз, когда груз минует круг, тамошний транспортный служащий перекатывает этот круг вперед и ставит перед платформой.
Здесь возникает множество любопытных задач. Но нас интересует только одна: если ось колеса движется со скоростью 10 м в минуту, с какой скоростью движется груз?
О нашем земном автомобиле мы знаем, что ни одно колесо (точнее, ни одна колесная ось) не может двигаться скорее, чем весь автомобиль. Но у флатландского автомобился колесо не связано жестко с грузом. Подумав, нетрудно сообразить, что груз здесь участвует в двух движениях.
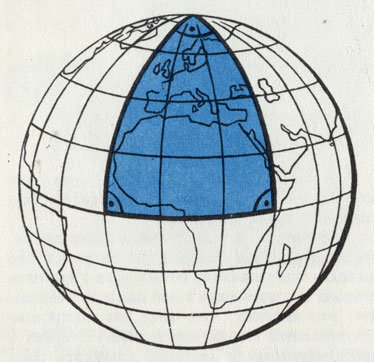
Сумма углов треугольника, расположенного на шаровой поверхности, может превышать 180°
Во-первых, он движется вместе с осью вращения колеса (это так же, как и у автомобиля). А кроме того, груз еще катится по окружности колеса, и при этом со скоростью, тоже равной скорости вращения оси. Следовательно, в целом груз катится с двойной скоростью по отношению к скорости колеса. Разумеется, груз должен двигаться скорее уже потому, что колеса все время остаются позади и их приходится постоянно переставлять вперед.
Некоторые читатели подумают: «Задачка действительно занятная, ну и что из того?»
Однако принцип действия флатландского транспорта находит себе место и в нашей технике. Так, конструктор, проектируя дверь в небольшом помещении (например, у маленького лифта), вынужден отказаться от шарниров. Он делит дверь на две половинки (если, конечно, додумается до такой уловки!), которые ходят параллельно друг перед другом. Одна половинка двери неподвижно скреплена с осью ролика, а вторая двигается по окружности этого ролика. Пока одна половинка сдвигается на половинку ширины двери, другая успевает перебежать всю ширину дверного проема (с удвоенной скоростью).
Не станем смотреть на Флатландию и на писательские фантазии свысока. Предположим, что флатландцы действительно проживают на поверхности шара. Поверхность эта столь велика, что жители могут не заметить ее кривизны. Естественно, они думают, что живут на плоскости, так как шара представить себе не могут: ведь третье измерение им в принципе незнакомо. Поэтому профессора-флатландцы развивают флатландскую математику, которая изучается в школах. Дети там зазубривают, например, такое определение: две параллельные прямые пересекаются на конечном расстоянии. Или: сумма углов треугольника превышает 180°. Мы же, люди трехмерного пространства, знаем, что шаровая поверхность представляет собой двумерное неевклидово пространство, которое не укладывается в привычную евклидову геометрию.
Посмотрев на глобус, мы видим, что два меридиана, параллельные у экватора, на полюсе пересекаются. Глядя на глобус, можно убедиться и в том, что два меридиана образуют с экватором угол 90°. У точки пересечения на полюсе возникает еще один угол. И сумма всех трех углов в любом случае больше 180°. Но бедные флатландцы, конечно, не могут и предположить всего этого. Они-то уверены, что живут на плоскости.
Один скептически настроенный математик, Карл Фридрих Гаусс (1777-1855), всерьез задумался над тем, не в положении ли флатландцев находимся и мы, люди. Возможно, думал Гаусс, мы тоже живем в неевклидовом мире, но только не замечаем этого. Если бы это было так, пространство было бы искривлено (чего бы мы, конечно, не могли себе представить), и у достаточно большого треугольника сумма углов отличалась бы от 180°. Гаусс измерил треугольник между Брокеном, Инзельбергом и Высоким Хагеном, но не нашел существенного отклонения от 180°. Это, конечно, не могло служить бесспорным доказательством, так как треугольник все равно мог оказаться слишком мал.
Впрочем, нельзя просто так сравнивать неевклидово пространство, о котором шла речь, с пространством в теории относительности. Мы с вами, флатландцы и Гаусс ведем речь о чисто геометрической, пространственной проблеме и о том, справедливы ли определенные аксиомы (к примеру, о пересечении двух параллельных прямых в бесконечности). Приверженцы теории относительности в качестве четвертой пространственной координаты вводят время.
О КОНГРУЭНТНОСТИ
Две плоские фигуры конгуэнтны, если у них все углы и отрезки прямых между соответствующими точками равны.
В школе мы изучаем теоремы о конгуэнтно-сти треугольников. Установлено, например, что площади треугольников равны, если у них одна сторона и прилежащие к ней два угла совпадают. Это означает, что, хотя для построения треугольников можно использовать сторону и два прилежащих к ней угла, совпадать треугольники должны всеми своими частями.
В разговорной речи (которой мы и пользуемся в этой книге) можно сказать, что конгруэнтные плоскости точно накладываются друг на друга или, наоборот, если одна плоская фигура точно наложима на другую, то они конгруэнтны. То же самое справедливо и для трехмерных тел: если их можно совместить, то они конгруэнтны.
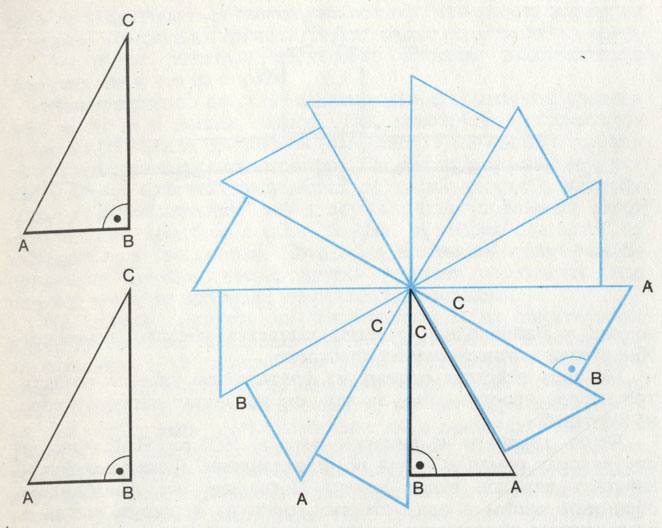
Три изображенных здесь черных треугольника конгруэнтны. Оба левых треугольника можно совместить непосредственно. Правый же треугольник нельзя совместить с левым ни путем простого смещения, ни путем поворота в плоскости листа. Его надо для этого повернуть в пространстве
Посмотрите на треугольники, изображенные на рисунке. Все они конгруэнтны. Очевидно, что оба треугольника, помещенные слева, совместятся, если их попросту передвинуть. А вот треугольник, помещенный справа, хотя и конгруэнтен с двумя левыми, но совместить его с ними только передвижением в плоскости мы не сможем. Как бы мы ни вертели его в плоскости, он никогда не совместится ни с одним из левых треугольников. Чтобы достичь этого, нужно приподнять треугольник над плоскостью, повернуть его в пространстве и снова положить на плоскость. Но если мы сравним взаимное расположение треугольников, совмещенных путем сдвига и перевертывания, то увидим, что в обоих случаях совпадают их разные стороны. При сдвиге нижняя поверхность одного бумажного треугольника накладывается на верхнюю поверхность второго треугольника. Пространственная ориентировка поверхности бумажного листа не изменилась. В этом случае говорят о тождественной конгруэнтности. Если при повороте в пространстве совмещаются обе верхние поверхности бумаги, плоские фигуры называются зеркально-конгруэнтными.
Конгруэнтными называются плоские фигуры, которые мы воспринимаем как равные и которые можно совместить друг с другом путем сдвига в плоскости или поворота в пространстве.
КОНГРУЭНТНОСТЬ ТРЕУГОЛЬНИКОВ
Конгруэнтность - свойство геометрических плоских фигур совпадать между собой по величине и по форме.
Тождественно-конгруэнтными являются фигуры, которые можно совместить друг с другом путем поворота и(или) сдвига.
Зеркально-конгруэнтными являются фигуры, для совмещения которых необходима дополнительно операция зеркального отражения.
Существует четыре признака конгруэнтности треугольников. Треугольники конгруэнтны, если:
1) три стороны одного треугольника равны трем сторонам другого (S, S, S);
2) две стороны и заключенный между ними внутренний угол одного треугольника равны двум сторонам и заключенному между ними внутреннему углу другого треугольника (S, W, S);
3) две стороны и противолежащий большей из них внутренний угол одного треугольника равны двум сторонам и противолежащему большей из них углу другого треугольника (S, S, W);
4) сторона и оба прилежащих к ней внутренних угла одного треугольника равны стороне и обоим прилежащим к ней внутренним углам другого треугольниками (W, S, W).
ПОДОБИЕ
Совпадение плоских фигур по форме, но не по величине называется подобием.
Каждому углу одной из фигур соответствует равновеликий угол подобной фигуры.
В подобных фигурах соответственные отрезки пропорциональны.
Путем сдвига, поворота и (или) зеркального отражения можно привести две подобные фигуры в положение гомотетии. В этом положении соответственные стороны обеих фигур параллельны между собой.
ОСЕВАЯ СИММЕТРИЯ
Пусть плоскость разделена прямой s на две полуплоскости. Если теперь повернуть одну полуплоскость вокруг прямой 5 на 180°, то все точки этой полуплоскости совместятся с точками другой полуплоскости.
Прямая s называется осью симметрии.
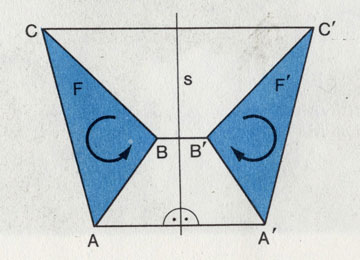
Осевая симметрия
Ввиду того что точки на перевернутой полуплоскости находятся в зеркальном положении по отношению к их первоначальному положению, это переворачивание называют также зеркальным отражением. Если нанести на одну полуплоскость линии, указывающие какие-то направления вращения, то после зеркального отражения это направление изменится на противоположное. Следовательно, одна операция зеркального отражения создает зеркально-конгруэнтные фигуры. Две такие операции приводят к тождественно-конгруэнтным фигурам. Они соответствуют сдвигу, или повороту.
РАДИАЛЬНАЯ СИММЕТРИЯ
Радиально-симметричные фигуры могут быть совмещены друг с другом путем вращения вокруг точки S. Эта точка называется центром симметрии.
При вращении соответственные точки фигур совмещаются. Направление вращения не меняется. Фигура, отраженная таким способом, является тождественно-конгруэнтной.
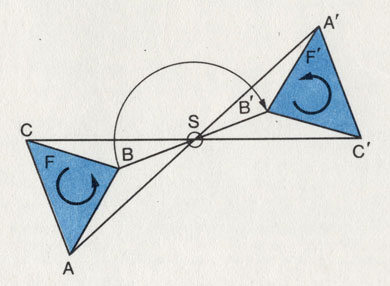
Радиальная симметрия
Последующие операции вращения никак не повлияют на тождественность фигур. При угле поворота, равном 180°, говорят о центральной симметрии.
ТРЮК С КУБИКАМИ
Педагоги утверждают, что игра с кубиками развивает пространственное воображение. И вот родители покупают своим отпрыскам ящики с яркими кубиками, оклеенными фрагментами картинок из популярных сказок. Сложив эти кубики нужным образом, вы увидите Красную Шапочку с Серым Волком или Белоснежку с семью гномами.
На самом деле такого рода кубики и головоломки развивают пространственное воображение не только у детей, но и у всех - от мала до велика. Иногда нам доводится складывать куб из различной формы чурбачков.
При ближайшем рассмотрении этих отдельных элементов оказывается, что по меньшей мере два из них имеют одинаковые форму и размеры, но относятся друг к другу как левая и правая перчатки. Создатели головоломок такого рода, очевидно, надеются, что играющие не сразу уловят это различие. Если припомнить, сколько раз мы путали правые и левые перчатки, придется признать, что такие надежды не лишены основания.
Совместить эти элементы практически невозможно. Следует заметить, что, употребляя здесь (или где-то ниже) выражение «практически возможно», мы имеем в виду осуществление подобного задания на практике.

В машинном отделении корабля двигатели имеют симметричное расположение
Но ведь существуют еще и математические или физические методы, позволяющие совмещать элементы хотя бы теоретически или по внешним признакам, - это и явится предметом дальнейшего рассмотрения. И поскольку здесь говорилось о совмещении одного элемента с другим, следует особо отметить одно важное обстоятельство. Во Флатландии можно было бы совместить плоские фигуры, вынув их из плоскости и повернув в пространстве. В Лайнландии точно так же понадобилось бы всего одним измерением больше: один поворот в плоскости, и отрезки становятся совместимыми.
Но пространственные постройки мы можем повернуть только в пространстве! А поскольку четвертое измерение, несмотря на все рассуждения Гаусса, для нас закрыто, трудно даже вообразить, как практически (!) можно развернуть наши «кирпичики» где-то, помимо трехмерного пространства, чтобы они совместились друг с другом!
В повседневной жизни нам очень часто приходится решать подобные головоломки (я подчеркиваю: именно решать практически, а не играть!), например при упаковке различных предметов. Или, к примеру, представьте себе радиаторы центрального отопления. У одних из них вентиль для регулировки находится слева, у других - справа. Каким образом соединить несколько радиаторов в одну батарею?
Холодильники, кухонные плиты и другие предметы домашнего обихода обычно исполняются с право- и левосторонним расположением ручек, ключей, кранов. Фантастическая возможность поворота подобных предметов в четвертом измерении очень порадовала бы всех, кто имеет дело с их перевозкой и установкой.
ЗАГЛЯНИТЕ В СЛОВАРЬ!
В начале книги мы назвали человека существом симметричным. В дальнейшем же термин «симметрия» больше не употреблялся. Однако вы уже, наверное, заметили, что во всех случаях, когда отрезки прямой, плоские фигуры или пространственные тела были подобными, но без дополнительных действий совместить их было нельзя, «практически» нельзя, мы встречались с явлением симметрии. Эти элементы соответствовали друг другу, как картина и ее зеркальное отражение. Как левая и правая рука. Если мы возьмем на себя труд заглянуть в «Словарь иностранных слов», то обнаружим, что под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра... такое расположение точек относительно точки (центра симметрии), прямой (оси симметрии) или плоскости (плоскости симметрии), при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии...» (Словарь иностранных слов: Изд. 7-е, переработанное. -М.; Русский язык 1980, с. 465)
И это еще не все, как часто бывает с иностранными словами, значений у слова «симметрия» существует множество. В том-то и состоит преимущество подобных выражений, что их можно использовать в случае, когда не хотят дать однозначное определение или просто не знают четкого различия между двумя предметами.

При всей прихотливости формы цветок орхидеи симметричен
Термин «соразмерный» мы применяем по отношению к человеку, картине или какому-либо предмету, когда мелкие несоответствия не позволяют употребить слово «симметричный».
Раз уж мы роемся в справочниках, давайте заглянем в Энциклопедический словарь (Советский энциклопедический словарь - М.: Советская энциклопедия, 1980, с. 1219-1220). Мы обнаружим здесь шесть статей, начинающихся со слова «симметрия». Кроме того, это слово встречается во множестве других статей.
В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения. Важную роль играет симметрия в кристаллографии (кое-что об этом вы еще прочтете в этой книге). Интересно интерпретируется понятие симметрии в биологии. Там описывается шесть различных видов симметрии. Мы узнаем, например, что гребневики дисимметричны, а цветки львиного зева отличаются билатеральной симметрией. Мы обнаружим, что симметрия существует в музыке и хореографии (в танце). Она зависит здесь от чередования тактов. Оказывается, многие народные песни и танцы построены симметрично.

Цветы кальцеолярии симметричны. Ось симметрии проходит вдоль стебля
Итак, надо договориться, о какой именно симметрии пойдет у нас речь. Независимо от характера рассматриваемых предметов основной интерес для нас будет представлять зеркальная симметрия - симметрия левого и правого. Мы увидим, что это кажущееся ограничение уведет нас далеко в мир науки и техники и позволит время от времени подвергать испытанию способности нашего мозга (так как именно он запрограммирован на симметрию).
ИГРА В ТОЧКИ И ЛИНИИ
Мы еще не ушли от Лайнландии и Флатландии. И на то есть особая причина. Если даже там и нет обитателей, то сами-то прямые и плоскости вполне реальны!
Поразмыслим, как обстоит с симметрией на прямой. С помощью двух спичек мы можем очень просто представить себе два возможных случая. (Некоторые стороны этой ситуации мы уже рассмотрели раньше.) Спички могут лежать головками в одну сторону. Тогда они легко совмещаются. Или же головками (или кончиками) друг к другу. В этом случае на прямой существует точка, в которой зеркало можно поставить таким образом, что наступит кажущееся совмещение спички со своим отражением. Другими словами, на прямой существует центр симметрии. Нам придется представить, что зеркало уместилось в одной точке и в нем отражается половинный отрезок прямой. В математических рассуждениях это вполне возможно.
Плоские фигуры 'отражаются' в осях симметрии
При построениях на плоскости наше зеркало может по-прежнему оставаться точкой, а может быть и прямой. Наверное, правильнее сказать в обратном порядке: зеркалом будет служить прямая или точка. Ведь если где-то есть прямая, то на ней возможен точечный центр симметрии.
Зеркальные отражения половинок плоскостей выглядят так же, как и реальные плоскости: путем поворота плоскости вокруг прямой - зеркала - ее можно совместить с отражением, отсюда и возникло выражение «ось симметрии».
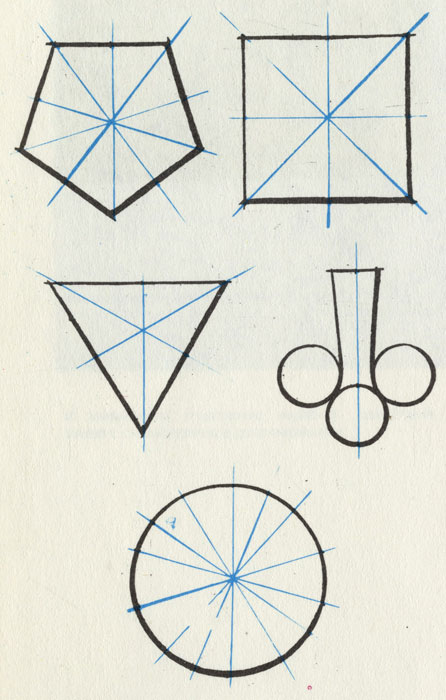
Круг имеет бесконечное множество осей симметрии. 'Лист клевера' - только одну
Итак, мы знаем теперь, что представляют собой центр симметрии и ось симметрии, а также то, что какой-то предмет (возьмем это нейтральное слово) является симметричным, если одна его половина соотносится с другой, как изображение и его зеркальное отражение.
У круга имеется бесконечное множество осей симметрии, и все они проходят через общий центр симметрии. У других фигур число осей симметрии конечно, но все равно все оси (две их или больше) проходят через центр симметрии. Это значит, что мы можем развернуть фигуру на какой-то определенный угол (максимально на 180°) и она снова ляжет точно на то же место, что и до вращения.
Продолжим свои рассуждения о зеркальной симметрии. Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична. Сначала представляется, что параллельно одной из его сторон могла бы проходить ось симметрии. Но стоит мысленно попробовать воспользоваться ею, как сразу убеждаешься, что это не так. Несимметрична и спираль.
Как ни странно, такая 'симметричная' с виду фигура, как параллелограмм, не имеет не только осей симметрии, но и зеркальной симметрии вообще
В то время как симметричные фигуры полностью соответствуют своему отражению, несимметричные отличны от него: из спирали, закручивающейся справа налево, в зеркале получится спираль, закручивающаяся слева направо. Это свойство нередко используется в массовых играх и соревнованиях, проводимых телевидением. Играющим предлагается, глядя в зеркало, нарисовать какую-либо несимметричную фигуру, например спираль. А потом еще раз нарисовать «точно такую же» спираль, но уже без зеркала. Сравнение обоих рисунков показывает, что спирали получились разные: одна закручивается слева направо, другая - справа налево.
Но то, что здесь выглядит шуткой, в практической жизни доставляет массу сложностей не только детям, но и взрослым. Нередко дети пишут некоторые буквы «навыворот». Латинское N выглядит у них как И, вместо S и Z получается S и Z. Если мы внимательно посмотрим на буквы латинского алфавита (а это ведь тоже, в сущности, плоские фигуры!), то увидим среди них симметричные и несимметричные. У таких букв, как N, S, Z, нет ни одной оси симметрии (равно как и у F, G, J, L, Р, Q и R). Но N, S и Z особенно легко пишутся «наоборот» (Они обладают центром симметрии. - Прим. ред). У остальных прописных букв есть как минимум по одной оси симметрии. Буквы А, М, Т, U, V, W и Y можно разделить пополам про дольной, осью симметрии. Буквы В, С, D, Е, I, К - поперечной осью симметрии. У букв Н, О и X имеется по две взаимно перпендикулярные оси симметрии.

Буквы в трех верхних рядах асимметричны. У остальных букв имеется по меньшей мере одна ось симметрии
Если вы поместите буквы перед зеркалом, расположив его параллельно строке, то заметите, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».

И в природе, и в архитектуре оси симметрии служат опорными элементами или элементами стиля. Раковина
Вопрос, почему буквы с продольной осью ведут себя иначе, чем с поперечной, довольно интересен. Возможно, и вы задумаетесь над ним. Причину этого явления мы еще обсудим в дальнейшем.

И в природе, и в архитектуре оси симметрии служат опорными элементами или элементами стиля. Морской еж
Встречаются дети, которые пишут левой рукой, и все буквы получаются у них в зеркальном, отраженном, виде. «Зеркальным шрифтом» написаны дневники Леонардо да Винчи. Вероятно, не существует веского основания, заставляющего нас писать буквы именно так, как это делаем мы. Вряд ли зеркальным шрифтом труднее овладеть, чем нашим обычным.

И в природе, и в архитектуре оси симметрии служат опорными элементами или элементами стиля. Гавана
Правописание от этого не стало бы проще, а некоторые слова, как, например, ОТТО, вообще не изменились бы. Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф розначает именно истинную середину.

И в природе, и в архитектуре оси симметрии служат опорными элементами или элементами стиля. Дворец и парк Сан-Суси
В архитектуре оси симметрии используются как средства выражения архитектурного замысла. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля.
НАШ МИР В ЗЕРКАЛЕ
Из Лайнландии мы вынесли представление о центре симметрии, а из Флатландии - об оси симметрии. В трехмерном мире пространственных тел, где мы с вами живем, соответственно существуют плоскости симметрии. «Зеркало» всегда имеет на одно измерение меньше, чем мир, который оно отражает. При взгляде на круглые тела сразу видно, что они имеют плоскости симметрии, но вот сколько именно - решить не всегда просто.
Поставим перед зеркалом шар и начнем его медленно вращать: изображение в зеркале никак не будет отличаться от оригинала, конечно в том случае, если шар не имеет каких-либо отличительных признаков на своей поверхности. Шарик для пинг-понга обнаруживает бессчетное множество плоскостей симметрии. Возьмем нож, отрежем половину шара и поместим ее перед зеркалом. Зеркальное отражение вновь дополнит эту половинку до целого шарика.
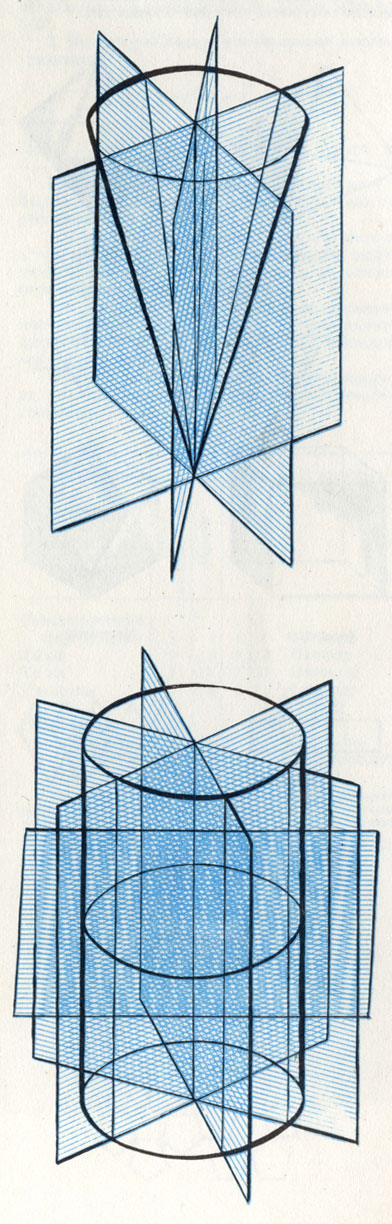
Симметричные тела имеют одну или несколько плоскостей симметрии. Шар или тело, основанием которого служит полусфера или круг, имеет бесконечное множество плоскостей симметрии
Но если мы возьмем глобус и рассмотрим его симметрию, учитывая нанесенные на нем географические контуры, то мы не отыщем ни одной плоскости симметрии.
Во Флатландии фигурой с бесчисленным множеством осей симметрии был круг. Поэтому нас не должно удивлять, что в, пространстве аналогичные свойства присущи шару. Но если круг является единственным в своем роде, то в трехмерном мире имеется целый ряд тел, обладающих бесконечным множеством плоскостей симметрии: прямой цилиндр с кругом в основании, конус с круговым или полусферическим основанием, шар или сегмент шара. Или возьмем примеры из жизни: сигарета, сигара, стакан, конусообразный фунтик с мороженым, кусочек проволоки, труба.
Если мы повнимательней присмотримся к этим телам, то заметим, что все они так или иначе состоят из круга, через бесконечное множество осей симметрии которого проходит бесчисленное множество плоскостей симметрии. Большинство таких тел (их называют телами вращения) имеют, конечно, и центр симметрии (центр круга), через который проходит по меньшей мере одна ось симметрии.
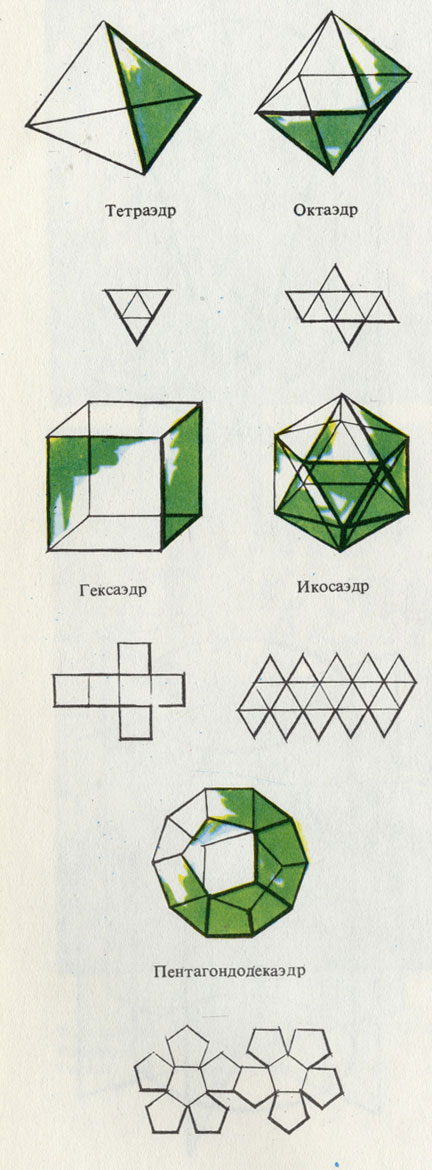
Из правильных конгруэнтных плоских фигур можно построить пять Платоновых тел
Отчетливо видна, например, ось у конуса фунтика с мороженым. Она проходит от середины круга (торчит из мороженого!) до острого конца конуса-фунтика. Совокупность элементов симметрии какого-либо тела мы воспринимаем как своего рода меру симметрии. Шар, без сомнения, в отношении симметрии является непревзойденным воплощением совершенства, идеалом. Древние греки воспринимали его как наиболее совершенное тело, а круг, естественно, как наиболее совершенную плоскую фигуру.
В целом эти представления вполне приемлемы и по сей день. Далее греческие философы делали вывод о том, что Вселенная, несомненно, должна быть построена по образцу математического идеала. Из этого заключения проистекали ошибки, о последствиях которых мы еще расскажем. Ясно, что у древних греков еще не было фунтиков с мороженым! Иначе бы такой прозаический предмет, имеющий бесчисленное множество плоскостей симметрии, мог бы нарушить их стройную систему.
Если для сравнения мы рассмотрим куб, то увидим, что он имеет девять плоскостей симметрии. Три из них делят его грани пополам, а шесть проходят через вершины. По сравнению с шаром это, конечно, маловато.
А имеются ли тела, занимающие по числу пло.скостей промежуточное положение между шаром и кубом? Без сомнения - да. Стоит только вспомнить, что круг, в сущности, как бы состоит из многоугольников. Мы проходили это в школе при вычислении числа π. Если над каждым n-угольником мы воздвигнем n-угольную пирамиду, то сможем провести через нее n плоскостей симметрии.
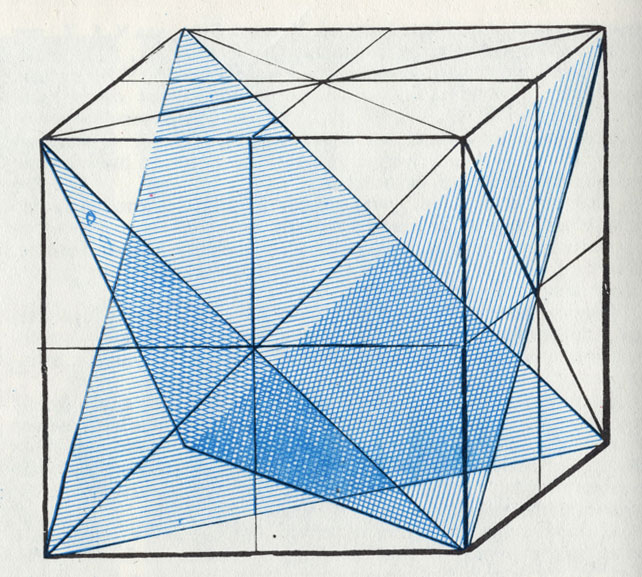
Куб располагает девятью плоскостями симметрии
Можно было бы придумать 32-гранную сигару, которая имела бы соответствующую симметрию!
Но если мы тем не менее воспринимаем куб как более симметричный предмет, чем пресловутый фунтик с мороженым, то это связано со строением поверхности. У шара поверхность всего одна. У куба их шесть - по числу граней, и каждая грань представлена квадратом. Фунтик с мороженым состоит из двух поверхностей: круга и конусообразной оболочки.
Более двух тысячелетий (вероятно, благодаря непосредственному восприятию) традиционно отдается предпочтение «соразмерным» геометрическим телам. Греческий философ Платон (427-347 до н. э.) открыл, что из правильных конгруэнтных плоских фигур можно построить только пять объемных тел.
Из четырех правильных (равносторонних) треугольников получается тетраэдр (четырехгранник). Из восьми правильных треугольников можно построить октаэдр (восьмигранник) и, наконец, из двадцати правильных треугольников - икосаэдр. И только из четырех, восьми или двадцати одинаковых треугольников можно получить объемное геометрическое тело. Из квадратов можно составить только одну объемную фигуру - гексаэдр (шестигранник), а из равносторонних пятиугольников - додекаэдр (двенадцатигранник).
А что в нашем трехмерном мире полностью лишено зеркальной симметрии?
Если во Флатландии это была плоская спираль, то в нашем мире таковыми, безусловно, будут винтовая лестница или спиральный бур. Кроме того, существуют еще тысячи асимметричных вещей и предметов в окружающей нас жизни и технике. Как правило, винт имеет правую резьбу. Но иногда встречается и левая. Так, для большей безопасности баллоны с пропаном снабжены левой резьбой, чтобы к ним нельзя было привинтить вентиль-редуктор, предназначенный, например, для баллона с другим газом. В повседневной жизни это означает, что в кемпинге, прежде чем готовить на походной плитке, надо всегда попробовать, в какую сторону отвинчивается баллон.
Между шаром и кубом, с одной стороны, и винтовой лестницей, с другой, существует еще масса степеней симметрии. От куба можно постепенно отнимать плоскости симметрии, оси и центр, пока мы не придем к состоянию полной асимметрии.
Почти у конца этого ряда симметрии стоим, мы, люди, с всего единственной плоскостью симметрии, разделяющей наше тело на левую и правую половины. Степень симметрии у нас такая же, как, например, у обычного полевого шпата (минерала, образующего вместе со слюдой и кварцем гнейс или гранит).
ПЯТЬ ПЛАТОНОВЫХ ТЕЛ
Для правильных многогранников справедливы следующие утверждения:
1. В любом многограннике (в том числе и правильном) сумма всех углов между ребрами, сходящимися в одной вершине, всегда меньше 360°.
2. По теореме Эйлера для выпуклых многогранников
e+ƒ-k=2,
где е - число вершин, ƒ - число граней и k - число ребер.
Гранями правильных многогранников могут быть лишь следующие правильные многоугольники:
3, 4 или 5 равносторонних треугольников с углом 60°. Шесть таких треугольников дают уже 60° Х 6 = 360° и, следовательно, не могут ограничивать многогранный угол.
Три квадрата (90° X 3 = 270°), 3 правильных пятиугольника (108° X 3 = 324°), 3 правильных шестиугольника (120° X 3 = 360°) ограничивают многогранный угол.
Из теоремы Эйлера и формы граней следует, что существует только 5 правильных многогранников:
| Формы граней | Число | Платоновы тела | |||
| граней в одной вершине | вершин | граней | ребер | ||
| Равносторонние треугольники | 3 | 4 | 4 | 6 | Тетраэдр |
| То же | 4 | 6 | 8 | 12 | Октаэдр |
| То же | 5 | 12 | 20 | 30 | Икосаэдр |
| Квадраты | 3 | 8 | 6 | 12 | Гексаэдр (куб) |
| Правильные пятикгольники | 3 | 20 | 12 | 20 | Пентагон-додекаэдр |
(Любая грань Пентагон-додекаэдра представляет собой пятиугольную фигуру, у которой четыре стороны равны между собой, но отличны от пятой. - Прим. перев)
https://glamour-models.ru законно ли работать веб моделью работа веб моделью.
|
ПОИСК:
|