КАК ОТРАЖАЕТ ЗЕРКАЛО? [1982 Гильде В.

Конечно, все мы знаем, как отражает зеркало, но, если только потребуется описать это точно, несомненно возникнут трудности. Как правило, мы довольны собой, если что-то представляем себе хотя бы «в принципе». А подробности, которые преподаватели физики объясняли нам на доске с помощью мела и линейки, всякий нормальный школьник и студент стараются забыть, и, чем скорее, тем лучше.

Каждый ребенок, исполненный удивления перед окружающим миром, непременно заинтересуется, каким образом зеркало отражает его. Но взрослые обычно отвечают в подобных случаях: «Не задавай глупых вопросов!» Человек сникает, начинает стесняться, удивление его постепенно затухает, и он старается больше не проявлять его до конца жизни (а жаль!).

Но в этой книге мы будем как можно больше удивляться, памятуя о словах Бертольда Брехта: «Глупых вопросов не бывает, бывают только глупые ответы».

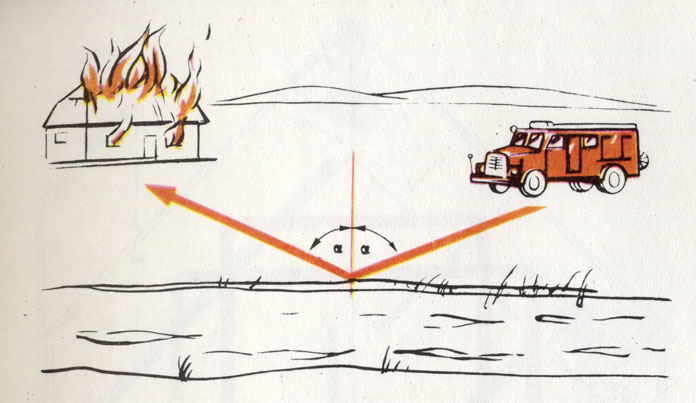
Какой путь от горящего дома до стоянки пожарной команды кратчайший? 'Угол падения', под которым пожарная машина достигнет реки, должен быть равен 'углу отражения', под которым она помчится к месту пожара

Конечно, людей можно разделить на дураков и умных, на больших и маленьких, они разнятся по языку, вероисповеданию, мировоззрению. Можно представить себе и такой способ подразделения:

2) люди, которые удивляются, но не задумываются над удивившим их явлением;

3) люди, которые, удивившись, спрашивают «а почему?»;

4) люди, которые, удивившись, обращаются к числу и мере.

В зависимости от условий жизни, традиций, степени образованности встречаются и все возможные «промежуточные» ступени. Мыслители античности и средневековья изумлялись миру и думали о его тайнах. Но им лишь изредка выпадал случай измерить какое-либо явление.

Только в эпоху Возрождения, то есть в XVI в., люди пришли к убеждению, что измерение лучше слепой веры или схоластических рассуждений. Этому способствовали экономические интересы, удовлетворить которые можно было только путем развития естественных наук, путем количественных измерений. (Мы видим, что, по существу, меновая стоимость «измерялась» с помощью денег.) Для XVI в. оптика была ультрасовременной наукой. Из стеклянного шара, наполненного водой, которым пользовались как фокусирующей линзой, возникло увеличительное стекло, а из него микроскоп и подзорная труба. Крупнейшей в те времена морской державе Нидерландам требовались для флота хорошие подзорные трубы, чтобы загодя рассмотреть опасный берег или вовремя уйти от врага. Оптика обеспечивала успех и надежность навигации. Поэтому именно в Нидерландах многие ученые занимались ею. Голландец Виллеброрд, Снелль ван Ройен, именовавший себя Снеллиусом (1580-1626), наблюдал (что, впрочем, видели и многие до него), как тонкий луч света отражается в зеркале. Он просто измерил угол падения и угол отражения луча (чего до него не делал никто) и установил закон: угол падения равен углу отражения.

Для построения зеркального отражения необходимо соблюдать закон: угол падения равен углу отражения

Теперь, задним числом, этот закон кажется нам чем-то само собой разумеющимся. Но в те времена он имел огромное, можно сказать, мировоззренческое значение, которое будило философскую мысль вплоть до XIX в.

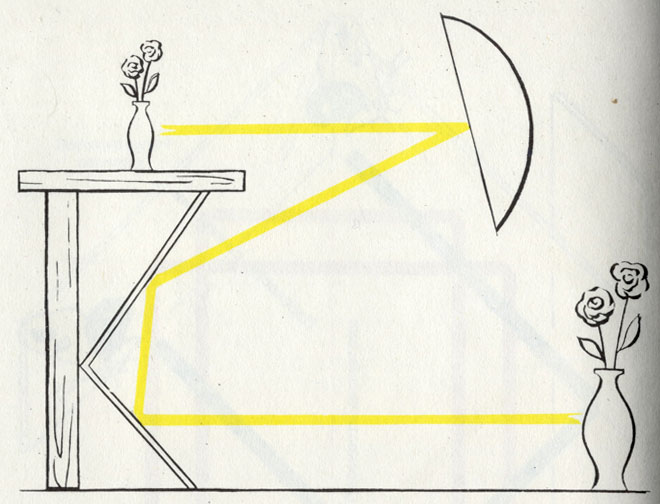
Поставим себе следующую математическую задачу: в каком-то домике возник пожар. Вызвана пожарная команда, а воду для тушения приходится брать из реки. В каком месте следует ее набирать, чтобы как можно быстрее подать к горящему дому?

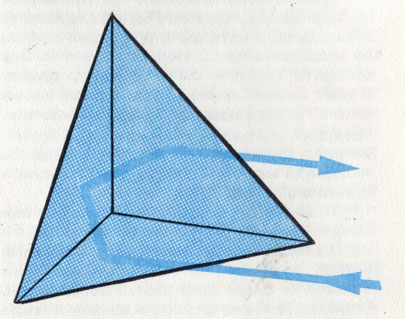
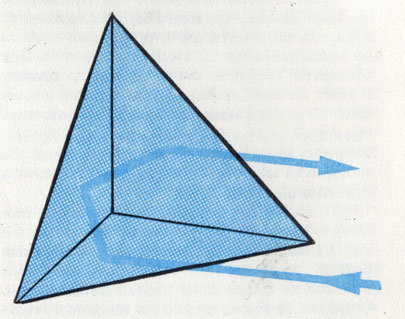
Треугольное зеркало отбрасывает отраженный луч точно в направлении падающего луча

Ответ гласит: место надо выбрать с таким расчетом, чтобы угол подъезда к реке был равен углу отъезда от нее по прямой к горящему дому. В этом случае общая длина отрезков пути будет минимальной. (Такой принцип минимума-максимума прежде рассматривался как проявление «воли господней»).

Закон отражения Снеллиуса объясняет явление зеркального отражения, к этому только следует добавить, почему оно свойственно лишь блестящим и гладким поверхностям. На самом деле шершавые поверхности тоже подчиняются закону отражения. Но вследствие шероховатости они словно состоят из маленьких зеркал, бессистемно направленных во все стороны. Кроме того, материал, который мы рассматриваем как зеркало, должен в очень малой мере поглощать свет и не быть прозрачным. Такими качествами отличаются, к примеру, полированные металлы, спокойная вода над темным дном, некоторые полированные камни и прежде всего помещенное на непрозрачную подложку стекло.

Мачты яхт оснащают уголковыми зеркальными отражателями. Маленькое трехгранное зеркало отражает импульс радара гораздо сильнее, чем корпус судна

Каждой точке предмета соответствует ее отражение в зеркале, и потому в нем наш правый глаз перемещается на левую сторону. Вследствие этого переноса точек предметы, расположенные дальше, в зеркале тоже кажутся уменьшенными в соответствии с законами перспективы. Технически мы можем реконструировать зеркальное изображение так, словно оно расположено за поверхностью стекла. Но это только кажущееся восприятие. Не случайно животные и маленькие дети часто заглядывают за зеркало; они верят, что изображение таится сзади, словно картина, видимая за окном. Факт перестановки левого и правого правильно осознается только взрослыми.

В одном из греческих мифов повествуется о Нарциссе, который часами лежал на берегу озера, любуясь своим отражением в воде.

Однако в дальнейшем производство зеркал скорее всего пойдет по пути использования пластиковой пленки, на которую напыляется тонкий слой металла.

Должны ли мы считать, что самих себя видим только в «зеркальном отражении» и в лучшем случае лишь на фото и кинопленке можем узнать, как выглядим «на самом деле»?

Конечно нет: достаточно зеркальное изображение вторично отразить в зеркале, чтобы увидеть свое истинное лицо. Нередко в домах еще встречаются так называемые трельяжи. Они имеют одно большое главное зеркало в црнтре и два меньших зеркала по сторонам. Многие думают, что эти боковые зеркала служат лишь для того, чтобы разглядывать локоны за ушами. Но если такое боковое зеркало поставить под прямым углом к среднему, то можно увидеть себя именно в том виде, в каком вас видят окружающие. Зажмурьте левый глаз, и ваше отражение во втором зеркале повторит ваше движение левым глазом. Перед, трельяжем вы можете выбирать, хотите ли вы увидеть себя в зеркальном или в непосредственном изображении.

Угловое зеркало с прямым углом между составляющими его зеркалами отличается еще некоторыми интересными свойствами. Если вы смастерите его из двух маленьких зеркал, то сможете сами убедиться в том, что в таком зеркале с прямоугольным раствором (а сейчас мы говорим только о нем) отраженный луч света всегда параллелен падающему лучу. Это очень важное свойство. Но не единственное! При повороте углового зеркала вокруг оси, соединяющей зеркала (в определенных пределах), отраженный луч не изменит своего направления.

В технике обычно не составляют зеркала, а используют прямоугольную призму, у которой соответствующие грани обеспечивают зеркальный ход лучей.

Прямоугольные призмы, как бы «складывающие» ход луча «гармошкой», сохраняя его необходимую длину, заданную фокусным расстоянием линзы, позволяют уменьшать габариты оптических приборов. В призматических биноклях лучи света при помощи таких приборов обращаются на 180°.

На старинных картинах можно видеть капитанов и полководцев с непомерно длинными подзорными трубами. Благодаря угловым зеркалам старинные подзорные трубы превратились в современные бинокли.

Принцип действия Танагрского театра. Благодаря зеркалам создается впечатление, что на сцене движутся маленькие человечки или предметы, как бы наблюдаемые в перевернутый бинокль

Игрокам в бильярд издавна знакомо действие отражения. Их «зеркала» - это борта игрового поля, а роль луча света исполняют траектории шаров. Ударившись о борт возле угла, шар катится к стороне, расположенной под прямым углом, и, отразившись от нее, движется обратно параллельно направлению первого удара.

Свойство отраженного луча сохранять направление при повороте углового зеркала вокруг оси находит широкое применение в технике. Так, в трехгранном зеркальном уголковом отражателе луч сохраняет постоянное направление, несмотря на весьма сильные качания зеркала. По форме такое зеркало представляет собой кубик с отрезанным уголком. И в этом случае на практике используют не три зеркала, а соответствующую стеклянную призму с зеркальными гранями.

Важной областью применения трехгранного зеркала служит уголковый отражатель (кошачий глаз, катофот) на велосипедах, мотоциклах, сигнальных предохранительных щитах, ограничителях проезжей части улицы. С какой бы стороны ни упал свет на такой отражатель, световой рефлекс всегда сохраняет направление источника света.

Большую роль трехгранные зеркальные уголковые отражатели играют в радиолокационной технике. Самолеты и крупные стальные корабли отражают луч радара. Несмотря на значительное рассеяние его, той небольшой доли отраженных радиоволн, которая возвращается к радару, обычно достаточно для распознания объекта.

Хуже обстоит дело с маленькими суденышками, сигнальными поплавками и пластиковыми парусными яхтами. У небольших предметов отражение слишком слабое. Пластиковые яхты так же «прозрачны» для радиоволн, на которых работает радарная техника, как оконные стекла для солнечного света. Поэтому парусные яхты и сигнальные буйки оснащают металлическими уголковыми отражателями. Длина граней у такого «зеркала» всего около 30 см, но этого довольно, чтобы возвращать достаточно мощное эхо.

Художественные изделия из стекла производят впечатление не только благодаря совершенству формы и тщательной шлифовке, но и благодаря высокому показателю преломления стекла

Вернемся еще раз к угловому зеркалу из двух соединенных зеркал. Качнем его ось вправо или влево - наше изображение тоже наклонится в сторону. Мы можем даже положить его, если поместим ось зеркала горизонтально. Но, наклонив зеркало еще дальше, мы заметим, что изображение «выпрямляется». Конечно, и этому мы поищем объяснение. Оно вполне отвечает теме этой книги.

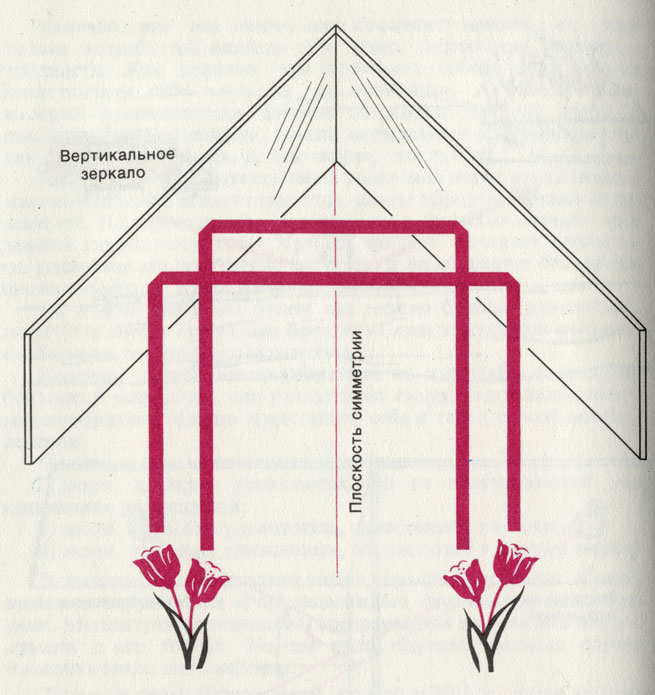
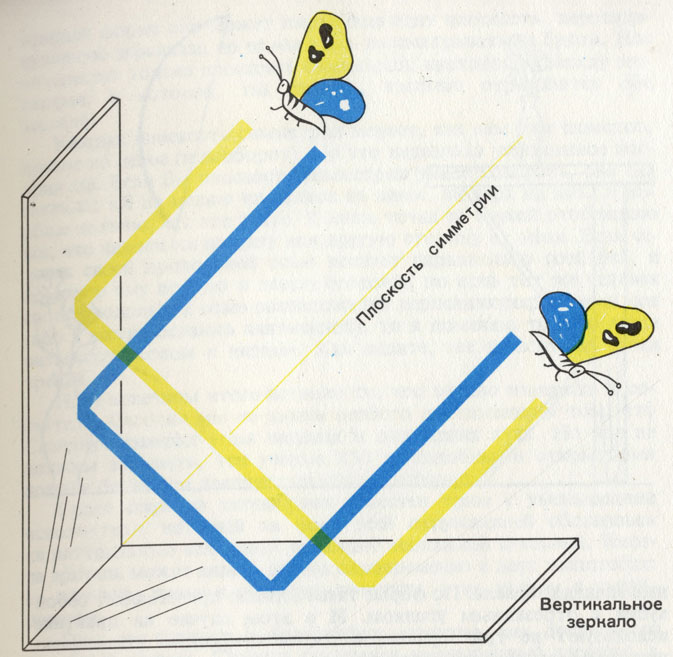
Угловое зеркало имеет плоскость симметрии, которая делит пополам пространство между обоими зеркалами. При соответствующей форме оно может иметь еще одну плоскость, перпендикулярную зеркалам, но ее мы здесь рассматривать не будем. Нас интересует только плоскость симметрии, проходящая между зеркалами в которой, так сказать, взаимно отражаются оба зеркала.

Каждая плоскость симметрии меняет, как нам уже известно, правое на левое (и наоборот). Но это несколько упрощенное вос-риятие. Если бы плоскость симметрии умела говорить, она бы заявила: «Я не меняю ни правое на левое, ни верх на низ. Я вообше не знаю, что это такое. Я лишь точка за точкой отображаю все, что находится по одну или другую сторону от меня. Если человек своей продольной осью встанет параллельно соей оси, я поменяю ему правую и левую стороны, но если тот же человек своей продольной осью расположится перпендикулярно моей оси (ибо я всегда остаюсь неизменной), то я поменяю то, что люди называют верхом и низом». Как видите, все зависит от точки зрения.

Но в конечном итоге истинно то, что можно измерить и сосчитать. Сегодня мы не видим особого достижения в том, что Снеллиус измерил углы падения и отражения луча. Но мы не должны забывать, что ученые XVI в. подобными открытиями ломали более чем двадцативековую традицию.

Среди секретов телевидения известен трюк с уменьшением исполнителя, который на фоне всей окружающей обстановки «в натуральную величину» выглядит маленькой куколкой. Иногда зритель может видеть актера одновременно в двух масштабах: на переднем плане в обычную величину, а на заднем в уменьшенном.

Тому, кто искушен в фотографии, понятно, как достигается подобный эффект. Сначала снимается уменьшенный вариант, а потом актер играет перед экраном, на который проецируется его уменьшенное изображение.

Известный «чародей» Иохен Цмек в своей увлекательной книге «Волшебный мир магии» (Zmeck J. Wunderwelt Magie. Berlin: Heuchel-Verlag, Kunst und Gesellschaft, 1974) описывает, как подобные чудеса можно делать без фотографии. Когда уменьшенный предмет должен сам собой появиться в пространстве, с помощью вогнутого зеркала его изображение проецируется таким образом, чтобы он казался стоящим на подставке.

Иллюзионист Александр Фюрст строил этот трюк следующим образом. Зритель видел маленькую сцену с сильно уменьшенными артистами. Чтобы спроецировать их в таком виде на экран, Фюрст использовал в своем сооружении угловое зеркало. Именно перед ним двигались артисты. Но зеркало переворачивало их на 180° и ставило тем самым «на голову», и уже это изображение вогнутое зеркало, еще раз перевернув, отбрасывало на маленькую сцену. Непременным условием эффекта была безупречная чистота всех зеркал.

Разумеется, «волшебник» мог демонстрировать не только появление каких-то предметов, но и их молниеносное исчезновение, стоило только произнести магическое «симсалабим» (и, конечно, выключить источник света или отвернуть зеркало). Как прелестен такой Танагрский театр (так называются подобные зрелища), можно убедиться, заглянув в перевернутый бинокль. Уменьшенный, как бы сконцентрированный мир выглядит в нем очень интересно. Принцип действия и призматического бинокля, и Танагрского театра одинаков. Только в одном случае используются линзы, а в другом - вогнутое зеркало.

Теперь, когда мы знаем, как работают зеркала и как они изготовляются, подумаем еще над тем, что же мы видим в зеркале в нашей повседневной жизни.

Это может превратиться в хобби: анализировать каждый предмет с точки зрения симметрии. Вспомним о том, что если разрезать предмет вдоль его плоскости симметрии и поставить одну из половинок перпендикулярно зеркалу, то в зеркале как бы появится вторая, «отрезанная» половина. Поэтому, говорим ли мы о зеркале или о плоскости симметрии, речь идет, в сущности, о явлениях одного порядка.

В принципе все возможные «волшебные» оптические трюки основаны на «бесшовном» переходе изображения в его зеркальное отражение. Секрет «разрезанной пополам дамы» и прочих подобных фокусов вы можете легко постичь и воспроизвести, пользуясь трельяжем, состоящим из нескольких зеркал. Поверните одно из малых зеркал внутрь настолько, чтобы его хорошо было видно в большом зеркале. Положите руку на край малого зеркала так, чтобы средний палец лег параллельно краю, и вы увидите в зеркале, что ваша рука состоит из двух мизинцев и двух безымянных пальцев. Оттопырьте мизинец, и в зеркале шевельнутся два пальца. Немного фантазии - и этот «номер» можно подготовить для демонстрации на домашнем вечере. Условие успеха здесь, как и в варьете или цирке, состоит в безупречной чистоте зеркала. Хорошее и достаточно большое зеркало (чтобы не было видно его краев) для глаз не заметно.

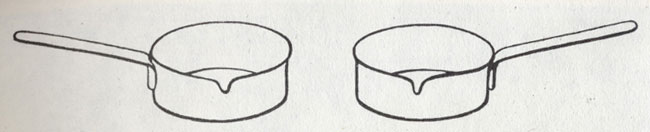
Ковшики всегда выпускаются с расчетом, что их будут брать правой рукой. Но всякий левша предпочел бы ковшик в 'зеркальном' исполнении

После того как мы мысленно разделим плоскостями симметрии стулья, столы, вазы, людей, животных, дома и деревья, нам, конечно, захочется поискать асимметричные тела.

О винтовых лестницах и винтовой нарезке мы уже упоминали. Пожалуй, следует еще раз уточнить свойство асимметрии: через асимметричный предмет нельзя провести плоскость симметрии (Автор здесь относит к симметричным лишь те тела, которые обладают плоскостями симметрии. В современном учении о симметрии к симметричным телам относят все фигуры, состоящие из равных закономерно повторяющихся частей. В частности, и фигуры с винтовыми линиями, рассматриваемые как бесконечно протяженные системы, обладают винтовыми осями симметрии, то есть считаются симметричными. - Прим. ред). Поэтому его невозможно «правильно» отразить в зеркале. И наоборот: каждая спираль закручивается в зеркале «в другую сторону». Левый виток становится правым. Левая рука превращается в правую. Может быть, отсюда и пошли слова «левша» и «правша»?

Однако здесь может возникнуть возражение: как же у человека, существа, наделенного плоскостью симметрии, могут «поменяться» в зеркале руки или уши?!

Для того чтобы разобраться, представьте, что в зеркале видна только рука, без ее владельца. Вы можете сами попробовать, встав боком к зеркалу, поместить перед ним одну руку. Или попросту рассмотрите внимательно ваши перчатки. Они соотносятся друг с другом, как изображение и его зеркальное отражение. А вот если вы разрежете посередине кубик, то не различите половинки! Они совмещаются (мысленно) безо всякого труда.

Поищем дальше, какие еще асимметричные предметы окружают нас. Бывают ли чашки для левшей? Или ножницы для тех, кто режет левой рукой?

У чашки поверхность симметрична: из нее можно пить и справа и слева. Но вот наши деды пользовались особыми чашками для усачей. Сверху такая чашка имела козырек, чтобы гордые усы не окунались в кофе. Отверстие, через которое наполняли чашку и пили, находилось с одной стороны. Такая чашка уже не симметрична. Она делалась либо для левой, либо для правой руки.

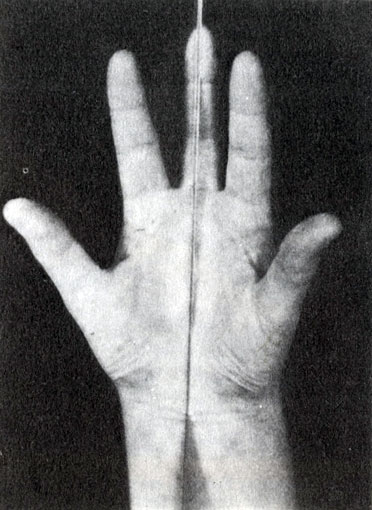
Если положить средний палец вдоль края зеркала и пошевелить указательным пальцем, в зеркале возникнет забавное отражение

Ножницы, как правило, делаются для правой руки. Вы сразу аметите это, как только попытаетесь остричь на ней ноготь, в ножницы в левую руку. Ковшики тоже всегда делаются для правой руки. Среди сувенирной мелочи иногда как курьез продаются штопоры для левой руки: ведь левше очень неудобно открывать бутылку нормальным штопором. Асимметричны, конечно, такие предметы, как винт корабля или самолета. Прежде большие гидропланы имели два пропеллера: тянущий и толкающий. Нетрудно представить себе, как они вращались. Или возьмите, например, точилку для карандаша в правую руку, а левой вращайте грифель. Вы сразу заметите, что и здесь проявлена асимметрия.

Наконец, посмотрите на гитары, скрипки и другие струнные инструменты. Они симметричны (если не принимать во внимание толщину струн и расположение колков). Но вся система из скрипки и смычка асимметрична. Любопытно было бы узнать, существуют ли левщи среди скрипачей!

И у великих людей есть свои проблемы. Весьма важный для общественного деятеля вопрос: куда девать руки? В фильме «Великий диктатор» непревзойденный Чарли Чаплин пытается найти решение этой проблемы, прежде чем показаться народу. Он становится перед зеркалом. Конечно, лучше всего было бы просто сунуть руки в карманы. Но нельзя же ронять свое достоинство! И вот Чаплин перебирает все мыслимые положения. В конце концов он скрещивает руки на груди в позе, по его мнению, наиболее впечатляющей современников.

Рассматривая картины, памятники или парадные портреты, нетрудно заметить, что существует всего несколько эффектных положений рук. Но для нас интерес представляют лишь скрещенные руки. Не поленившись испробовать это, вы обнаружите, что существуют два варианта. Ваша правая рука ложится так, что ее кисть прячется под левым предплечьем. Или наоборот: правая кисть лежит на левом предплечье, а левая прячется под правой рукой.

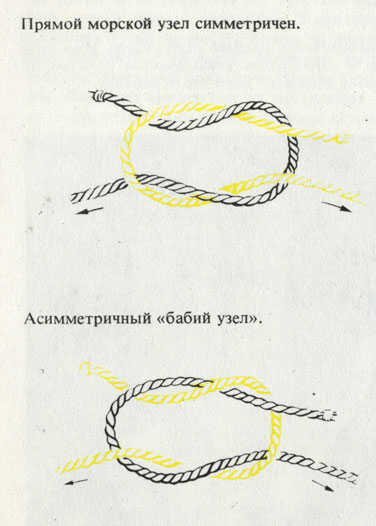
Прямой морской узел симметричен. Асимметричный 'бабий узел'

Представьте себе, что это не руки, а шнурки для ботинок. Их тоже можно перехлестнуть слева направо или справа налево.

На языке моряков такое простое соединение называется «полуштык». Если вам не верится, что вы связали ваши конечности, узлом, попросите, чтобы вам дали по кончику веревки в каждую из перекрещивающихся рук. Теперь выньте руки из подмышек - на веревке окажется узел «полуштык».

К этой «половине» узла следует, естественно, добавить вторую половину, чтобы получился цельный узел. Но если вы попробуете это сделать, будьте внимательны! Здесь существуют два возможных варианта. Если вы «правильно» положите концы веревки, то получите узел «плоский штык». Стоит вам положить их «неправильно», и у вас выйдет «бабий узел», внушающий отвращение всякому моряку. «Бабий узел» затягивается крепко, и развязать его очень трудно. «Плоский штык» также крепко затягивается, но развязать его весьма просто, стоит только подвигать соответствующие концы навстречу друг другу. Для нас же в обоих случаях имеется еще одно существенное различие: «плоский штык» симметричен, а «бабий узел» асимметричен.

Тросы и канаты бывают свиты справа налево (по букве Z) или слева направо (по букве S). При намотке снастей следует обращать внимание на направление, в котором свита веревка, иначе могут возникнуть петли

Но вернемся еще раз к Чарли Чаплину. Обе перекрещенные руки (или концы веревки) по сути дела воспроизводят витки винта и лишены симметрии. Поэтому переплетающиеся концы и невозможно мысленно перевести один в другой. Они соотносятся как изображение и его зеркальное отражение. И если вы завяжете «полуштык» перед зеркалом, ваше отражение в зеркале завяжет его «наоборот». Для того чтобы после второго перехлеста получился правильный морской узел, он должен завязываться зеркально по отношению к первому.

Канаты или тросы могут быть свиты слева направо или справа налево. Бывают канаты (и тросы), скрученные справа налево по букве Z и скрученные слева направо по букве S. Имеется в виду длинный средний элемент буквы, направленный вдоль волокон каната. Расположение этих элементов в буквах зеркально по отношению друг к другу, что в той же мере относится и к соответствующим канатам.

Знают ли эти молодые люди, что они 'завязали' друг перед другом руки левым и правым узлом?

Впрочем, если вы станете разглядывать вашу бельевую веревку, может оказаться, что она вообще не свита, а сплетена. Витые канаты под нагрузкой растягиваются, а сплетенные почти нет. (Бельевая веревка, которая растягивается, когда на нее повесят мокрое белье, не очень-то удобна!) Интересно, кстати, что и улитка завивает свой домик Z-образным витком.

В специальной книге о морских узлах мы находим около 4000 различных задач на завязывание канатов. Многие из этих узлов очень привлекательны на вид, но безнадежно асимметричны.

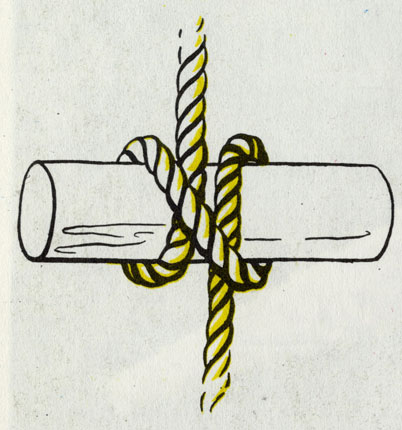
На картинках, изображающих старинные парусные корабли, видно, как матросы карабкаются на мачты по веревочным лестницам. У моряков это называется «взбираться по вантам». Ванты - это длинные канаты или тросы, которые тянутся от бортов корабля к мачте. К ним крепятся веревочные «перекладины». Эти короткие отрезки снастей должны быть прикреплены «намертво» (ни в коем случае не узлом «плоский штык»!). Как выглядит подобное закрепление, показано на рисунке. На первый взгляд оно кажется симметричным, однако это не так. Такое же впечатление производят и всевозможные декоративные узлы. Их можно встретить и в художественных изделиях, и на военном мундире.

Этой большой улитке около 50 млн. лет. Ее витки закручены по букве Z

Морской узел «плоский штык» дает нам еще один прекрасный пример симметрии. Здесь необходимо рассматривать не только симметрию формы, но и симметрию нагрузки. Наш перекрестный узел можно завязать (правильно!) таким образом, что вначале связываются между собой концы каната, которые впоследствии должны испытывать нагрузку. Но можно завязать его и так, что нагруженный конец будет соединен со свободным, ненагруженным («самораспускающийся» узел). В.завязанном виде оба узла практически неразличимы. Однако если нагрузить неверно завязанный узел, то он не станет держать. Как говорят моряки, узел «разъедется».

Именно его и используют в своих представлениях фокусники и иллюзионисты. Раньше, когда на кораблях еще существовали гамаки, всегда находились услужливые помощники крепить новичку его гамак. Естественно, среди ночи доверчивый новичок оказывался на полу.

Математикам и инженерам нередко приходится заниматься узлами и решать связанные с ними задачи. Теоретически интересно знать, какие существуют типы узлов. Но практиков волнует иной вопрос: как создать транспортный узел для беспрепятственного движения потоков автомашин или людей. Такого рода «узлы» можно видеть на топологической схеме наземного и подземного транспорта Берлина.

Существуют даже патенты на узлы. Имеется, например, американский патент, основанный на специальном узле - ленте Мёбиуса. Немецкий математик Август Фердинанд Мёбиус (1790-1868), перекрутив один раз плоскую ленту под углом 180°, склеил оба ее конца. Эта лента обладает удивительным свойством. Если мы, коснувшись пальцем одной из ее сторон (заметим которой), будем скользить им вдоль по поверхности, то обнаружим, что у этой ленты существует только одна поверхность (не перекрученная таким образом лента, естественно, имеет две поверхности). На этом свойстве и основан патент. При использовании приводного ремня (говорится в патентном описании) его внутренняя сторона, пробегающая над ведущим и ведомым колесами, со временем снашивается и становится непригодной. При использовании ленты Мёбиуса по существу исчезает разница между внутренней и внешней поверхностью и износ ремня соответственно намного уменьшается. Собственно, это и было запатентовано.

Саморазвязывающийся узел, которым часто пользуются фокусники. Если потянуть за 'нужный' конец, узел распустится

Если сделать ленту Мёбиуса прозрачной и нанести на нее какой-нибудь значок, скажем букву N, то обнаружится, что противолежащие фигуры соотносятся как изображение и его зеркальное отражение. Это весьма любопытно, учитывая, что «прямая» и «противолежащая» буквы находятся на одной стороне ленты! Ведь у ленты вообще всего одна поверхность.

При конструировании сложных пересечений важно знать одно свойство узлов, которое мы выведем с помощью эксперимента. Нарисуйте любой транспортный узел. Он может быть запутанным и неправильным. Пометьте только каждое пересечение буквой, разумеется, в каждом случае разной. Теперь ведите карандашом или пальцем по вашему рисунку в направлении, обратном тому, в каком вы рисовали. И всякий раз, проходя пересечение, записывайте соответствующую букву. Чтобы результат (который мы стремимся найти) был нагляднее, записывайте буквы в два ряда: либо слева направо, либо сверху вниз. Важно только, чтобы вы чередовали перекрестки (в зависимости от того, проходит улица над или под другой). Причем не играет роли, каким вы приняли первое пересечение - верхним или нижним. Когда табличка будет готова и вы как следует проверите ее, то обнаружите, что каждая буква, обозначающая перекресток, встречается в каждом из рядов по одному разу.

Симметричен ли изображенный здесь морской узел?

Представьте себе, что вы должны спроектировать систему светофоров, регулирующих проезд транспорта. В одном ряду окажутся все светофоры, включенные на зеленый свет, в то время как все светофоры другого ряда должны быть включены на красный.

Фокусники-любители используют знание теории узлов для изящного «эксперимента по чтению мыслей». Вы просите нарисовать подобный узел и обозначить его буквами (не подглядывая), а потом предлагаете объехать препятствие, называя буквы (которые фокусник записывает по известной уже схеме). В каком-нибудь месте два перекрестка «путаются». И фокусник, «читая» мысли, называет встретившиеся буквы. Как легко проверить, перепутавшиеся буквы дважды попадутся в одном ряду.

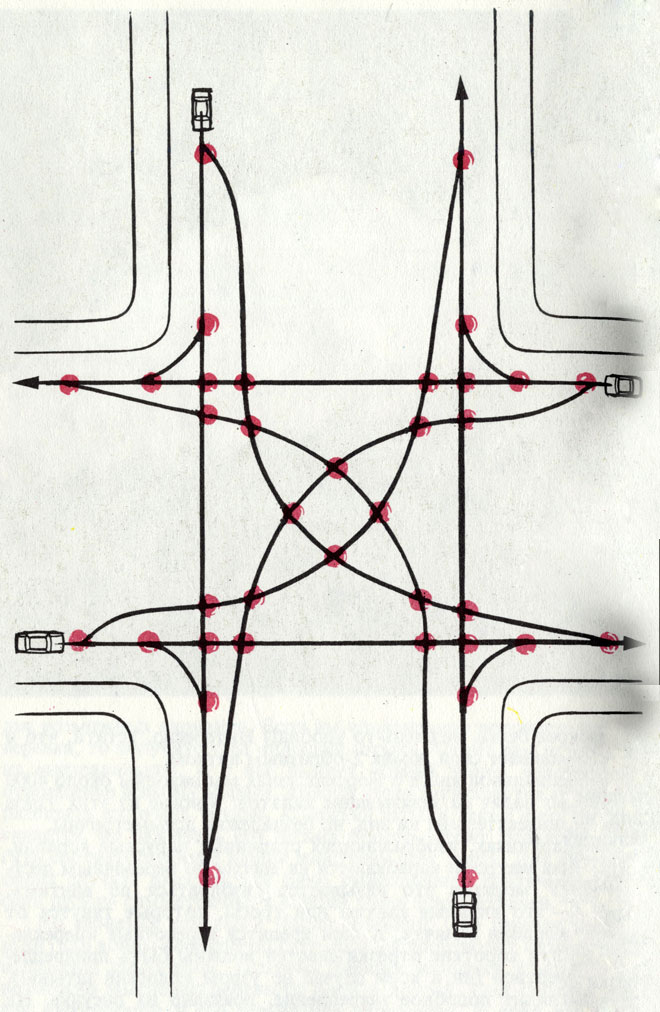
Всякий перекресток - это задача на 'узлы'. На изображенном здесь перекрестке существует 32 возможности столкновения

В заключение этого раздела еще один вопрос: а что произойдет, если ленту Мёбиуса разрезать вдоль? В случае простой, не перевернутой ленты это ясно: получатся две новые ленты, которые будут вдвое уже первой. Что же случится с лентой Мёбиуса, которую мы предварительно перекрутили, прежде чем склеить ее концы, трудно и представить! Если после одного поворота уже «исчезла» одна сторона, то в этом случае можно ждать чего угодно. Сформулируем вопрос несколько иначе: что случится, если владелец запатентованной ременной передачи разрежет ее вдоль, чтобы из экономии получить две ременные передачи? Опыт подсказывает нам, что двух новых лент не получится. Возникнет замкнутая лента, вдвое большей длины. Она, хотя и перевита, но, как всякая нормальная лента, снова имеет две стороны.

Перелистните, пожалуйста, несколько страниц назад и еще раз взгляните на пять Платоновых тел. Только эти пять тел (повторим это еще раз) можно построить из одинаковых правильных плоских фигур - граней.

Тетраэдр нам знаком из повседневной жизни. В пакетах-тетраэдрах мы покупаем молочные продукты. Некоторое время назад дискутировался вопрос, почему для этих целей использует-се именно тетраэдр, а не гексаэдр, то есть куб. Ведь куб имеет наименьшую (после шара) поверхность по отношению к объему. Поэтому при такой упаковке для того же объема молока понадобилось бы меньше упаковочного материала, чем при упаковке в тетраэдры. Однако если мы посмотрим на развертки обоих тел, то увидим, что тетраэдры можно складывать из непрерывной движущейся ленты. А вот кубы из простой ленты не получатся. Два квадратика всегда будут торчать, так что обрезков всегда будет оставаться гораздо больше, чем при склеивании пакетов-тетраэдров.

Основной мотив узора многих футбольных мячей состоит из пятиугольника, окруженного пятью шестиугольниками

Этот небольшой пример позволяет проанализировать часто встречающуюся ошибку. Нередко в поисках оптимального решения мы забываем точно определить, что же именно следует оптимизировать. Нижненемецкая поговорка гласит: «Что подходит сове, то негоже соловью». На современный лад это звучит примерно так: «Если создать оптимальные условия для соловьев, каково придется совам!» (И наоборот!)

В нашей задаче об упаковке можно поставить множество вопросов, в зависимости от того, что же именно должно быть оптимальным:

1. Что дает наименьший расход упаковки при том же объеме содержимого? (Шар, куб.)

2. Какое тело легче всего получить из плоского листа путем простого складывания? (Пять Платоновых тел, то есть не шар!)

3. Какое тело при сборке имеет минимальную по длине соединительную полосу, которую можно склеить, сварить или соединить еще каким-то способом? (Тетраэдр.)

4. При выкройке какого тела получается минимум обрезков? (Тетраэдра.)

5. Какие тела можно сложить наиболее плотно, без просветов? (Куб, тетраэдр.)

6. У какого тела наименьшая вероятность «перепутать» грани в том случае, если оно должно лежать определенной стороной кверху (скажем, чтобы была видна маркировка)? (У тетраэдра, у него меньше всего граней.)

Из постановки этих шести вопросов нетрудно понять, как тщательно следует уточнять, что именно мы собираемся оптимизировать.

Если перед нами встанет задача разработать форму упаковки для грузов, предназначенных для пересылки самолетом, определяющими критериями оптимизации будут пункты 1 (маленький упаковочный формат) и 5 (плотная укладка без зазоров), так как при воздушных перевозках каждый грамм стоит дополнительных денег. Но при выборе тары для перевозки молока главную роль играет пункт 3 (наименьшая длина линии склейки) и даже еще более важную - пункт 4 (минимальные отходы). Сюда добавляются еще преимущества пунктов 5 (плотность укладки) и 6 (наименьшая вероятность уложить пакеты не той стороной).

Если объезжать этот 'узел' по стрелке, то б.уквы появятся один раз в 'непрямом' ряду и один раз - в прямом

Перед футурологами уже сегодня встает проблема: будем ли мы в 2000 г. покупать молоко в тетраэдрах или только в порошке, а может быть, нам снова придется возиться с молочными бидонами?

Однако в этой книге нас прежде всего интересуют вопросы, более близкие теме.

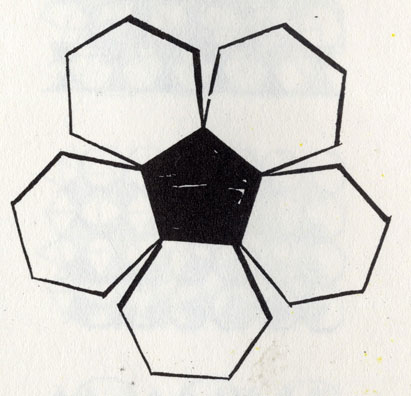
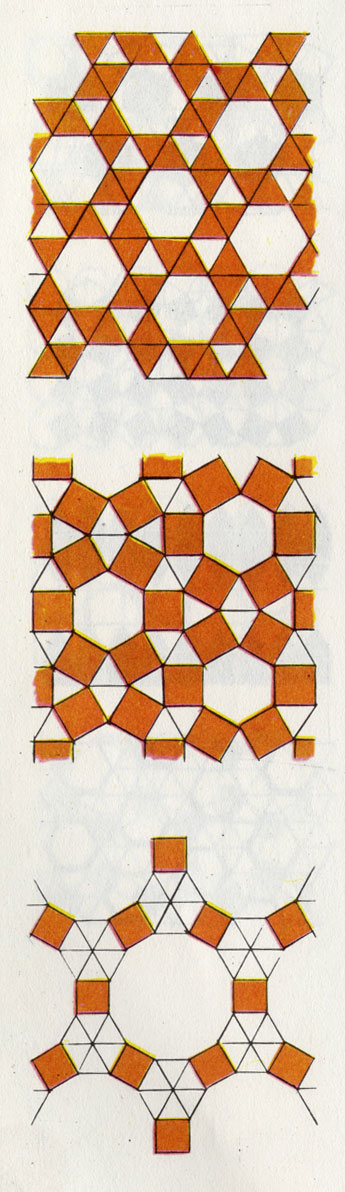
Право же, удивительно, что из пятиугольников тоже можно построить многогранник. А почему это невозможно из шестиугольников? Тем более что шестиугольник можно построить из шести треугольников?

Пятиугольники и шестиугольники нельзя уложить на плоскости без зазоров. Эти зазоры закрываются при образовании шара

Очевидно, дело тут не только в самой исходной плоской фигуре (треугольник, квадрат, пятиугольник), но и в том, как эти поверхности, примыкая, соединяются друг с другом. Если шестиугольники выложить на стол, станет ясно, что они покрывают плоскость без зазоров. Это свойственно также треугольникам и квадратам. А вот сложить из шестиугольников, не деформировав их, объемное тело, невозможно. Если все же попытаться с легким нажимом сделать такой многогранник из шестиугольников, его грани выгнутся и форма будет приближаться к шарообразной.

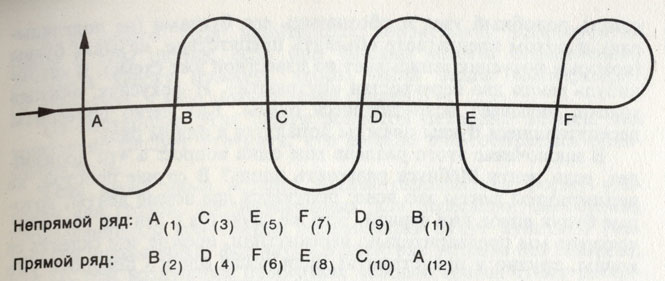
Шаровую конструкцию особого рода представляет собой футбольный мяч. Миллионы людей много раз в неделю видят этот мяч на экране телевизора. Сотни тысяч видят его «в натуре», на стадионе. Все знают, что покрышки мяча состоят из белых и черных фигурок. Но, как ни странно, лишь немногие могут с уверенностью сказать, из каких именно многоугольников он сделан. Даже футболисты колеблются, вспоминая, из пяти- или из шестиугольников. Это типичный пример нашей невнимательности в повседневной жизни.

Используя многоугольники разных видов, можно создать множество узоров для кафельного пола

Прежде кожаная покрышка делалась из двухконечных долек, подобных тем, которые надрезаются на апельсиновой кожуре. У большинства современных мячей покрышка состоит из изогнутых многоугольников. Она весит около 300 г при окружности мяча около 64 см и составляется из 12 черных и 20 белых «полей». Ребро каждого многоугольника независимо от числа его углов имеет в длину 4,3 см. Вокруг каждого черного пятиугольника располагается шесть белых шестиугольников.

Как уже говорилось, на плоскости шестиугольник, окруженный шестью другими шестиугольниками, образует мотив сплошного узора. Пятиугольник, окруженный пятью шестиугольниками, не заполняет всю плоскость без зазоров. Но если с некоторым усилием соединить такие многоугольники из кожи, получится (с весьма хорошим приближением) шар - наш футбольный мяч. Пространственно деформированные шестиугольники применяются и в строительстве при сооружении современных облегченных конструкций.

На рисунке показано 8 полурегулярных мотивов узора, каждый из которых включает два или больше различных типов правильных много угольников, соединенных углами или сторонами. В каждом углу сходится одинаковое число образующих узор многоугольников

Таким образом, из недеформированных плоских фигур одного типа и размера могут быть сложены только пять Платоновых тел.

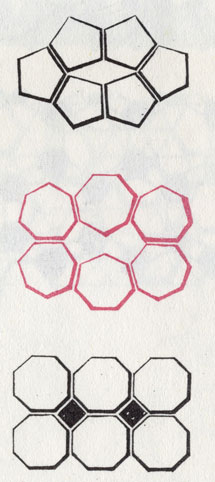
Большие возможности для комбинаций из плоских фигур открываются при составлении узоров из кафельных плиток (например, на полу в ванной комнате). В них бесконечно повторяются мотивы из равносторонних треугольников, квадратов и шестиугольников. А вот с пятиугольными плитками плиточник едва ли смог бы что-нибудь сделать. Их невозможно сложить в подобный узор.

Особые свойства равностороннего или равнобедренного треугольника (ибо квадрат состоит из двух равнобедренных, а шестиугольник из шести равносторонних треугольников) связаны с суммой его углов, которая составляет 180°. Сумма углов всякого n-угольника равна (n - 2) • 180°. У пятиугольника она будет (5-2) • 180° = 540°. Разделив 540 на 5, мы получим для каждого угла 108°. В точках, где сходятся все плитки, сумма всех углов должна составлять 360°. Но из углов, равных 108°, невозможно составить суммарный угол в 360°!

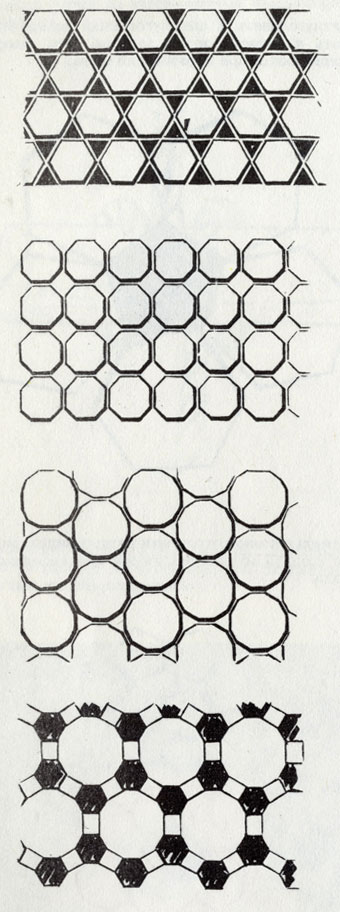
Мы уже говорили, что узор из плиток можно составить только в том случае, если взять правильные треугольники, квадраты и шестиугольники. Однако это справедливо лишь тогда, когда прикладывается сторона к стороне и угол к углу. Но эти три вида многоугольников обнаружат различия, как только мы изберем другой мотив узора для нашего пола. Квадраты и равносторонние треугольники будут заполнять всю плоскость и в том случае, если они не примыкают углом к углу. В мотиве, выложенном шестиугольниками, между примыкающими углами и сторонами образуются зазоры. Но сами эти зазоры способствуют созданию новых восхитительных узоров. Для шестиугольников существуют четыре мотива их сочетания в единый узор с треугольниками и квадратами.

Кроме того, известны еще две комбинации, в которых участвуют только квадраты и треугольники, и две, в которых плюс к тому используются еще и восьми-, и двенадцатиугольники. Созданием «узоров для кафеля» увлекались многие математики.

При выкладывании узоров из кафельных плиток нет границ для фантазии

Так, известно, что Иоганн Кеплер занимался составлением узора из шестиугольников, окруженных треугольниками. Любопытно, что этот узор (и только он) может иметь зеркально симметричное изображение. Остальные узоры в зеркале не меняются. Переворачивается только узор Кеплера.

Взяв любые -многоугольники и не ограничиваясь особыми правилами при их соединении, мы можем придумать великое множество мозаичных узоров. Русский кристаллограф Е. С. Федоров в 1891 г. доказал, что при этом выделяются 17 различных групп симметрии. На практике эти группы были известны уже арабам и использовались ими в мозаиках Альгамбры в Испании.

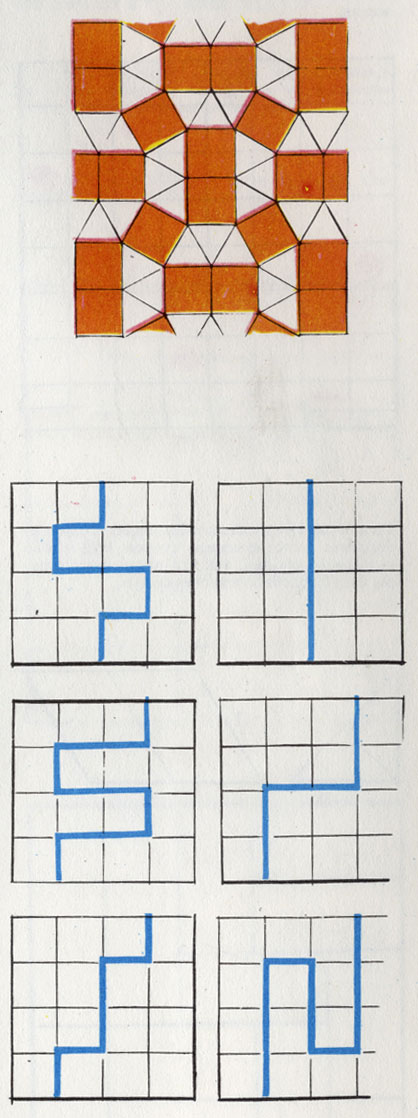
Глаз человека склонен все дальше дробить увиденные узоры, особенно если они контрастны по цвету, как, к примеру, шахматная доска. Начнем с «шахматной доски», состоящей всего из двух рядов по две клетки. (Вместо шахматной доски можно взять четыре квадратные кафельные плитки пола или стены.)

Как можно разделить пополам узор, состоящий из 2X2 плиток? Ответить на этот вопрос, разумеется, не трудно. Только одной чертой, проходящей посередине либо слева направо, либо сверху вниз и отделяющей две клетки (слева или сверху).

Квадрат, составленный из 4Х4 клеток, можно разделить пополам шестью способами

Доску, состоящую из 3Х3 клеток, разделить пополам (не перекая клетки) невозможно. В некоторых играх, правда, используются игровые поля 3Х3, 5Х5 и т. д., исключающие середину я чтобы при делении игрового поля пополам получилось целое число клеток. Но мы здесь не будем рассматривать такие уже и от тех, что складываются из целого числа клеток, голова может пойти кругом.

Сколько существует возможностей разделить пополам узор, составленный из 4 х 4 клеток, не пересекая их? При этом мы пренебрежем различием верх - низ и левое - правое. (Такие решения можно перевести друг в друга простым поворотом.) Тот, кто как следует повозится с таким делением, найдет, худо - бедно, 6 способов.

А если попробовать разделить поле 6x6 клеток? Английский мастер головоломок Генри Э. Дьюдени нашел 255 способов деления такого поля. Для шахматной доски с 64 клетками (8Х8) компьютер рассчитал 92 263 варианта деления!

Существует множество аналогичных задач, над которыми бьются шахматисты и математики. Излюбленными остаются задачи такого рода: сколько ферзей (или слонов, или ладей) можно выставить на одну доску, чтобы они не угрожали друг другу? (Для тех, кто не играет в шахматы, следует заметить, что ферзь имеет право ходить во все стороны, включая и диагонали, сколь угодно далеко.) Любители шахмат определили, что на доске могут находиться 8 ферзей.

Тут встает следующий вопрос: сколько существует вариантов их расстановки? В 1850 г. Франц Наук опубликовал в лейпцигской «Иллюстрированной газете» ответ: таких основных позиций 12.

Поскольку мы много говорили о зеркальных плоскостях, надо надеяться, вы, не задумываясь, проведете плоскость симметрии через шахматную доску сверху вниз. Это будет первым решением.

Следующую плоскость зеркального отражения вы можете провести слева направо, еще две плоскости пройдут по диагонали. Таким образом, мы нашли еще четыре решения. Теперь повернем поле на 180° и снова проведем две диагональные плоскости зеркального отражения и одну - сверху вниз. Но вот провести плоскость симметрии слева направо мы больше не сможем: она даст нам только ту же картину, которую мы уже видели.

Таким образом, путем простого зеркального отражения и вращения мы добавили к основной позиции фигур еще семь вариантов. За одним-единственным исключением, эта операция возможна и для всех остальных основных положений, которые нашел Наук. В упомянутом исключительном случае существует только три отражения. Всего ферзи могут быть одновременно расставлены на шахматной доске, не угрожая друг другу, в 92 различных позициях.

Этот пример учит нас тому, как можно извлечь пользу из наличия симметрии. Разумеется, сначала необходимо было установить, что на иоле могут находиться только 8 ферзей. Потом нужно было выработать 12 основных исходных позиций, что, конечно, было нелегко. Но остальные 80 вариантов можно было найти, отнюдь не будучи специалистом в шахматах. Достаточно было знать, как действует зеркало. С другой стороны, следует признать, что наверняка существует немало выдающихся шахматистов, которые никогда не слыхали о плоскостях симметрии.

Говорят, что всякую проблему можно рассматривать с трех точек зрения: с моей, с твоей и с точки зрения фактов.

Несомненно, что-то в этом афоризме есть. Стакан может быть полупустым или наполовину полным. В кармане может быть целых 5 рублей или всего лишь 5 рублей! Пассажиры переживают сильный шторм, а видавший виды капитан в то же время ощущает лишь свежий бриз.

Определим, что такое шахматная доска. Можно сказать, что это 64 клетки, расположенные в 8 продольных рядов по 8 клеток в каждом, так что в целом все вместе они образуют квадрат. Но можно выразиться иначе: это квадрат, разделенный на 64 равные квадратные клетки. (В обоих случаях надо бы еще сказать о черных и белых полях, но, поскольку для наших целей это обстоятельство несущественно, опустим эту часть определения.) В первом случае мы образуем большой квадрат из маленьких, во втором - делим большой на маленькие.

Один из вариантов расстановки на шахматной доске восьми ферзей, при котором эти фигуры не могут угрожать друг другу. Остальные комбинации получают путем зеркального отражения

Ради любопытства спросим, а на сколько частей можно разделить квадрат так, чтобы возникли маленькие, но одинаковые квадратики? Очевидно, что квадрат делится как минимум на 4 меньших квадрата. На 2 или на 3 квадрата разделить его невозможно. При следующем делении каждый из четырех малых квадратов разделится на 4 еще меньших, то есть всего станет 16 квадратов. Ход деления мы узнали. Результат всякий раз получим умножением на 4. Соответственно при следующем делении 16 квадратов мы получим 64, то есть шахматную доску. Существуют только две плоские фигуры, которые можно разделить на две равные части, причем эти части будут точным уменьшенным воспроизведением больших фигур. Так как мы привыкли делить пополам все, что встречается вокруг, приходится только удивляться тому, что лишь в двух случаях мы можем соблюсти сформулированное выше условие. Это такие фигуры: прямоугольный раЬнобедренный треугольник и параллелограмм с соотношением сторон 1: √ 2.

Такой параллелограмм в одном частном случае - в форме прямоугольника - играет существенную роль в искусстве и технике. Прямоугольник, длинная сторона которого больше его короткой стороны в √ 2 раз (то есть в 1,4142 раза), воспринимается нами как соразмерный. Именно такой или близкий к нему формат картин предпочитают художники.

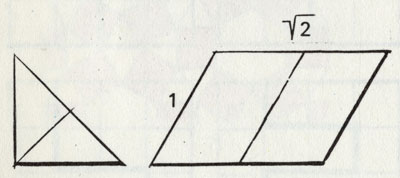
Только равнобедренный треугольник и параллелограмм с соотношением сторон 1:√ 2 можно разделить пополам, так что полученные фигуры будут подобны первоначальным

В фотографии широко распространены форматы 7Х10 (прежде был 6x9) и 13Х18. Если рассчитать соотношение сторон, получается 10:7 ≈ 1,43, а 18:13 ≈ 1,38, то есть числа, близкие к √ 2 = 1,4142.

Более точно придерживаются отношения 1 : √ 2 в технике. На нем основан формат бумаги. Так, при формате АО (841 х 1189 мм) отношение сторон составляет 1,413 ≈ √ 2. Если перегнуть лист пополам, по большей стороне, получится формат А1 (841Х1189/2, то есть 841X594 мм), где 841:594 = 1,415. Дальше снова складывается пополам большая сторона. Получается формат A3. При следующем складывании мы получим известный формат А4, в котором 291:210 = 1,414. Такое деление идет дальше до формата А8 (74:52).

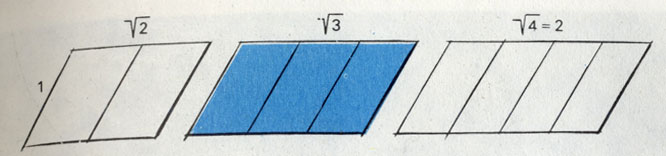
Параллелограммы с соотношением сторон 1 :√ 2, 1 :√ 3 и т. д. можно разделить на две, три и соответственно более частей, так что у новых полученных подобных фигур соотношение сторон сохранится первоначальным

Тот, кто имеет дело с бумагой, знает, что существуют еще два других ряда - для суперобложек и прочих целей. Ряд В начинается с 1414:1000 = 1,414 и ряд С - с 1297:917 = 1,414...

Книга, которую вы читаете (и, хотелось бы надеяться, не без интереса), имеет формат 260Х200 мм, а 260:200 = 1,3.

Конечно, вы обратили внимание, что формат бумаги здесь обозначен не совсем так, как принято: не через произведение сторон, а через их отношение, но мы позволили себе это для большей наглядности.

Мы могли бы сказать, что расчет формата бумаги, отвечающего стандарту, производится путем повторного деления листа с соотношением сторон 1:√ 2, начиная с формата 917Х1297 мм. Но правильнее будет другое определение: стандартный расчет бумаги производится путем пропорционального увеличения листа с соотношением сторон 1:√ 2, последовательно начиная с формата 52Х74 мм. В обоих случаях следовало бы сделать оговорку, что при делении (или умножении) всякий раз берется сторона с относительной длиной √ 2.

В старину подобные трапеции выкладывались по углам наборных полов; каждая составная часть в них подобна целой фигуре

Вспомним, что прямоугольник является лишь частным случаем параллелограмма и что параллелограмм с соотношением сторон 1:√ 2, равно как и прямоугольный равнобедренный треугольник, можно разделить на две уменьшенные копии.

Параллелограмм, одна из сторон которого равняется √ 3, можно разделить на 3 уменьшенные подобные части. В общей форме: параллелограмм с соотношением сторон 1:√ n можно разделить на n одинаковых подобных частей.

Существует еще множество фигур, имеющих самые различные варианты разделения. Мы же рассмотрим еще один мотив, который иногда выкладывали на старинных кафельных полах по углам. Это трапеции, которые зеркальное отражение превращает в цельный мотив узора. Здесь снова возникает «отражение». Значит, в таких узорах допустимы комбинации плоских фигур, которые нельзя путем поворота или вращения совместить друг с другом, то есть «левые» и «правые».

Как уложить бруски или кирпичи, чтобы конструкция не имела сквозных 'швов'

Приведенный здесь рисунок подводит нас к делениям без нарушения сплошности. Если при уменьшении формата бумаги поверхность фигуры пересекал разрыв (складка или черта), то в нашем главном узоре существуют линии, которые не продолжаются, а упираются в другие линии. Иногда особенно желательно полностью избежать деления с разрывами. Скажем, хотелось бы, чтобы стена кирпичного дома не имела шва, пересекающего всю стену сверху донизу. Инструкции по сварке барабанов котлов и нефтяных труб большого диаметра запрещают соприкосновение двух продольных и двух поперечных швов. В каждый поперечный или круговой шов может упираться лишь один продольный шов одного направления. Продольный шов другого направления должен быть непременно смещен в сторону. Благодаря этому разрывы в продольном шве будут распространяться только до следующего поперечного шва.

Теперь вы, наверное, уже догадались, какая предлагается вам задача: соберите из стандартных деталей (кирпичей, паркетин или листов жести) изображенную здесь поверхность, не нарушая ее сплошности.

В старину рудокопы были людьми сугубо практическими. Они не забивали себе голову названиями всевозможных горных пород, которые встречали в штольне, а просто делили эти породы и минералы на полезные и бесполезные, ненужные. Нужные они извлекали из недр, из них плавили медь, свинец, серебро и другие металлы, а ненужные сваливали в отвалы.

Для полезных (на их взгляд) минералов они подыскивали наглядные и запоминающиеся имена. Можно никогда не видеть копьевидного колчедана, но без особого труда представить его себе по названию. Не сложнее по названию отличить красный железняк от бурого железняка.

Для бесполезных камней (как уже было сказано - на их взгляд) горняки нередко находили названия в преданиях и легендах. Так, например, произошло название руды кобальтовый блеск. Кобальтовые руды похожи на серебряные и при добыче иногда принимались за них. Когда из такой руды не удавалось выплавить серебро, считалось, что она заколдована горными духами - кобольдами.

Тяжелый шпат (барит). Рудокопы в стариых выбирали названия для минералов по внешним признакам. Тот, кто однажды взвесил на руке этот минерал и всмотрелся в форму его кристаллов, не забудет его названия

Когда же минералогия превратилась в науку, было открыто великое множество пород и минералов. И при этом все чаще возникали трудности с изобретением для них наименований. Новые минералы часто называли по месту находки (ильменит - в Ильменских горах) или в честь знаменитого человека (гетит - в честь Гете) или же давали ему греческое или латинское название.

Музеи пополнялись грандиозными коллекциями камней, которые становились уже необозримыми. Не слишком помогали и химические анализы, потому что многие вещества одного и того же состава образуют подчас кристаллы совершенно различного облика. Достаточно вспомнить хотя бы снежинки.

Существуют тысячи различных узоров снежинок

В 1850 г. французский физик Огюст Браве (1811-1863) выдвинул геометрический принцип классификации кристаллов, основанный на их внутреннем строении/По мнению Браве, мельчайший, бесконечно повторяющийся мотив узора и есть определяющий, решающий признак для классификации кристаллических веществ. Браве представлял себе в основе кристаллического вещества крошечную элементарную частицу кристалла. Сегодня со школьной скамьи мы знаем, что мир состоит из мельчайших частиц - атомов и молекул. Но Браве оперировал в своих представлениях крошечным «кирпичиком» кристалла и исследовал, каковы могли быть у него углы между ребрами и в каких соотношениях его стороны могли находиться между собой (Для большей наглядности автор упрощает историю вывода решеток Браве. Предшественник Браве - французский кристаллограф Р. Ж. Гаюи (1743-1822) - действительно представлял себе кристаллы сложенными из элементарных «кирпичиков». О. Браве заменил эти «кирпичики» центрами их тяжести и таким образом перешел от «кирпичной кладки» Гаюи к пространственной решетке. - Прим. ред).

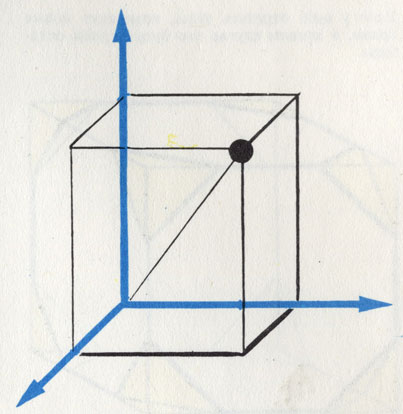
Каждый кристалл можно поместить в систему координатных осей

В кубе три ребра расположены всегда под углом 90° друг к другу. Все стороны имеют равную длину. У кирпича углы тоже составляют 90°. Но его стороны различной длины. У снежинок, наоборот, мы не найдем угла 90°, а только 60 или 120°.

Составленный из квадратов ряд можно разделить диагоналями на ряд других квадратов

Браве установил, что существуют 7 комбинаций ячеек с одинаковыми или разными сторонами (осями) и углами. Для углов он принял только два варианта: равный 90° и не равный 90°. Только один угол во всей его системе в порядке исключения имеет 120°. В самом скверном случае все три оси и все углы ячейки различны по величине, при этом в ней нет углов ни в 90, ни в 120°. Все в ней косо и криво, и, можно подумать, в мире кристаллов таким не должно быть места. Между тем к ним относится, например, сульфат меди (медный купорос), голубые кристаллы которого обычно всем так нравятся.

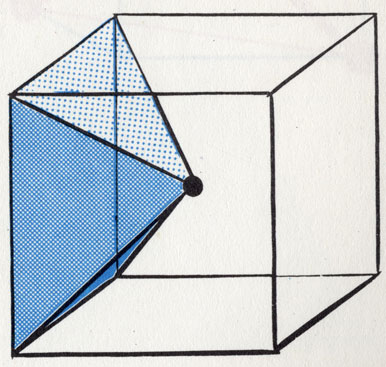
Куб содержит 6 пирамид (для большей наглядности изображена только одна). На каждой из шести квадратных граней можно построить аналогичные пирамиды

В некоторых из этих 7 пространственных решеток элементарные «кирпичики» можно упаковать по-разному. Для нас, знающих сегодня о строении атома, это нетрудно представить и продемонстрировать с помощью шариков для пинг-понга. Но 125 лет назад гениальная идея Браве была новаторской и открывала новые пути в науке Весьма вероятно, что и Браве исходил из узоров кафеля или мотивов шахматной доски.

Если мы разделим квадратные поля диагоналями, то возникает новый рисунок из квадратов, стоящих на углах. В трехмерном Кпостранстве это соответствует кубу, разложенному на шесть пирамид. Каждая такая пирамида составляет половину октаэдра.

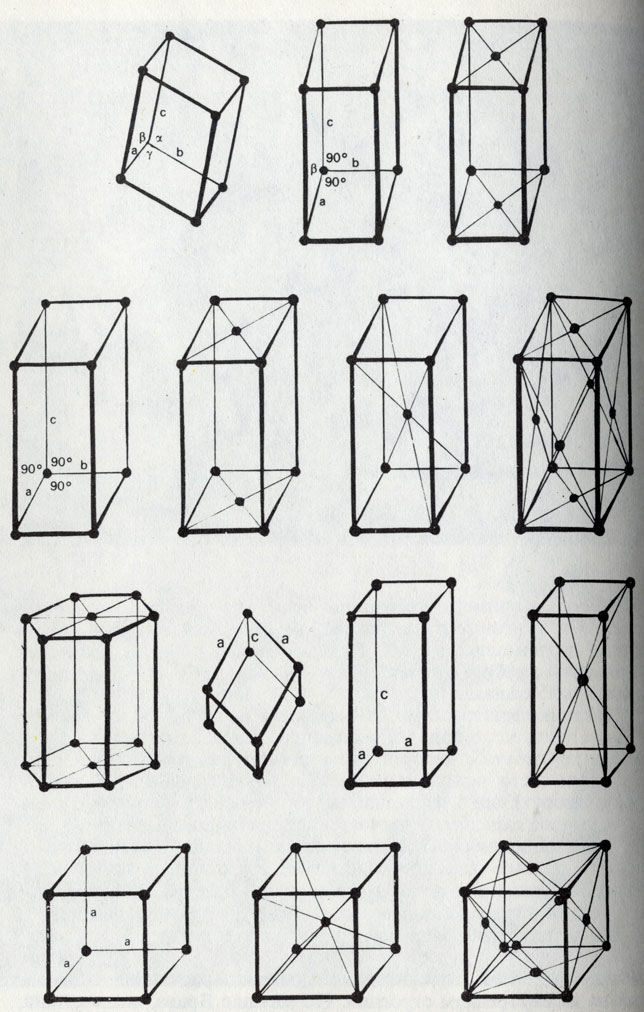
Четырнадцать решеток Браве. Они строятся в семи возможных сингониях (осевых системах). Но при этом во внимание принимается также еще и расположение атомов. Так, кубы нижнего ряда соответствуют одной и той же кубической ячейке

Те кто когда-нибудь выращивал кристаллы поваренной соли, нают, что соль может кристаллизоваться в кубах, а может - в октаэдрах. Иными словами, экспериментальные наблюдения совладают с теоретическими соображениями.

Испробовав возможные варианты упаковки для всех семи осевых систем, Браве вывел 14 решеток. Мы приводим их здесь в нашем современном атомистическом изображении.

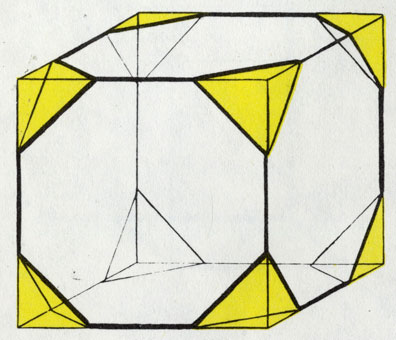
Если у куба отрезать углы, возникнут новые грани, в данном случае это будут грани октаэдра

Рассматривая решетки Браве внимательней и пробуя мысленно построить из них кристаллы, вы, вероятно, увидите, как можно провести в них плоскости и оси симметрии. Эти возможности сразу расширятся, если мы в одной из элементарных ячеек образуем новые грани. Возьмем куб (естественно, мысленно!), поставим его на угол и обрежем (все так же мысленно) все углы, тогда у него образуются совершенно новые треугольные грани. А из квадратных граней возникнут восьмиугольники: тем самым появятся новые мотивы симметрии.

Анализ элементов симметрии в каждой из осевых систем кристаллических решеток приводит к возникновению 32 классов симметрии. Все многообразие минералов в природе подразделяется на основе 32 классов симметрии. Вооруженные этими знаниями, задумаемся о классификации пяти тел Платона. То, что куб, с его тремя равными осями и тремя прямыми углами, относится к кубической осевой системе (сингонии), не нуждается в доказательстве. В рамках более детального подразделения он принадлежит пентагон-тетраэдрическому классу симметрии (К кубической системе относятся 5 из 32 классов кристаллографической симметрии. К ним принадлежат 5 разновидностей куба, различающихся по симметрии. Наиболее симметричный куб имеет 9 плоскостей симметрии, 3 четверные, 4 тройные и 6 двойных осей симметрии.Наименее симметричный куб, о котором и идет речь в тексте, обладает лишь тремя двойными и четырьмя тройными осями симметрии. - Прим. ред). Мы не станем здесь приводить названий других классов из-за их сложности. Однако обратите внимание на термин «тетраэдрический», так как тетраэдр - одно из Платоновых тел.

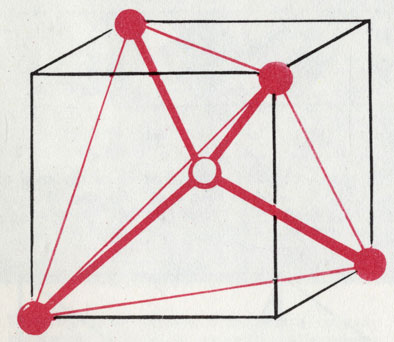
В каждом кубе можно расположить пару тетраэдров

А если у вас хорошая память, вы вспомните и пентагондоде-каэдр, также входящий в этот класс симметрии. На картинке хорошо видно, как тетраэдр можно образовать из куба. Остальные Платоновы тела также относятся к кубической системе. Древние греки, надо думать, ужасно расстроились бы, знай они, что такой прозаический минерал, как серный колчедан, имеет ту же симметрию, что и их «совершенные» тела.