
От качества н количеству
Что же такое интервал? Каков его физический смысл?
Это - пространственно-временной промежуток между событиями, выражающий, говоря словами Минковского, "некий род единства" пространства и времени. Галина лента не имеет абсолютной длины, не имеет абсолютной длительности ("времени жизни" в размотанном состоянии). Но она имеет интервал - "некое единство" длины и длительности.
Причем каждый наблюдатель, измеривший длину и время бытия развернутой ленты своими линейкой и часами, может быть уверен: вычисленная величина квадрата интервала ленты и у него, и у всех его коллег из других иначе движущихся систем отсчета получится точно такой же.
В этой неизменности (физики говорят - инвариантности) интервала - драгоценное свойство природы, рецепт для вычисления количественных релятивистских эффектов. Прежде нам были доступны лишь смутные, чисто качественные рассуждения. Я произносил неопределенные слова "длиннее", "короче", "быстрее", "медленнее", и только. Теперь же открыта дверь к математической точности, к числу.
Благодаря инвариантности интервала я вправе сделать о ленте следующее математическое утверждение, объединяющее точки зрения и Гали и Вали:
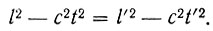
А из этого равенства после не очень сложных выкладок вытекают знаменитые формулы, называемые преобразованиями Лоренца*. Привожу их, по традиции этой книжки, без вывода. Для двух систем отсчета, равномерно движущихся друг относительно друга по прямым параллельным путям, релятивистские длительности явлений и продольные релятивистские длины даются выражениями:
* (По имени известного физика, который сумел вывести их за год до Эйнштейна, исходя из совсем других, неверных представлений: Лоренц думал, что движущиеся тела сплющиваются эфирным ветром.)
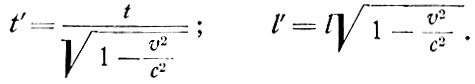
Здесь t' - релятивистская длительность, t - собственная длительность, l' - релятивистская длина, l - собственная длина, с - скорость света, v - относительная скорость систем отсчета.
Формулы просты и красноречивы. Сразу видно, при каких условиях они начинают удивлять: когда относительная скорость вплотную приближается к скорости света. В противном случае, для малых скоростей, с практически беспредельной точностью действуют старинные правила Галилея:
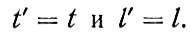
|
ПОИСК:
|