
Трение
Полезно или вредно трение? Многие, не задумываясь, отвечают: "Конечно, вредно!" Но ведь, если бы не было трения, мы не могли бы ходить по земле (вспомните, как скользят ноги на льду), нельзя было бы ездить на велосипеде, автомобиле, мотоцикле (колеса вертелись бы на месте), нам нечего было бы носить (нитки в ткани держатся силами трения). Если не было бы трения, вся мебель в комнате сбилась бы в один угол, тарелки, стаканы и блюдца соскальзывали бы со стола, гвозди и шурупы не держались бы в стене, ни одной вещи нельзя было бы удержать в руках и т. д. и т. п. К этому можно добавить, что, если бы не было трения, неизвестно, как пошло бы развитие цивилизации на Земле - ведь наши предки добывали огонь трением.
Перечень подобных "ужасов" можно продолжать до бесконечности, но и так ясно, что трение - явление отнюдь не вредное. Оно вредно только в машинах, и инженеры борются там с ним, применяя шарикоподшипники, смазку и т. п.
Что же такое трение?
При перемещении одного тела по поверхности другого всегда возникает сила, препятствующая движению. Она-то и называется силой трения.
Трение - следствие многих причин, но основными из них являются две. Во-первых, поверхности тел всегда неровны, и зазубрины одной поверхности цепляются за шероховатости другой. Это так называемое геометрическое трение. (Даже самые гладкие на глаз поверхности оказываются под микроскопом шероховатыми, с впадинами и выступами.) Во-вторых, трущиеся тела очень близко соприкасаются друг с другом, и на их движении сказывается взаимодействие молекул (молекулярное трение). Поэтому формулу для силы трения можно написать так: F=αN+βS.
В этой формуле α и β - постоянные коэффициенты, N - сила нормального давления, a S - площадь контакта трущихся тел. Так как площадь контакта не очень мала, деформации соприкасающихся тел ничтожны.
Приведенная формула сложна, и поэтому инженеры в своих расчетах пользуются более простой формулой: F=kN. Она читается так: сила трения пропорциональна силе нормального давления. Коэффициент пропорциональности к называется коэффициентом трения.
Формулу F=kN можно вывести следующим образом. Пусть есть пластическое тело, т. е. такое, которое растекается под действием собственного веса, какт например, вар. Для такого тела площадь контакта прямо пропорциональна силе нормального давления: S=γN. Поэтому для пластических тел первоначально написанную формулу силы трения можно переписать так: F=αN+βS=αN+βγN=(α+βγ)=kN. Следовательно, формула F=kN справедлива для пластических тел. Но ее обычно применяют для любых тел, так как степень отражения ею реальной действительности весьма высокая.
Закон F=kN становится неверным тогда, когда сила нормального давления или скорость движения велики. В этом случае выделяется слишком много тепла, что сказывается на трении.
Можно проверить на опыте, что сила трения зависит только от качества трущихся поверхностей и силы нормального давления, а от площади соприкосновения не зависит. Если положить деревянный брусок на линейку (или книгу) сначала плашмя, а затем ребром (узкой стороной) и поднимать один конец линейки, то брусок начинает скользить вниз всегда при одном и том же значении угла а (рис. 3). Это говорит о том, что сила трения не зависит от площади контакта поверхностей.
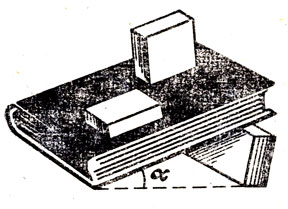
Рис. 3
Вместо бруска можно взять спичечный коробок, в который для тяжести насыпан песок. Только спичечный коробок надо вначале обязательно обклеить бумагой, чтобы все стороны коробка были одинаковы в смысле трения.
Коэффициент трения определяют так. Замеряют динамометром силу, необходимую для перемещения одного тела по поверхности другого, и делят полученное значение силы на вес тела. Найденные коэффициенты вносятся в справочники по физике. Если вам для решения той или иной практической задачи понадобится величина коэффициента трения, ее можно взять из таблицы. Нужно только помнить, что приведенные там значения коэффициентов трения приблизительные. Ведь трущиеся поверхности, как правило, загрязнены. На них бывает ржавчина, окислы и другие посторонние включения, что, естественно, влияет на величину трения. Так как степень загрязнения поверхностей при опытном определении коэффициента трения точно неизвестна, то, строго говоря, нам неизвестно, что же за коэффициент трения мы получили. Скажем, указанный в справочнике коэффициент трения меди по меди на самом деле не коэффициент трения между двумя медными поверхностями, а коэффициент трения между какими-то загрязнениями, имеющимися на меди.
Получить значение коэффициента трения для абсолютно чистых поверхностей невозможно. Допустим, мы вычистили и отполировали два медных бруска, удалили с них жир, дегазировали в вакууме и т. д. Если теперь сложить два куска меди вместе, то они слипнутся и образуют один кусок металла - ведь атомы на границе раздела, образно говоря, не могут знать, какому бруску они принадлежат.
Это явление можно проиллюстрировать следующим опытом.
Привяжите к ножке бокала нитку и поставьте его на стол, накрытый стеклом. Если потянуть за нитку, бокал легко заскользит по стеклу. Теперь смочите стекло водой. Перемещать бокал станет значительно труднее. Если вы присмотритесь к стеклу, то заметите даже царапины. Дело в том, что вода удалила жир и прочие вещества, загрязнявшие трущиеся поверхности. Образовался чистый контакт стекло - стекло. Он настолько хорош, что вырвать кусочки стекла (сделать царапины) оказывается легче, чем нарушить контакт.
Пусть на негладкой поверхности лежит некоторое тело (рис. 4). Его сила тяжести Р уравновешивается нормальной реакцией N. Мы прикладываем небольшую силу Q1, но тело не движется. Это значит, что его держит сила трения Fu которая равна силе Q1. Увеличим немного силу Q1 до величины Q2. Тело продолжает оставаться в покое. Это говорит о том, что его не пускает сила трения F2, равная Q2. И так далее. Но силу Q можно увеличивать беспредельно, а сила трения не может быть больше своего максимально возможного значения F=kN. Когда Q становится равной максимальной силе трения, то этот момент называется порогом покоя или порогом срыва. В следующее мгновение начинается движение.
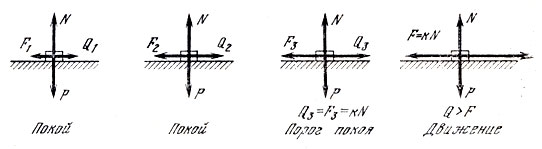
Рис. 4
Следовательно, сила трения изменяется от нуля до некоторого максимального значения, равного kN. Когда нет тянущей силы, нет и силы трения. При наличии движущей силы появляется сила трения.
Несколько слов о конусе трения.
Пусть тело веса Р движется под действием силы Т по шероховатой поверхности (рис. 5). С одной стороны, поверхность не позволяет телу падать вниз под действием силы тяжести Р. С другой стороны, поверхность мешает свободному перемещению тела под действием силы Т. Таким образом, сила трения F так же, как и нормальная реакция, вызвана к жизни поверхностью, т. е. сила трения - это тоже реакция. Нормальная реакция и сила трения складываются в полную реакцию R, которая отклонена от нормали на угол φ. Этот угол называется углом трения. С помощью рис. 5 легко вычислить, чему равен тангенс угла трения
tgφ=F/N=kN/N=k,
т. е. тангенс угла трения численно равен коэффициенту трения.
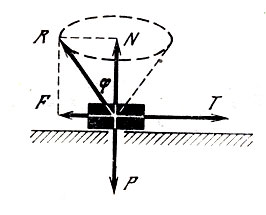
Рис. 5
Теперь представьте себе, что вы вращаете полную реакцию вокруг нормали к поверхности. В этом случае сила R описывает конус, который называется конусом трения. Он интересен тем, что область, ограниченная конусом трения, определяет область равновесия для тела: если сила действует на тело внутри конуса трения, она не сдвинет тело, как бы велика ни была; если сила действует на тело вне конуса трения, она сдвигает тело, как бы мала ни была.
Давайте посмотрим, почему так происходит.
Если сила Q действует внутри конуса трения, то сдвигающая сила Q1=Qsinα (рис. 6). Вычислим силу трения: F=kN=kQcosα=Qcosαtgφ. Запас прочности F-Q1=Q(cosα tgφ-sin α)=Qsin(φ-α)/cosφ. Таким образом, запас прочности пропорционален Q, так как sin(φ-α)/cosφ - постоянная величина. Чем больше сила Q, тем больше удерживающая сила F-Q1.
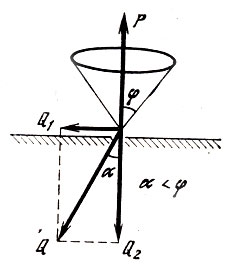
Рис. 6
Конус трения построить очень просто. Пусть, например, нам надо построить конус трения для стального стержня, опирающегося на чугунную плиту. Смотрим в справочник и находим коэффициент трения для стали по чугуну. Ои равен 0,16. Следовательно, надо построить конус, в котором образующая была бы наклонена к нормали под углом 9°, так как тангенс 9° примерно равен 0,16 (sin 9°=0,1584). Понятно, что чем больше коэффициент трения, тем больше угол в конусе трения и наоборот.
Уметь строить конус трения нужно вот почему.
Однажды в Мюнхене рухнул мост, и виноват в этом был не ураганный ветер, не полк идущих в ногу солдат, а... конус трения.
Этот мост одним своим концом был закреплен при помощи шарнира, а другим - положен на катки. Мост всегда крепят таким образом, чтобы он не покривился при колебаниях температуры. Шарнир был заполнен пастой, предохранявшей его от коррозии. В жаркий летний день паста растопилась, и вязкость ее стала меньше. Характер трения изменился - оно также уменьшилось. Конус трения сузился, и сила давления на опору вышла за пределы конуса (рис. 7). Равновесие нарушилось, и мост рухнул.
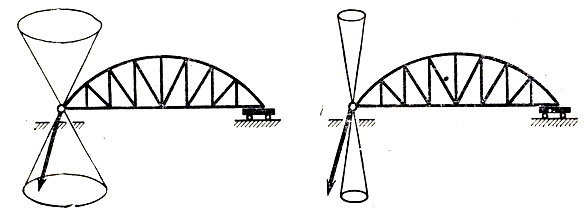
Рис.7
Инженерам часто приходится строить конус трения, чтобы определить, будет ли находиться в равновесии данная конструкция или нет. Но с конусом трения имеют дело не одни только инженеры. Каждый из нас ежедневно сталкивается с этим физическим явлением.
Чтобы пробраться к выходу в переполненном автобусе или троллейбусе, приходится извиваться ужом. Делаем мы это бессознательно, не задумываясь, что таким образом мы выходим из конусов трения в местах касания с другими пассажирами.
Катаемся ли мы на коньках, идем ли на работу, переворачиваем ли страницу в книге - всюду мы сталкиваемся с трением и, в частности, с конусом трения.
Рассмотрим еще один практический пример, связанный с трением. Под каким углом выгоднее всего тянуть веревку, чтобы перемещать тяжелый груз Р по горизонтальной плоскости?
Спроектируем все силы, действующие на груз Р (рис. 8), на горизонтальное и вертикальное направления. Получим два уравнения: Q cosα-kN=0 и Qsinα+N-Р=0, из которых найдем силу Q:Q=P sinφ/cos(α-φ). Мы видим, что Q минимальна, если а = ф, т. е. выгоднее всего тянуть под углом, равным углу трения. Чем плоскость более гладкая, тем более длинную веревку надо брать.
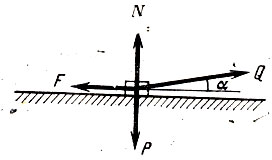
Рис. 8
Теперь поговорим о формуле Эйлера.
Видели ли вы, как сдерживают ход корабля, подошедшего к пристани? С парохода на пристань бросают канат, на конце которого сделана широкая петля. Человек, стоящий на пристани, надевает петлю на причальную тумбу, а матрос на корабле быстро укладывает канат между кнехтами - так называются небольшие тумбы, укрепленные на борту судна. Сила трения между канатами и кнехтами останавливает движение судна.
Неужели сила трения в этом случае так велика? Представьте себе, что вы поднимаете из шахты груз при помощи веревки, переброшенной через неподвижный блок (рис. 9). Если бы трение отсутствовало, то, поднимая груз, пришлось бы прикладывать силу, в точности равную весу груза. Но так как между веревкой и блоком существует трение, то, чтобы поднять груз Р, придется приложить силу Т>Р. Сила T, необходимая для поднятия груза Р, вычисляется по формуле Эйлера: T=Pkφ. Здесь е - основание натуральных логарифмов, k - коэффициент трения, а φ - угол охвата блока веревкой, выраженной в радианах.
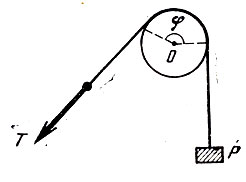
Рис. 9
Давайте подсчитаем, какую силу надо приложить, чтобы удержать корабль у пристани. Пусть движущийся корабль тянет канат с силой в 10 тони. Коэффициент трения каната о железную тумбу известен. Он равен 0,35. Предположим, что матрос обернул канат вокруг тумбы три раза. Тогда угол охвата тумбы канатом ф = 6я. Подставив значения Т, к и ф в формулу Эйлера, получим уравнение 10 000=P•2,726π•0,35, из которого найдем силу Р. Она равняется примерно 15 кг. Следовательно, чтобы сдержать бег судна, матрос должен удерживать канат всего с силой в 15 кг. Обычно матрос, обернув канат несколько раз вокруг кнехтов, просто придерживает свободный конец каната ногой, прижимая его к палубе.
Итак, если корабль тянет с силой в 10 тонн, матросу достаточно приложить силу в 15 кг, чтобы остановить движущееся судно (при условии, что канат три раза обернут вокруг тумбы). Остальные 9985 кг гасятся силой трения.
Приведенный расчет показывает, что при швартовке развиваются довольно-таки значительные силы трения. Раньше, когда причальные тумбы делались из дерева, они, нагреваясь, иногда даже начинали дымиться. В очерке Д. Н. Мамина-Сибиряка "Бойцы" (о сплаве на реке Чусовой) говорится, что по этой причине сплавщики называли причальные тумбы огнивами. Чтобы во время швартовки огнива не загорались, их обливали холодной водой.
В романе Жюля Верна "Матиас Шандор" выведен силач Матифу. Он совершает много подвигов, среди которых есть такой.
Готовился спуск на воду трабаколо - небольшого судна с двумя мачтами и двумя парусами трапециевидной формы. Плотники начали выбивать из-под киля судна клинья, удерживавшие трабаколо на спусковой дорожке. В этот момент в гавань влетела нарядная яхта. Плотники прекратили свою работу, чтобы дать возможность яхте без помех пройти мимо места спуска трабаколо. Но вдруг трабаколо заскользило по спусковой дорожке в воду. Оно неминуемо должно было врезаться в борт плывущей мимо верфи яхты.
"Вдруг из толпы зрителей выскакивает какой-то человек. Он хватает трос, висящий на носу трабаколо. Но тщетно старается он, упираясь в землю ногами, удержать трос в руках. Его не страшит мысль, что трабаколо может увлечь его за собою. Поблизости врыта в землю швартовая пушка. В мгновение ока неизвестный набрасывает на нее трос, который начинает медленно разматываться, а храбрец, рискуя попасть под него и быть раздавленным, сдерживает его со сверхчеловеческой силой. Это длится секунд десять.
Наконец трос лопнул. Но этих десяти секунд оказалось достаточно. Трабаколо... прошло за кормой яхты на расстоянии не более фута...
Яхта была спасена.
А неизвестный, которому никто не успел помочь, - до того неожиданным оказался его поступок, - был не кто иной, как Матифу" (Ж. Верн. Собр. соч. в 12 томах, т. 12. М., 1957, стр. 147).
Жюль Берн, видимо, не был знаком с формулой Эйлера. Иначе он понял бы, что эпизод с трабаколо не может свидетельствовать о силе Матифу. Ведь если канат был обернут несколько раз вокруг швартовой пушки, то удержать трабаколо мог даже ребенок.
Каждый из нас по крайней мере раз в день пользуется формулой Эйлера. Происходит это тогда, когда мы завязываем шнурки на ботинках. Ведь что такое узел, как не веревка, обвитая вокруг другой части той же веревки? И крепость узла тем больше, чем больше изгибов делает шнурок в узле.
В заключение лекции несколько слов о трении качения. Так называется сопротивление, которое испытывает катящееся колесо. Трение качения обусловлено тем, что колесу приходится все время взбираться на небольшой бугорок, образующийся перед движущимся колесом (рис. 10). Чем дорога тверже, тем сопротивление качению меньше. Поэтому автомобильные и мотоциклетные заезды на побитие рекордов скорости проводят обычно по дну высохших соленых озер, которые обладают очень твердой поверхностью.
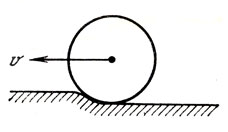
Рис. 10
В гонках участвует далеко не каждый, а вот ездить на автомобиле, мотоцикле, велосипеде приходится очень многим. Как лучше тормозить, если перед вами возникает препятствие?
На поставленный вопрос отвечает вот такой график (рис. 11). Если вы тормозите скольжением, намертво зажимая колеса (так называемый юз), то тормозной путь будет длиннее, чем при торможении качением (колеса заторможены, но проворачиваются), зато скорость вначале падает более резко. Поэтому при опасности наезда надо всегда тормозить юзом. Лучше ударить с меньшей скоростью, так как энергия удара пропорциональна квадрату скорости. Во всех остальных случаях надо тормозить качением: и тормозной путь будет короче, и шины меньше изнашиваются.
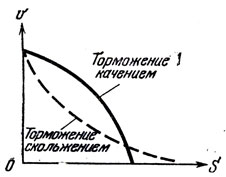
Рис. 11
|
ПОИСК:
|