Меры движения

Чем мерить механическое движение? Этот вопрос волновал многих ученых. Над ним думали Галилей, Декарт, Лейбниц, Гюйгенс, Кант, д'Аламбер и многие другие. Это не такой простой вопрос. Доказательством может служить тот факт, что спор между последователями Декарта - картезианцами - и Лейбницем о мерах движения продолжался более 40 лет.

Декарт предлагал мерить движение произведением массы движущегося тела на его скорость: mv. Лейбниц первым заметил, что Декартова мера движения противоречит закону падения. Поэтому он предложил разделить движущие силы на "мертвые" и "живые". К первым Лейбниц относил "давления" или "тягу" покоящихся тел. За меру их движения он принимал произведение массы m на скорость v, c которой тело двигалось бы, если бы оно перешло из состояния покоя в состояние движения; за меру же живой силы - действительного движения тела - он принимал произведение массы на квадрат скорости, mv² - мера движения, введенная Лейбницем.

Очень хорошо о мерах движения сказано у Ф. Энгельса в его "Диалектике природы". Там есть специальная глава, посвященная мерам движения. Разобрав вначале несколько примеров механического движения тел, Ф. Энгельс заключает: "Таким образом, мы находим, что механическое движение действительно обладает двоякой мерой, но убеждаемся также, что каждая из этих мер имеет силу для весьма определенного ограниченного круга явлений. Если имеющееся уже налицо механическое движение переносится таким образом, что она сохраняется в качестве механического движения, то оно передается согласно формуле о произведении массы на скорость. Если же оно передается таким образом, что оно исчезает в качестве механического движения, воскресая снова в форме потенциальной энергии, теплоты, электричества и т. д., если, одним словом, оно превращается в какую-нибудь другую форму движения, то количество этой новой формы движения пропорционально произведению первоначально двигающейся массы на квадрат скорости. Одним словом: mv - это механическое движение, измеряемое механическим же движением; mv²/2 - это механическое движение, измеряемое его способностью превращаться в определенное количество другой формы движения. И мы видели, что обе эти меры тем не менее не противоречат друг другу, так как они различного характера" (К. Маркс и Ф. Энгельс. Сочинения, т. 20, стр. 418).

Итак, движение материального тела (или точки) можно мерить двояким образом: количеством движения - произведением массы тела на его скорость (mv) и кинетической энергией - полупроизведением массы тела на квадрат его скорости (mv²/2). Первая мера движения векторная (в результате произведения скалярной величины - массы на векторную- скорость получается векторная величина), вторая мера движения скалярная (квадрат вектора скорости, т. е. произведение вектора самого на себя есть скалярная величина).

Аналогично двум мерам движения существуют две меры действия сил. Действие силы на тело (или точку) можно измерять или импульсом силы или работой. Импульс - векторная мера действия силы, работа - скалярная.

В динамике точки (а следовательно, и в динамике поступательного движения твердого тела) есть две важные теоремы. Это - теорема об изменении количества движения

mv-mv₀=∫Fdt,

которая гласит: "Изменение количества движения материального тела за некоторый промежуток времени равняется импульсу всех сил, действующих на тело за тот же промежуток времени", и теорема об изменении кинетической энергии:

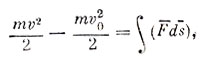
которая читается так: "Изменение кинетической энергии тела на некотором участке пути равняется работе всех сил, действующих на тело, на том же участке пути". Рассказывая об этих теоремах, надо все время подчеркивать, что они не формальные математические записи, а физические законы, устанавливающие соотношения между мерами механического движения и мерами действия сил.

http://eksno.ru/ люк ревизии.