Принцип д'Аламбера

Принцип д'Аламбера формально легко вывести из второго закона Ньютона: ma=F, F-ma-0, F+(-ma)=0. Это и есть принцип д'Аламбера для свободной материальной точки. Для несвободной точки добавляется еще реакция: F+N+(-mа)=0. То, что стоит в скобках, сила инерции.

Можно дать несколько формулировок принципа д'Аламбера.

"Во все время движения сумма всех сил, действующих на материальную точку, включая силу инерции, равна нулю".

"Силы, действующие на материальную точку, и сила инерции всегда взаимно уравновешиваются".

"Если к движущейся под действием сил материальной точке приложить еще силу инерции, то дальше точка будет двигаться равномерно и прямолинейно".

Все эти различные формулировки принципа д'Аламбера выражают одну и ту же мысль: добавление силы инерции к силам, действующим на движущую точку, дает взаимно уравновешивающуюся систему сил, т. е. такое добавление превращает любую динамическую задачу в статическую, и для решения ее можно применять или три уравнения равновесия (для плоской системы сил) или шесть уравнений равновесия (для пространственной задачи). Ценность принципа д'Аламбера и состоит в том, что с его помощью динамические задачи можно решать статическими методами.

Если вы с самого начала привили своим слушателям мысль о дуальности силы, то им очень легко будет понять принцип д'Аламбера.

Силы всегда выступают взаимно уравновешивающимися "двойками". Есть сила F, действующая на материальную точку, и есть сила инерции (-mа), которая приложена к какому-то другому телу. Если теперь взять эту силу инерции и приложить к движущейся точке, то получится, что на точку действует взаимно уравновешивающаяся система сил (рис. 25).

Рис. 25

Сила инерции движущейся точки приложена к двигателю. Это надо внушить.

Обязательно подчеркните, что, пока вы пишете уравнение Ньютона, силы приложены к разным телам. А когда перенесли силу с двигателя на точку, то уже нельзя считать силы, приложенными к разным телам. Теперь - равновесие за счет того, что обе силы находятся на одном теле.

Приведите пример. Магнит притягивает шарик (рис. 26). Все происходит в горизонтальной плоскости на гладком стекле. В основу кладется основной закон противодействия F₁+F₂=0.

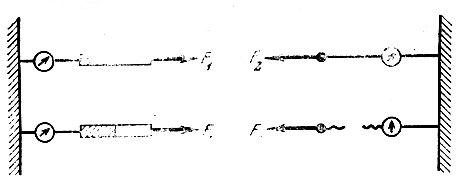
Рис. 26

Дальше самое трудное и страшное. Нить перерезают. Шарик движется, чтобы прилипнуть к магниту. Динамометр на магните показывает прежнюю цифру. Это центральный факт. Все мучались над этим. Значит, на шарик действует то же самое? Что такое F₁? Сила F₁ приложена к движущему телу, а не к шарику, т. е. сила инерции движущейся точки приложена к двигателю.

Другой пример. Два человека стоят на тележках. Первый перебирает веревку и подтягивает к себе второго. Что чувствует при этом первый человек? Материальность второго ощущается не им самим, а тем, кто его тащит.

Когда рассказывать принцип д'Аламбера? По-моему, это надо делать в самом начале курса, вместе с уравнениями Ньютона.

Н. Н. Бухгольц различает у д'Аламбера два рода сил инерции. Одни - силы инерции, а другие - силы инерции по д'Аламберу. В абсолютном и относительном движении это разные вещи. У д'Аламбера никакого принципа нет. Недоразумение объясняется нехорошим знанием языка. У него есть термин "сила инерции". Но понимает под этим д'Аламбер другое. Сила инерции, по д'Аламберу, - свойство, которое имеют тела; свойство, благодаря которому они "коснеют" в своем состоянии покоя или движения. Неаккуратно употребил слово "сила". В другом месте есть выражение "в силу свойства инерции". Сам принцип д'Аламбер дает без всякого упоминания силы. Он дает его для движения системы точек, а под движением д'Аламбер понимает вектор скорости. Сделано это довольно-таки туманно.

Можно рассказать принцип д'Аламбера начиная с Галилея. У него в беседах есть многократные высказывания о законе действия и противодействия, принципе эквивалентности инерционной и гравитационной масс.

Прежде чем рассказывать принцип, надо предварительно хорошо изучить биографию и научное творчество д'Аламбера. Есть неплохая книга Бертрана. Она помогает понять, как д'Аламбер пришел к своему принципу.