Клаузиус и второе начало термодинамики

Утверждение в науке первого начала термодинамики разрешило, пожалуй, меньше вопросов, чем возникло в ходе его установления. Наблюдая процессы, осуществляющиеся в газах, было замечено, что если газу предоставить дополнительный объем, то он будет самостоятельно расширяться, занимая все предоставленное ему пространство, но никогда и никому не удавалось наблюдать самопроизвольное сжатие газа. Далее, тело, нагретое до некоторой температуры, всегда охлаждается, нагревая окружающие тела и воздух, но никогда не происходит нагревания исследуемого объекта за счет охлаждения соседних тел или воздуха, хотя этот процесс не противоречит первому началу термодинамики. Или брусок, положенный на наклонную плоскость, скатывается с нее; при этом наблюдается нагревание бруска, плоскости и воздуха. Однако обратный процесс самопроизвольно не осуществляется: брусок сам по себе никогда не поднимется вверх по наклонной плоскости за счет охлаждения его и плоскости.

Приведенных примеров достаточно для того, чтобы понять сущность важнейшей проблемы термодинамики, которую ученым предстояло решить. Необходимо было разобраться в фактах и объяснить, какие из всевозможных процессов осуществимы, какие нет. Необходимо было установить, в каком направлении будет развиваться та или иная термодинамическая система, предоставленная самой себе. Но и это не все вопросы, которые волновали ученых.

Так, при работе тепловой машины Карно часть теплоты должна передаваться холодильнику. Кроме того, в реальной тепловой машине рассеяние теплоты было неизбежным фактом, что являлось причиной необратимости процессов, составляющих ее цикл. Трение, теплопроводность, теплоизлучение - все это приводило к тому, что значительная часть энергии в форме теплоты безвозвратно уходила из системы и никакими способами ее нельзя было использовать для производства работы. Теплоту, переданную холодильнику, никаким образом невозможно обратить в работу в этой же машине. Как оказалось впоследствии, проблема повышения эффективности работы тепловой машины была неотделима от сформулированных выше. Нужно было ввести какую-то количественную характеристику процессов, которая давала бы возможность оценить ту часть энергии, которая, рассеиваясь, теряет свою ценность как источник работы. Необходимо было связать ее с уже известными физическими величинами. Нужно было научиться вычислять ее для того, чтобы установить, насколько один процесс "необратимее" другого. Зная эту величину, можно было бы разрешить вопрос о том, на сколько КПД данной реальной тепловой машины меньше соответствующего значения для идеальной, работающей в том же температурном интервале. Манипулируя этой величиной, можно было бы узнать направление протекания всех мыслимых процессов и предсказать, какие из них осуществимы в реальных условиях.

Огромная заслуга Клаузиуса состоит в том, что именно ему удалось ввести в физику новую величину, названную им энтропией, использование которой давало возможность ответить на все вопросы, приведенные выше. Второе начало термодинамики представляет собой закон, который регулирует всевозможные процессы, позволяет производить оценку эффективности реальных тепловых машин и осуществляющихся в них процессах. Этот закон и был установлен Клаузиусом. Толкованию этого закона посвящена третья глава его монографии.

Содержание третьей главы не вызывает трудностей при изучении, но объем информации, заложенный в ней, очень велик и математические выкладки несколько громоздки. Попытаемся передать ее содержание современным языком, базируясь на методологических позициях нашего времени. При этом ход рассуждений ученого и его логика нисколько не пострадают.

Исходным пунктом рассуждений Клаузиуса при установлении им второго начала термодинамики служит математическое выражение для КПД идеальной тепловой машины Карно. К этому выражению можно прийти следующим образом.

Пусть рабочее тело в процессе изотермического расширения получает от нагревателя некоторое количество теплоты Q₁ и отдает холодильнику количество теплоты Q₂. Тогда работа, произведенная машиной Карно за один цикл, будет определяться разностью Q₁ - Q₂. Выражая количество теплоты и работу в одинаковых единицах, можно для КПД машины Карно в соответствии с определением записать выражение

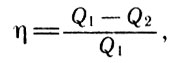
КПД

где η - КПД тепловой машины.

Так как в изотермических процессах внутренняя энергия, являющаяся функцией только температуры, неизменна ( ΔU = 0), то из первого начала следует:

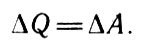
Из первого начала следует

Вычислим работу, совершаемую идеальным газом при его изотермическом расширении. В соответствии с определением работы

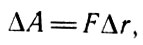
Работа

где F - сила давления газа на поршень; Δr - перемещение поршня. Так как F = pS, где р - давление газа, являющегося в этом случае рабочим телом; S - площадь поршня, то

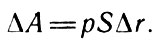
Работа (18)

Произведение SΔr представляет собой изменение объема газа под поршнем. С учетом этого выражение (18) можно представить в виде

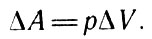
С учетом этого выражение (18) (19)

Заменяя давление идеального газа его выражением из уравнения Клапейрона для одного киломоля идеального газа

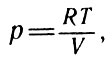
Для одного киломоля идеального газа

получим, переходя к бесконечным малым величинам:

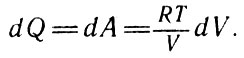
Переходя к бесконечным малым величинам (20)

После интегрирования этого выражения окончательно найдем:

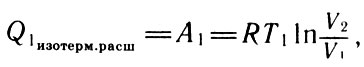
После интегрирования (21)

где Т₁ - температура нагревателя, от которого рабочее тело (идеальный газ) принимает теплоту.

Для изотермы, соответствующей температуре Т₂, выражение для работы будет иметь вид:

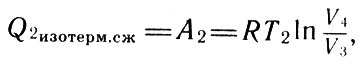
Для изотермы (22)

где Т₂ - температура холодильника, которому отдается часть количества теплоты, полученной от нагревателя. Работа при адиабатном расширении и сжатии газа в сумме даст нуль. Используя уравнение Пуассона для адиабатных процессов, можно показать, что

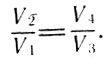
Для адиабатных процессов (23)

Тогда, подставляя выражения для Q₁ и Q₂ из (21, 22) в (17) и учитывая равенство (23), получим для КПД идеальной тепловой машины Карно выражение

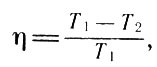
КПД идеальной тепловой машины (24)

где T₁ и T₂ - соответственно температуры нагревателя и холодильника.

Таким образом, КПД тепловой машины Карно, как это и утверждал автор, полностью определяется температурами нагревателя и холодильника.

Объединяя выражения для КПД (17) и (24), Клаузиус получает равенство, справедливое для тепловых машин, работающих по обратимому циклу:

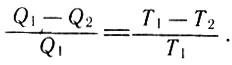
Объединяя выражения для КПД (17) и (24), (25)

После несложных преобразований получаем:

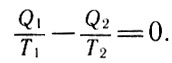
После несложных преобразований (26)

Отношение ^Q/_T Клаузиус назвал приведенной теплотой. Выражение (26) означает: для обратимого цикла, каким является цикл Карно, сумма величин, равных отношению количества теплоты, переданной или принятой каким-либо из тепловых резервуаров, к температуре соответствующего резервуара, равна нулю. Это утверждение следует из того, что приведенные теплоты, отнесенные к телу или к системе тел, принимающих теплоту, входят в уравнение (26) со знаком "минус". Иначе уравнение (26) может быть представлено в виде

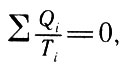
Иначе уравнение (26), (26, а)

т. е. алгебраическая сумма приведенных теплот в машине, работающих по циклу Карно, равна нулю.

В последующем изложении Клаузиус обобщает полученный результат на произвольные обратимые циклы, отличные от цикла Карно. Для этого он предлагает произвольный обратимый цикл разбить бесконечно близко расположенными изотермами и адиабатами на элементарные циклы Карно. Для каждого из элементарных циклов справедливо равенство

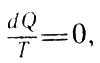
Для каждого из элементарных циклов (26, б)

где dQ - "порции" теплоты, которыми рабочее тело обменивается с нагревателем или холодильником в элементарном цикле Карно. С учетом этого для произвольного обратимого цикла имеем:

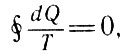
Для произвольного обратимого цикла (27)

где кружок на интеграле означает, что суммирование отношений ^dQ/_T производится по замкнутому циклу.

Введение физической характеристики тепловых процессов, представляющей собой отношение теплоты, полученной или отданной, к температуре этого перехода, оказалось очень плодотворным для дальнейшего развития термодинамики. Математически выражение (27) означает, что существует некоторая функция, изменение которой полностью определяется параметрами начала и конца процесса или цикла и не зависит от способа перехода системы из одного состояния в другое. Эта однозначная функция является важной характеристикой термодинамических процессов. На основании вышеприведенных рассуждений Клаузиус предлагает использовать для характеристики тепловых процессов эту функцию, полный дифференциал которой равен отношению ^dQ/_T, т. е.

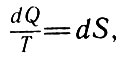
Полный дифференциал (28)

где S - искомая функция состояния, названная Клаузиусом энтропией.

Если термодинамическая система изолирована, т. е. не происходит теплообмена между телами системы и телами, не входящими в нее, то dQ=0 и для некоторого обратимого процесса 1 - 2 имеем:

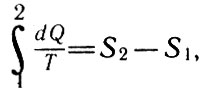
Если термодинамическая система изолирована (28, а)

или

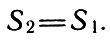
Если термодинамическая система изолирована (29)

Полученный результат означает, что в обратимых процессах энтропия системы ос тается неизменной. Иначе, L обратимых процессах повышение энтропии одних тел полностью компенсируется уменьшением энтропии остальных тел, составляющих данную термодинамическую систему. Поведение энтропии в реализуемых процессах является одним из способов определения характера данного процесса или цикла: обратимы они или нет и если необратимы, то насколько данный процесс или цикл сильнее отличается от обратимого, чем любые другие. Для того чтобы более четко уяснить сущность излагаемого, рассмотрим поведение энтропии в обратимых и необратимых процессах и циклах.

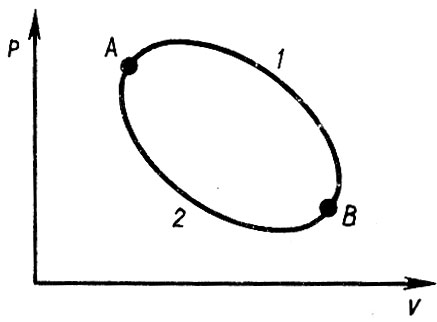
Рис. 8. Пусть некоторая термодинамическая система совершает цикл А1В2А

Пусть некоторая термодинамическая система совершает цикл А1В2А (рис. 8). Если рассматриваемый цикл обратимый, то

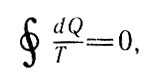
Если рассматриваемый цикл обратимый

или после разбиения этого цикла на два процесса

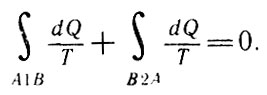
После разбиения этого цикла на два процесса

Перепишем последнее равенство в виде

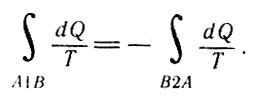
Перепишем последнее равенство (30)

Так как процессы А1В и В2А обратимые, то направление обхода В2А можно заменить на обратное и равенство (30) переписать в виде

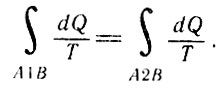
Так как процессы А1В и В2А обратимые

Следовательно, интеграл

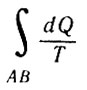
Следовательно

не зависит от пути перехода из А в В, а определяется только параметрами начального и конечного состояний.

Так как

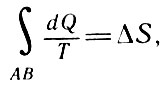
Зависимо от пути перехода

то для изолированной системы, совершающей обратимый процесс,

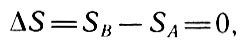
Для изолированной системы

или

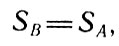
Для произвольного обратимого процесса

что и было получено выше для произвольного обратимого процесса. Полученное равенство означает, что после завершения обратимого цикла энтропия системы остается неизменной.

Иначе обстоит дело, если цикл, по которому работает тепловая машина, является необратимым. Из ранее приведенных рассуждений следует, что КПД реальной тепловой машины всегда меньше КПД машины Карно:

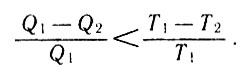
Сравнение КПД (31)

После преобразования этого неравенства получим:

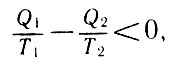
После преобразования

или с учетом правила знаков

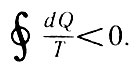
С учетом правила знаков (32)

Выражение (32) означает, что приведенная теплота, отнесенная к холодильнику, имеет большее абсолютное значение, чем соответствующая величина для нагревателя.

Рассмотрим тепловую машину, работающую по необратимому циклу. Если процесс В2А предполагать необратимым, то и весь цикл А1В2А будет также необратимым. Для этого случая

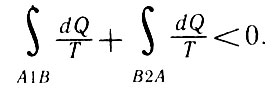
Тепловая машину, работающая по необратимому циклу

Так как первый интеграл в правой части этого неравенства записан для обратимого процесса, то его можно заменить в соответствии с (28, а):

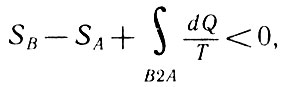
Первый интеграл в правой части можно заменить

или

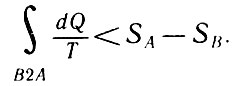
первый интеграл в правой части можно заменить

Если система изолирована (dQ=0), то для необратимого процесса получим:

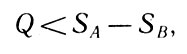
Для необратимого процесса

или

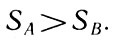
Для необратимого процесса (33)

Ввиду того что изменение состояния в системе рассматривается по направлению процесса от B к А, то можно утверждать, что к концу необратимого процесса энтропия системы возросла. Так как описываемый выше процесс рассматривался в общем виде, то отсюда следует общий вывод о возрастании энтропии в необратимых процессах. Иначе, необратимые, реальные процессы развиваются всегда в таком направлении, следование по которому приводит к возрастанию энтропии. К сказанному нужно добавить, что по приросту энтропии можно судить о степени необратимости интересующего нас реального процесса.

В этом месте у читателя возможно возникает недоумение: состояния А и В однозначно определяются параметрами системы, но они отличны, а энтропия, определяемая через эти параметры, имеет одинаковое значение и в А, и в В, если процесс обратимый, и различное, если процесс необратимый. Здесь все дело в том, что графическое изображение процессов А1В и В2А (см. рис. 8) относится к изменению состояния одного из тел термодинамической системы, в данном случае к рабочему телу тепловой машины. В действительности значение энтропии остается неизменным для группы тел, участвующих в тепловых процессах и представляющих собой термодинамическую систему (источник теплоты, источник работы, рабочее тело и др.). Повышение энтропии рабочего тела в обратимых процессах вызывает понижение ее значения в других телах системы.

Все вышеприведенные рассуждения относительно направления протекания процессов с использованием понятия энтропии и составляют сущность второго начала термодинамики. Математически второе начало термодинамики определяется следующим образом: разность энтропий двух состояний системы равна интегралу (∫_dQ/_T) между этими состояниями, если процесс между ними обратимый, и больше этого интеграла, если процесс необратимый.

Высказанные утверждения не означают, что разность энтропии между состояниями 1 - 2 зависит от типа процесса перехода между этими состояниями. Энтропия является однозначной функцией состояния термодинамической системы, и, следовательно, ее изменение для любого процесса, осуществляющегося между этими состояниями, одинаково. Знак неравенства в формуле (32) указывает лишь на то, что в случае необратимого процесса интеграл в левой части уже не выражает собой разность энтропии, а меньше ее, тогда как в обратимых процессах соблюдается равенство суммы приведенных теплот и изменения энтропии.

Второе начало термодинамики представляет собой закон, указывающий направление протекания различных процессов. Используя второе начало термодинамики, можно установить связь между тем количеством теплоты, которое превращается в работу (или получается за счет механической работы), и тем, которое переходит от более теплого тела к более холодному (или наоборот, в холодильных машинах). Существует несколько формулировок второго начала термодинамики, но все они равнозначны и приводят к одинаковым следствиям. В работе Клаузиуса второе начало термодинамики сформулировано так: "Теплота не может переходить сама собой от более холодного тела к более теплому". А несколько ниже: "Переход теплоты от более холодного тела к более теплому не может иметь места без компенсации". Эти же мысли Клаузиус выражает в виде правила: "...Дробь ^Q₁/_Q2 может зависеть только от температуры Т₁ и T₂". Последняя формулировка наиболее близка к результату, полученному Карно. Все процессы, противоречащие утверждаемому в формулировках, протекали бы с убыванием энтропии, и осуществление их практически невозможнo.

Пользуясь информацией, заложенной во втором начале термодинамики, можно теоретически исследовать всевозможные мыслимые процессы. Вычисляя изменение энтропии для интересующих нас процессов, можно узнать, обратим данный процесс или нет. Если значение энтропии в некотором процессе не изменилось, значит, данный процесс является обратимым; если же значение энтропии возросло - необратимым. Нужно отметить, что все реальные процессы протекают всегда с возрастанием энтропии. Чем больше прирост энтропии при переходе из одного состояния в другое, тем дальше данный процесс от обратимого, тем меньше работы производится за счет каждой единицы теплоты в данном процессе, тем меньше КПД данного процесса. Если расчет какого-либо задуманного процесса приводит к тому, что при его протекании энтропия должна убывать, то это означает, что такой процесс практически неосуществим. Таким образом, введение понятия энтропии дало возможность ответить на все те вопросы, которые были сформулированы в начале этого параграфа.

Понимание физического смысла энтропии связано с многочисленными трудностями, возникающими особенно у тех, кто впервые знакомится с этой физической величиной. Однако в действительности новое понятие нисколько не труднее других понятий физики. "Энтропия представляется несколько таинственной в том смысле, - пишет известный французский ученый А. Пуанкаре, - что величина эта недоступна ни одному из наших чувств, хотя и обладает действительным свойством физических величин, потому что по крайней мере в принципе вполне поддается измерению". Энтропия как физическая величина характеризует направление протекания того или иного реального процесса. Как следует из приведенных рассуждений, наиболее вероятен такой процесс, при осуществлении которого наблюдается наибольший прирост энтропии. "Энтропия является, следовательно, величиной, - продолжает Пуанкаре, - в некотором роде измеряющей эволюцию данной системы или по крайней мере указывающей направление этой эволюции".

И если до сих пор понятие энтропии приводит в смущение начинающих изучать термодинамику, то можно представить те трудности, которые стояли на пути Клаузиуса при его неустанном, хотя и нелегком, продвижении к истине. Редко кому из ученых выпадает честь ввести новую величину, характеризующую то или иное свойство. Клаузиус был одним из немногих таких "счастливчиков".