2. Эвристическое значение вариационных принципов механики

В современной физике глубокое значение имеют вариационные принципы. Трудно указать какую-либо другую область физико-математических наук, в которой столь глубоко сочетались бы абстрактные математические исследования и конкретное физическое содержание, как в вариационных принципах механики. "Вариационные принципы механики,- пишет Л. Полак,- не только великолепный инструмент научного исследования самых сложных и многогранных проблем природы и техники, но и своеобразная форма выражения законов движения, имеющая смысл далеко за пределами классической механики, в которой она возникла" (21, 780). Вариационные принципы механики неразрывно связаны с теорией групп преобразований, синтезом аналитического и геометрического аспектов механики, оптико-механическими аналогиями и единой волново-корпускулярной картиной движения, классической и квантовой теорией физических полей, вариационными методами решения задач движения, равновесия, устойчивости и структуры физических систем и другими фундаментальными проблемами.

Еще в XVII в. в геометрической оптике Ферма сформулировал вариационный принцип - принцип кратчайшего времени. Он писал, что "природа действует наиболее легкими и доступными путями, а отнюдь не более краткими" (21, 7), как это думают многие. Это положение явилось для него отправным при исследовании закона преломления света. Из оптики принцип кратчайшего времени был перенесен для решения задач в механику. В связи с тем, что при постоянной скорости принцип кратчайшего времени переходит в принцип кратчайшего пути, в механике стали пользоваться последним. В дальнейшем труды Я. и И. Бернулли, Лейбница и других подготовили необходимые условия для формулировки Мопертюи принципа наименьшего действия, который, к сожалению, видел его основание в "бесконечной мудрости творца" и целесообразности устройства Вселенной. Если у И. Бернулли и И. Ньютона представление об осуществлении законов природы простейшим путем вытекало из их убежденности в существовании причиной динамической связи, то Мопертюи доказывал универсальный характер этого принципа с помощью аргументов телеологического и теологического характера. Один из параграфов его работы "Законы движения и покоя, выведенные из метафизического принципа" называется так: "Изучение доказательств существования бога, извлеченных из чудес природы" (21, 41). Для характеристики этих теологических воззрений приведем слова Мопертюи, который, ссылаясь на Ньютона, писал: "Этот великий человек полагал, что движение небесных тел ясно доказывает существование того, что ими управляет... Множество физиков после Ньютона обнаружили Бога в Звездах, Насекомых, Растениях, Воде" (21, 42). Мопертюи утверждает, что "законы, согласно которым движение сохраняется, распределяется и уничтожается, основаны на атрибутах высшего разума" (21, 46).

Стремление Мопертюи доказать всемогущество Бога с помощью законов механики было подвергнуто очень яркой, иронической, но недостаточно глубокой критике со стороны энциклопедистов. Д'Аламбер отрицал универсальный и философский характер принципа наименьшего действия, рассматривая его только как математический принцип. Между тем как в живой, так и в неживой природе мы встречаемся с многочисленными проявлениями закономерностей, отображаемых с помощью вариационности и всеобщности, что требует философского осмысления.

Несмотря на все идеалистические и теологические выверты, точнее, вопреки им, изучая объективную действительность, Мопертюи выдвинул важный для физики принцип минимума количества действия как универсальный закон природы.

Эйлер показал, что найти выражение, которое должно быть максимумом или минимумом для каждой данной частной задачи, можно тогда, когда уже известно решение этой задачи, проведенное исходя из обычных общих принципов механики, формулирующих причинно-следственные связи явлений. Эйлер развивает и строгс научно формулирует принцип наименьшего действия в механике. В дальнейшем Лагранж показал, что принцип наименьшего действия может быть выражен в форме интеграла:

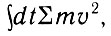
который должен иметь максимум или минимум. Принцип Лагранжа отображает причинно-следственную связь событий, он инвариантен относительно выбора координат, а потому широко используется в различных разделах теоретической физики, отображающих взаимосвязь различных видов движущейся материи, пространства-времени, и позволяет решать конкретные задачи движения для любой физической системы (непрерывная среда, гравитационное или электромагнитное поле и др.). Новая форма этому, принципу была придана в; исследованиях ирландского математика Гамильтона. По своим философским воззрениям он был близок к Беркли и Канту, но в области исследований по математике и физике он придерживался стихийно-материалистических взглядов. Он писал: "Цель физики как науки - констатировать и объяснять видимые явления, классифицировать и обобщать факты, открывать скрытое единство и постоянство природы среди видимого разнообразия и изменчивости, построить хотя бы отчасти историю внешнего мира, приспособленную к пониманию человека, дать отчет о прошлых явлениях и предвидеть будущие явления, изучать язык и истолковывать пророчества вселенной" (21, 805). Гамильтон предложил оригинальную идею: рассматривать входящий в принцип действия интеграл после его вычисления как функцию от его пределов. Введя величину Н = Т - U (Т - кинетическая энергия, U - потенциальная энергия), получившую название гамильтониана системы, он вывел свои канонические уравнения:

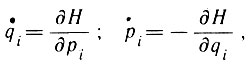
где q_i - обобщенные координаты; р_i - обобщенные импульсы, имеющие очень важное значение в физике, особенно в статистической и квантовой механике.

Гамильтон уже видел в своем принципе средство преобразования динамики и считал, что сфера его применения выходит за рамки оптики и механики. Большой вклад в развитие вариационных принципов внес и знаменитый русский математик М. Остроградский.

Между аналитической динамикой Гамильтона-Якоби и общей теорией преобразования существует внутренняя связь, которую ярко показал Софус Ли (21, 404). Его глубокая мысль состоит в том, что проблема теории возмущения по своему существу есть проблема преобразования. Оказывается, что каноническое преобразование, чрезвычайно важное в динамике, является частным случаем касательного преобразования.

Следует подчеркнуть, что внутренний синтез аналитических аспектов динамики и геометризации в n-мерных пространствах, отражая глубокое родство выражения количественных связей материального мира в анализе и геометрии, привел к такой "геометризации механики", которая в какой-то степени подготовила аналогичные, но гораздо более фундаментальные идеи теории относительности. Классическая динамика сыграла очень важную роль в дальнейшем познании действительных закономерностей материального мира.

Развитие вариационных принципов механики связано также с именем А. Пуанкаре, который в конце XIX столетия создал теорию интегральных вариантов. Он показал, что общие уравнения динамики обладают тем свойством, что они допускают линейный инвариант:

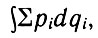
или, что естественно получается из теории Гамильтона, ∑p_idq_i - HδT. Выражение под знаком интеграла является тензором, который можно назвать тензором "количество движения - энергия". Принцип сохранения количества движения и энергии позволяет дать законам динамики форму, не зависящую от выбора координат пространства- времени, что имеет большое значение для релятивистской механики.

Крупные успехи механики в XVIII-XIX вв. порождали стремление объяснить все явления природы исходя из законов механики. Как известно, трудности, возникшие перед физикой, стремившейся свести все многообразие физических явлений к механическому движению, послужили одной из причин кризиса в физике, анализ которого дан в работе В. И. Ленина "Материализм и эмпириокритицизм". Опираясь на достижения механики, используя вариационные принципы, но не сводя все к механике, М. Планк считал, что общим принципом всех обратимых процессов является принцип наименьшего действия, который лежит в основе построения единой физической картины мира, так как он совершенно симметрично заключает в себе четыре мировые координаты и инвариантен при всех Лоренцовых преобразованиях. Планк показал, что принцип наименьшего действия применим и в термодинамике, и в электродинамике (21, 580).

Из этого краткого обзора следует, что значение вариационных принципов механики для всей физики чрезвычайно велико. Это связано с тем, что принцип Гамильтона выражает некоторое свойство, является характеристикой, общей ряду форм движения, в нем отражается то общее, что свойственно физическим формам движения, а не то, что, как утверждает ряд физиков (Г. Кирхгоф и др.), он имеет удобную для применения форму. Пользуясь аналогией, мы можем применять принцип Гамильтона не только в механике, но и в других разделах физики, в том числе и потому, что он в наиболее общей и абстрактной форме отображает сущность механической формы движения, которое в "снятом" виде входит в высшие его формы. Неразрывное, диалектико-материалистическое единство формы и содержания помогает понять методологическое значение принципа Гамильтона для всех видов движения, изучаемых физикой. То, что исторически принцип Гамильтона был выведен из уравнений динамики, т. е. из механики, и с успехом применяется в немеханических областях, не дает оснований для утверждения о механической сущности всех явлений природы¹.

¹ (Заметим, что близость принципа Гамильтона и принципа наименьшего действия не исключает и различия между ними (21, 866). )

На протяжении более чем двух столетий, прошедших со времени открытия принципа наименьшего действия, вокруг него продолжается борьба материализма и идеализма, и это, очевидно, связано с тем, что до сих пор нет глубокого, диалектико-материалистического анализа философского аспекта этого принципа. Представители религии и различных направлений идеалистической философии пытались вывести этот принцип из принципа целесообразности и экономии мышления, философы и физики-материалисты опубликовали ряд работ, в которых показали научную несостоятельность утверждений идеалистов, но фундаментальных исследований еще нет.

Следует подвергнуть дальнейшему диалектико-материалистическому рассмотрению противоречивую природу материи и движения, пространства и времени, с тем чтобы лишить мистического ореола существующую в материальном мире тенденцию, выражающуюся в том, что любая система в своем движении стремится к состоянию, которое соответствует минимуму действия. Применение законов и категорий материалистической диалектики к анализу данной тенденции, особенно закона "единства и борьбы" противоположностей, категорий симметрии и асимметрии, несомненно, принесет успех.

"В основе применения и физического смысла вариационных принципов механики,- указывал Л. С. Полак,- лежат две теоремы: теорема независимости Гильберта и теорема Эмми Нетер. Первая дает математическое обоснование вариационных принципов, вторая раскрывает их физический смысл, связывая их с центральной физической проблемой - проблемой инвариантов различных групп преобразований" (21, 863).

Вариационные принципы механики не только выражают в простой инвариантной форме уравнения движения и уравнения полей, но и заключают в себе синтез дискретного и непрерывного аспектов движения и являются выражением обобщенного принципа причинности в физике.

Немецкий математик Ф. Клейн в своей эрлангенской (60) программе впервые сформулировал принцип, согласно которому любая геометрия (элементарная, аффинная, проективная, топологическая и др.) задается системой инвариантов относительно некоторой группы преобразований; причем изоморфные группы некоторой группы преобразований, заданные на множествах различных геометрических объектов, соответствуют одной геометрии. Так, например, для Римановых геометрий основным инвариантом является скалярное произведение, заданное симметричным тензором g_ik. С другой стороны, теория непрерывных групп, развитая Софусом Ли, установила связь между интегралами дифференциальных уравнений и инвариантами непрерывных групп. Отсюда, очевидно, следует, что уравнения механики, записанные в Лагранжевом или Гамильтоновом формализме, могут быть интерпретированы в терминах непрерывной группы и ее инвариантов. (Иными словами, гамильтониан и другие константы движения, обращающие скобки Пуассона в нуль, являются инвариантами группы Ли.)

Исходя из программы Клейна можно утверждать, что геометрические свойства тел выражаются в терминах инвариантов группы, допускают изоморфную подстановку элементов пространства, в котором реализуется группа, и, следовательно, совершенно не зависят от самих геометрических объектов. Применительно к физике это означает, что различные законы сохранения интерпретируются как свойства симметрии относительно различных групп.

Современная физика имеет дело со следующими группами: группа Лоренца, заданная в пространстве Минковского, и группа непрерывных преобразований, заданная в криволинейном пространстве общей теории относительности. В релятивистской квантовой механике мы переходим от группы Лоренца к ее представлениям, определяющим преобразования волновых функций. Э. Нетер дала общий алгоритм, позволяющий найти полную систему инвариантов любой физической теории, формулируемой в терминах Лагранжева или Гамильтонова формализма. В основу этого алгоритма положена связь между инвариантами группы Ли и константами движения уравнения Гамильтона и Лагранжа. Следует, однако, иметь в виду, что развитый Э. Нетер алгоритм применим лишь к непрерывным преобразованиям; к конечным же преобразованиям он может быть применен только в тех случаях, когда эти преобразования являются частным случаем непрерывных.

Как известно, Э. Нетер получила весьма общий результат, объясняющий происхождение сохраняющихся величин и способ их получения в любой теории. Теорема, носящая ее имя, гласит: "Всякому непрерывному преобразованию координат, обращающему в нуль вариацию действия, при котором задан также закон преобразования функций поля, соответствует определенный инвариант, т. е. сохраняющаяся координация функции поля и их производных" (13, 20).

Это означает, что наличие определенных законов сохранения у материальной системы связано со свойствами материи, движением, пространством и временем, свойством симметрии, так что преобразование координат, не нарушающее симметрии системы, оставляет неизменной и функцию Лагранжа. Из этого факта следует существование определенного аддитивного интеграла движения. В применении к классической механике это приводит к следующим выводам: если материальная система изолирована или находится в постоянных внешних условиях, то функция Лагранжа не зависит явно от времени; значит, она не изменится при переходе от одного момента времени к любому следующему. В качестве следствия инвариантности функции Лагранжа по отношению к бесконечно малому изменению времени получается сохранение полной энергии системы.

Аналогичным образом бесконечно малое смещение замкнутой системы как целого не вносит никаких физических изменений в ее свойства. Из этого вытекает сохранение импульса (если же система находится в таких внешних условиях., которые не изменяются при ее смещении в определенном направлении l, то сохраняется проекция импульса системы на это направление Рl_. Используя понятие системы центра инерции и аддитивность импульса можно получить закон сохранения массы.

Наконец, закон сохранения момента замкнутой системы вытекает из инвариантности ее функций Лагранжа относительно бесконечно малых поворотов. Таким образом, из факта инвариантности системы, при сдвиге во времени, при смещении или повороте в пространстве вытекает сохранение соответствующей аддитивной величины.

Мы видим, что формально-математические операции, связанные со свойствами симметрии непрерывными преобразованиями координат, преобразованиями функции поля, являются отражением объективных свойств материи, движения, пространства и времени и наиболее общих законов сохранения, выражающих неуничтожимость материи и ее свойств. Обнаруживается органическая связь между свойствами симметрии пространственно-временной области, соответствующей данной системе, и существованием инвариантных характеристик у этой материальной системы. В законах сохранения энергии, импульса, момента количества движения отражаются однородность времени, однородность и изотропность пространства. Это было новое подтверждение всеобщности указанных законов. Однако это не означало, что наиболее общие черты пространства и времени определяют конкретные особенности движения данной системы, ибо сохранение какой-либо динамической величины может обеспечиваться бесчисленным количеством конкретных способов движения.

В конечном счете свойства пространства и времени определяются, несомненно, свойствами материи, характером ее движения, и потому не существует плоского пространства в строгом смысле этого слова; в больших космических масштабах пространство - время "искривляется" благодаря наличию гравитирующих масс, его свойства зависят также и от космических электромагнитных полей, образованных движением заряженных частиц; в микроскопических масштабах пространство и время, судя по многим данным, также не являются однородными и изотропными.

Тем не менее абстрактное понятие однородного и изотропного пространства и времени во многих случаях можно считать очень хорошим приближением к действительности, и тогда поведение материальных объектов, находящихся в таких областях пространства и отрезках времени, будет адекватно описываться с помощью соответствующих законов сохранения.